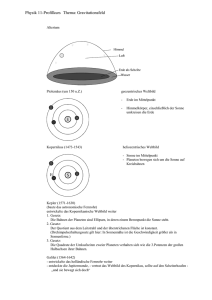
m r m G r mm GF = = 805.9 mg m s m = =

100
101
Beispiel: Mond
6. Gravitation
rM = 1738 km
Gravitationswechselwirkung: eine der vier fundamentalen Kräfte
(die anderen sind elektromagnetische, schwache und starke
Wechselwirkung)
m2
r
Ein Körper mit Masse m2 im Abstand r zu einem Körper mit
Masse m1 übt auf diesen ein Kraft aus von:
r
m1
F1
m2
F2
( F2 = − F1 )
mm
F1 = −G 1 2 2
r
r
r
gM = G
mM
m 1
=
1
.
6
2
 s 2  ≈ 6 g
rM
Mond (mM)
Die Gravitationsbeschleunigung ist auf der Mondoberfläche etwa
sechsmal kleiner als auf der Erdoberfläche.
G: Gravitationskonstante
G = 6.67 10-11 Nm2/kg2
Auf Masse m2 wirkt die gleiche Kraft in umgekehrter Richtung.
Bem.: hierbei wurde verwendet, dass das Gravitationsfeld
außerhalb einer homogenen Kugel identisch ist zum
Feld der im Kugelzentrum vereinigten Kugelmasse
Eigenschaften der Gravitation:
Beispiel: Erde
rE = 6378 km
m2
r
Erde (mE)
mM = 7.35 1022 kg
mE = 5.98 1024 kg
• auschließlich attraktiv (es gibt keine „negativen“ Massen)
• kann daher nicht abgeschirmt werden
m m
m
F = G E 2 2 = G E2 m2
rE
rE
• ist die schwächste der 4 Fundamentalwechselwirkungen
m
= 9.805  2  m2 = g m2
s 
• ist die stärkste über kosmische Distanzen wirkende WW
Erdbeschleunigung g = 9.81 m/s2 gilt nur auf der Erdoberfläche!
(nimmt quadratisch ab mit dem Abstand zum Erdmittelpunkt)
(die Gravitations-WW zwischen Elektronen und Protonen ist
1040 mal schwächer als die Coulomb-WW !)
( wegen der 1/r2 – Abhängigkeit und der fehlenden Abschirmung)
102
103
Damit:
6.1. Gravitationspotential
V(r)
V(r)
Wir betrachten das Gravitationsfeld einer Punktmasse m am Ursprung
(die auf einen Probemasse mp am Ort r ausgeübte Kraft).
Die potentielle Energie im Gravitationsfeld ist
Gm
V (r ) = −m p r
r
E pot = W = − ∫ F (r ')dr '
Potential des Gravitationsfelds
einer Punktmasse
r0
Potential: potentielle Energie, hier mit
r0 → ∞
(das Potential im Unendlichen wird auf Null gesetzt)
Es gilt wie immer:
F = −∇V ( r )
r
V (r ) = − ∫ F (r ')dr '
Bem.: ähnlich wie das elektrostatische Potential auf die Ladung
wird manchmal das Gravitationspotential auf die Masse
des Probekörpers normiert.
∞
Bei radialem Integrationspfad (
r

m m
V (r ) = − ∫  −G p 2 
r' 
∞
F dr '
):
r
mp m
r' dr ' = ∫ G 2
r'
r'
∞
r' dr '
r'
Das Potential hängt also nur vom Betrag des Abstands ab:
r
V (r ) = ∫ G
∞
mpm
r'
2
dr ' = − m p
Gm
r
1
Gm
Vg (r ) =
V (r ) = − mp
r
Dann ist die Gravitationsbeschleunigung:
g = −∇Vg (r )
rr
104
6.2 Planetenbewegungen
Bewegung der Planeten im Gravitationsfeld der Sonne
(Beschreibung gilt allgemein für die Bewegung von Körpern in
einem Zentralkraftfeld)
105
0 < e <1
⇒
r
p
p
≤r≤
1+ e
1− e
b
a
Ellipse
a=
Es gelten die Kepler‘schen Gesetze (1619):
Die Planeten bewegen sich auf Ellipsen-Bahnen. Die
Sonne befindet sich in einem der Brennpunke der Ellipse
2. Die Verbindungslinie Sonne-Planet überstreicht in gleichen
Zeiten gleiche Flächen
3. Die Quadrate der Umlaufzeiten verhalten sich wie die
Kuben der großen Halbachsen der Ellipsen
p
p
;
b
=
1 − e2
1 − e2
1.
Zu 1:
Man kann zeigen, dass die Bahnen von Körpern
in einem 1/r-Potential immer Kegelschnitte sind,
die sich in Polarkoordinaten beschreiben lassen durch
p
r=
1 + e cos ϕ
e =1
⇒
e >1
⇒
r
r≥ p/2
Parabel
r ≥ p / (1 + e)
Hyperbel
r
a=
ϕ
p und e sind Parameter, die die Form der Kurve bestimmen
Fälle:
e=0
⇒
r=p
r
(Kreisbahn)
b/2
a/2
p
p
;b=
e −1
e2 − 1
2
⇒ alle geschlossene Bahnen sind Kreise oder Ellipsen
Zu 2:
Es gilt Drehimpulserhaltung
l = r × p = konst.
106
in beiden Fällen (falls
v α
r
Planet
Sonne
Fläche dA
107
Die in der Zeit dt überstrichene
Fläche ist
1 r v dt sin α
2
1 1 r × mv
= r × v dt =
dt
2
2 m
1 ldt
2m
):
mS mP
r2
m
ω 2 = G 3S
r
mP rω 2 = G
dA =
=
mS >> mP
Die Umlauffrequenz ist unabhängig von mP !
Mit
ω=
2π
τ
 2π  = G mS
 
r3
 τ 
2
wird dies zu:
Also:
τ2 =
Da der Drehimpuls (und die Masse) konstant sind,
ist auch dA/dt konstant!
4π 2 3
r
GmS
Betrachten Planet auf Kreisbahn (einfachster Fall)
Zu 3:
Zahlenwerte: Bahnradien und Umlaufzeiten
v = rω
r
Fg
mS
mp
Sonnenmasse: mS = 1.99 1030 kg
Es gilt:
Zentripetalkraft = Gravitationskraft
(ruhender Beobachter)
Zentrifugalkraft = -Gravitationskraft
(mitbewegter Beobachter)
Erde
r = 149.6 109 m
τ = 365d
Merkur
r = 57.9 109 m
τ = 88 d
Jupiter
r = 778 109 m
τ = 11.6a
Pluto
r = 5910 109 m
τ = 249a
108
6.3 Schwerpunktsystem
109
Vereinfachung des Problems:
Bisherige Behandlung gilt nur näherungsweise (für die Bewegung
einer Masse um eine sehr viel größere Masse); tatsächlich
kreisen zwei sich gegenseitig anziehende Körper um ihren
gemeinsamen Schwerpunkt.
Dann ist:
m1
r1s
r 2s
r = r2 s − r1s
Definiere Koordinate
(Abstand der
Körper)
m m r 2s = − 1 r1s = 1 (r − r 2s )
m2
m2
Schwerpunkt:
m2
rS
m1r1 + m2 r2
rS =
m1 + m2
r 2s =
⇒
m1 r
m1 + m2
Damit wird das Kräftegleichgewicht:
Relativkoordinaten im Schwerpunktsystem:
r 2s = r2 − rS
r1s = r1 − rS
Hierfür gilt:
m1r s + m2 r 2s = 0
(der Schwerpunkt im Schwerpunktsystem liegt im Ursprung)
Damit lauten die Kräftegleichgewichte:
mm
m1 r1 S ω 2 = G 1 2
r1S + r2S
2
mm
m2 r2S ω 2 = G 1 2
r1S + r2S
2
m1m2 2
mm
r ω = G 1 2 2
m1 + m2
r
Hat die Form eines Ein-Körper-Problems
ma = F
wenn man die „effektive“ Masse einführt:
µ=
m1m2
m1 + m2
Hiermit erhält man:
mm
r
µ r ω 2 = G 1 2 2
Damit ist das Zwei-Körper-Problem (zwei Massen kreisen
umeinander) auf ein Ein-Körper-Problem (eine Masse kreist
in einem Zentralkraftfeld) zurückgeführt worden!
110
Die Kreisfrequenz der Bewegung der beiden Körper
umeinander ist also
ω2 =
111
ω2 = G
Kreisfrequenz:
mm
m +m
G 1 3 2 = G 1 3 2
µ
r
r
1
ω = 2.67 *10−6 1/s , τ = 27 d
⇒
Die zuvor angegebene Formel für die Kreisfrequenz gilt nur
für sehr ungleiche Massen; bei ähnlichen Massen ist sie
größer!
Auf der Erde wirken die Gravitationskraft des Monds sowie
Trägheitskräfte.
Annahme: das Gravitationsfeld des Monds sei homogen, d.h. es
gelte überall
m g M = G M3 r
r
6.4 Gezeiten
Körper in einem inhomogenen Gravitationsfeld erfahren
Gezeitenkräfte.
Wir betrachten das System Erde-Mond (Usprung im Erdmittelpkt.)
Erdradius:
Erde
rO
r
Mond
r = 384000 km
mE = 5.98*10
Schwerpunkt:
⇒
r0 = 6378 km
Die Beschleunigung auf der Erdoberfläche ist dann (im
rotierenden System:
rO
m
ages = − g + G M2
rO
r
r − ω × (ω × ( rO − rS ) )
r
Abstand Erde-Mond:
rS
Massen:
mE + mM
3
r
24
kg
mM = 7.35*10
mM mE 0 + mM r
rS =
=
r
mE + mM
mE + mM
rS = 4662 km
Gravitation
Erde
Gravitation
Mond
Zentrifugalbeschleunigung
Wegen der Wahl des Koordinatensystems gilt::
22
kg
ω ⊥ rS
⇒
ω × (ω × rS ) = −ω 2 rS
Für Orte auf der Erdoberfläche in einer Ebene senkrecht
zur Drehachse gilt ebenfalls:
ω ⊥ rO
⇒
ω × (ω × rO ) = −ω 2 rO
112
Aber: das Gravitationsfeld des Monds ist nicht homogen! Die
Abweichung vom mittleren Feld führt zu einer Otsabhängigkeit
der Beschleunigung auf der Oberfläche.
Damit wird die Beschleunigung:
rO
m
ages = − g + G M2
rO
r
Mit
ω 2 rS = G
113
r
2
2
+ ω rO − ω rS
r
Abweichung:
mE + mM mM mM 3 m +m r =G 3 r
r
r
E
M
Hängt von der Richtung von
rO
ages = − g + ω 2 rO
rO
wird dies:
m
m ∆g M = G M 3 ( r − rO ) − G M3 r
r − rO
r
Erde
rO ab!
rO
r − rO
r
Zwei einfache Fälle:
Im Falle eines homogenen Gravitationsfelds
des Monds
rS
wäre die Beschleunigung auf der Erdoberfläche in der Ebene
senkrecht zur Drehachse überall gleich groß und radial
ausgerichtet!
Anders ausgedrückt: die ortsabhängige Zentrifugalbeschl.
und das homogene Gravitationsfeld addieren sich (in dieser
Ebene) zu einem rotationssymmetrischen Feld.
1.
⇒
+
rO r
gM
rO
3
r
⇒
r − rO = r ± rO
( „+“ für mondabgewandte Seite)
⇒
aZf
r 
3  ≈ −GmM
r 
Zeigt zum Erdmittelpunkt!
rS
aZf + g M
r − rO ≈ r
⇒
 r − rO
∆g M = GmM  3 −
 r − rO
2.
rS
rO ⊥ r
r
r − rO = r ± rO r
114
Damit:
 r ± rO
∆g M = GmM 
 ( r ± r )3
O

r
= GmM r
Führt auf der Erde zu Wasserbergen und –tälern:
r
r 

−
r r 3 
Erde
Mond

1
1
− 2

2

 ( r ± rO ) r 
≈
1
 r 
r 2 1 ± O 
r

2
≈
1
r 

r 2 1 ± 2 O 
r

≈
r 
1
1∓ 2 O 
2 
r 
r
r
≈ GmM r
rO 1 
1
 2 ∓2 3 − 2
r r 
r
rO r
= ∓2GmM 3 r r
( „-“ für mondabgewandte Seite)
Resultat:
∆g M
rS
rO
2GmM 3
r
rO
−GmM 3
r
Zwei Wasserberge!
Die Erde rotiert schneller als das System Erde-Mond
⇒ die Wasserberge wandern, Ebbe und Flut wechseln im
Abstand von 6 h
rO
∆g M ≈ 2GmM 3
r
also
115
Gesamtunterschied:
3GmM
rO
≈ 1.7 *10−7 g
3
r