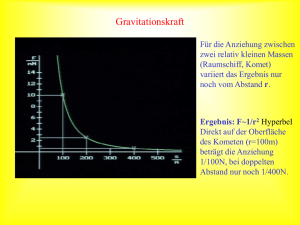
Gravitationsfeld

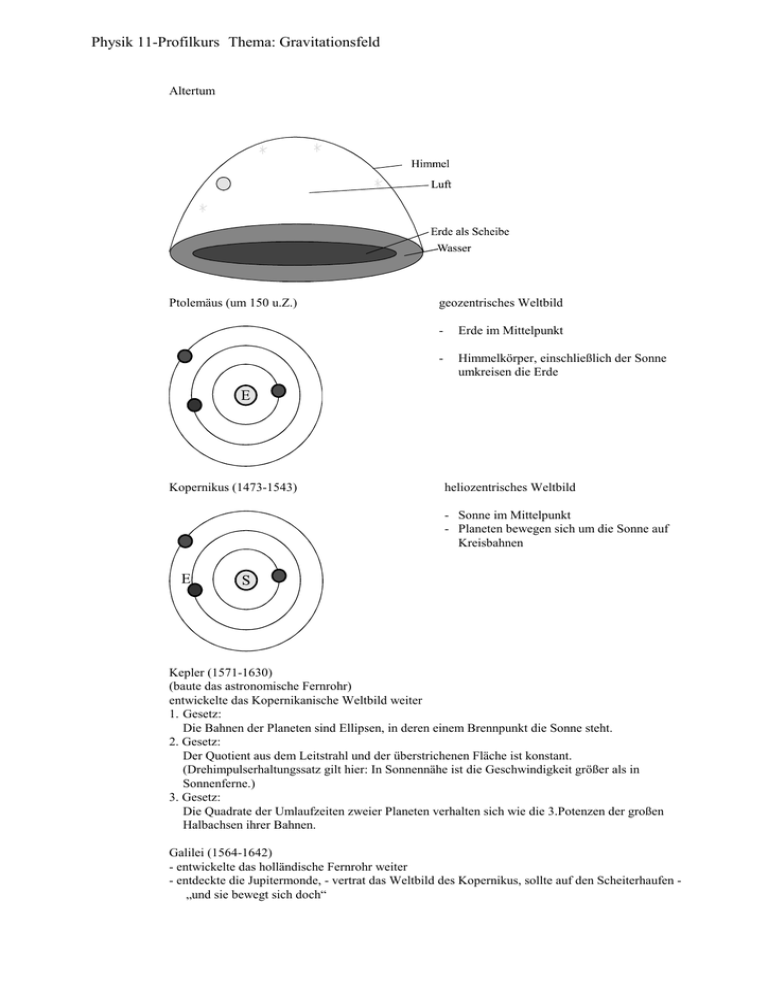
Physik 11-Profilkurs Thema: Gravitationsfeld
Altertum
Ptolemäus (um 150 u.Z.)
Kopernikus (1473-1543)
geozentrisches Weltbild
-
Erde im Mittelpunkt
-
Himmelkörper, einschließlich der Sonne
umkreisen die Erde
heliozentrisches Weltbild
- Sonne im Mittelpunkt
- Planeten bewegen sich um die Sonne auf
Kreisbahnen
Kepler (1571-1630)
(baute das astronomische Fernrohr)
entwickelte das Kopernikanische Weltbild weiter
1. Gesetz:
Die Bahnen der Planeten sind Ellipsen, in deren einem Brennpunkt die Sonne steht.
2. Gesetz:
Der Quotient aus dem Leitstrahl und der überstrichenen Fläche ist konstant.
(Drehimpulserhaltungssatz gilt hier: In Sonnennähe ist die Geschwindigkeit größer als in
Sonnenferne.)
3. Gesetz:
Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die 3.Potenzen der großen
Halbachsen ihrer Bahnen.
Galilei (1564-1642)
- entwickelte das holländische Fernrohr weiter
- entdeckte die Jupitermonde, - vertrat das Weltbild des Kopernikus, sollte auf den Scheiterhaufen „und sie bewegt sich doch“
Das Gravitationsgesetz
Wovon hängt der Betrag der Kräfte ab?
Vermutung:
M, m, r
Gesucht ist eine Gleichung F = f (M, m, r)
Herleitung des Gleichung:
F1 = m · ω2 · r
F1 = m
F1 = m
4π 2 ⋅ r
3
T2
4π 2 r
r3
F1 = C1 ⋅ m
2
r1
T
= 12 (3. Kepler’sches Gesetz)
3
r
T
3
r
= const. = C
T2
r3
T2 =
C
⋅C
4π 2 r
F2 = C 2 ⋅ M
r3
4π 2 r
r3
4π 2
4π 2
=
C
⋅
M
2
r2
r2
C1m = C 2 M
C1 ⋅ m
C1 ~ M
C1 = C'⋅M
F1 = C'⋅M ⋅ m
F= γ⋅
4π 2
r2
M⋅m
r2
C'4π 2 = γ
Gravitationsgesetz (Newton 1686)
F ... Gravitationskraft
γ ... Gravitationskonstante (γ = 6,67 · 10-11 Nm2kg-2)
M, m ... Masse der beiden Körper
r ... Abstand der Schwerpunkte der Körper
Anwendungen zum Gravitationsgesetz
1. Bestimmung der Masse der Erde
Gravitationskraft eines Körpers auf der Erdoberfläche:
F=γ
m1m e
me =
Fre
m1 γ
me =
m1gre
m1 γ
me =
gre
γ
re
2
2
2
2
m e = 5,97 ⋅ 10 24 kg
2. Berechnung der 1. kosmischen Geschwindigkeit
(Kreisbahngeschwindigkeit)
Fr = Fgrav
m ⋅ me
mv 2
=γ
2
re
re
γ ⋅ me
re
v=
v = 7,9
km
s
3. Bestimmung der Masse der Sonne
Erde umkreist die Sonne
Fr = Fgrav
meω 2 r = γ
me ms
r2
ω r
ms =
γ
2 3
ms =
4π 2 r 3
T2 γ
m s = 1,99 ⋅ 10 30 kg
Übung
Berechne die Bahngeschwindigkeit eines Satelliten, der die Erde in 1000 km Höhe umkreist!
Gib die Umlaufzeit an!
Fr = Fgrav
m ⋅ me
mv 2
=γ
r
r2
γm e
v=
r
v = 7,4 kms-1
T = 105 min
Bestimmung der Gravitationskonstanten nach Cavendish 1798
dynamische Methode
Ablauf:
1. Kugeln in Extremlage bringen
2. Kugeln in andere Extremlage
bringen
3. Beschleunigung des Lichtzeigers
bestimmen durch Weg- und
Zeitmessung
d = 0,05m
r = 0,0456m
e = 8,05m
M = 1,5kg
t = 105s
x = 0,1m
Torsionspendel in Extremlage
2Fgrav = 2γ
mM
r2
mM
Wegdrehen der großen Kugeln in
andere Extremlage (gleichmäßige
Beschleunigung)
4Fgrav = 4γ
Weg des Lichtzeigers
s d
=
x e
2
Herleitung:
F = 2ma = 4 γ
γ=
r
s=
Gravitationskraft + rücktreibende
Kraft des Torsionsdrahtes
2
d⋅x
2⋅e
ähnliche Dreiecke
mM
r2
ar 2
2M
a=
2s
t2
2sr 2
d⋅x
s=
2
2⋅e
t 2M
2
d⋅x⋅r
γ=
2⋅ t2 ⋅e⋅ M
γ=
Ergebnis des Experimentes mit der
Gravitationsdrehwaage von Leybold:
γ = 4,06 ⋅ 10 −11
m3
kgs 2
statische Methode
Ablauf:
1. Ermittlung der Schwingungsdauer
2. erste Extremlage markieren
3. zweite Extremlage markieren und x
messen
4. Berechnung
d = 0,05m
r = 0,0456m
e = 8,05m
M = 1,5kg
T = 592s
x = 0,13m
M grav = M tor
T = 2π
J
D
2 ⋅ Fgrav ⋅ d = D ⋅ ϕ
mM
4π 2 2md 2
⋅
d
=
ϕ
r2
T2
M
4π 2 d 2
x
tan(2ϕ) =
γ 2 ⋅d =
ϕ
2
e
r
T
2 2
M
4π d x
γ 2 ⋅d =
⋅
2e
r
T2
2
2
2π dxr
γ=
T 2 eM
D=
4π 2 J
T2
D=
J = 2md 2
4π 2 2md 2
T2
2γ
für kleine Winkel : 2ϕ =
x
e
ϕ=
x
2e
Ergebnis des Experimentes mit der Gravitationsdrehwaage von Leybold:
γ = 6,6 ⋅ 10 −11
m3
kgs 2
Weitere Methode zur Bestimmung der Gravitationskonstanten jedoch mit höherem technischen und
rechnerischem Aufwand:
Richardz und Krigar-Menzel 1896 in den Spandauer Kasematten in Berlin,
Bleiklotz mit 2 m3 Volumen
Verschiebungsarbeit im Gravitationsfeld und Gravitationsfeldstärke
Verschiebungsarbeit im Gravitationsfeld
Begriff des Gravitationsfeldes:
Der Raum, in dem an jedem Punkt auf einen dorthin gebrachten Körper allein aufgrund seiner
Masse eine Kraft, die Gravitationskraft, ausgeübt wird, bezeichnet man als Gravitationsfeld.
Ein Körper der Masse m soll im Gravitationsfeld des Zentralkörpers der Masse M vom Abstand r1 auf
den Abstand r2 verschoben werden.
Weil die Kraft nicht konstant ist, sondern mit wachsendem Abstand kleiner wird, kann die Gleichung
für die Hubarbeit W = FG ⋅ ∆h nicht benutzt werden.
∫
r2
W = F(r )dr
r1
∫
r2
W= γ
r1
mM
dr
r2
mM r2
|
r r1
mM
mM
W = −γ
− (− γ
)
r2
r1
1 1
W = γmM ( − )
r1 r2
W = −γ
Die Verschiebungsarbeit ist unabhängig vom Weg. Sie ist nur vom Anfangs- und
Endpunkt abhängig.
Herleitung der 2. kosmischen Geschwindigkeit
m 2
1 1
v = γmm E ( − )
2
rE r2
m 2
1
v = γmm E
2
rE
v=
2 ⋅ γ ⋅ mE
rE
v = 11,2
km
s
r2 → ∞
Die Gravitationsfeldstärke G *
An einem bestimmten Ort ist die Kraft auf den Körper der Masse m proportional zu m.
F~m
F = c⋅m
F
c=
m
Der Proportionalitätsfaktor c wird Gravitationsfeldstärke genannt und erhält das Formelzeichen G*.
G* =
F
m
Die Gravitationsfeldstärke entspricht der Fallbeschleunigung am jeweiligen Ort.
Die potentielle Energie im Gravitationsfeld der Erde
m
M
8
Erde
r
1
r2
Verschiebt man den Körper von r1 nach r2, so steigt seine potentielle Energie um ∆Epot.
1 1
− ) = ∆E pot
r1 r2
1 1
W = − γ ⋅ m ⋅ M ⋅ ( − ) = ∆E pot
r2 r1
m⋅M
E pot = − γ ⋅
r
W = γ⋅m⋅M ⋅(
Verschiebungsarbeit = Änderung der potentiellen Energie.
Wo legt man das Nullniveau hin?
E pot = 0 liegt im Unendlichen. Befindet sich ein Körper im Gravitationsfeld eines Zentralkörpers, hat
er negative potentielle Energie.
Begründung für diese Festlegung:
Erteilt man einem Körper (Rakete) kinetische Energie, so wird der Körper immer langsamer, gewinnt
dafür an Höhe. Befindet sich der Körper im Unendlichen und ist die gesamte kinetische Energie
aufgebraucht, hat er die Gesamtenergie Null.
Das ist sinnvoll, denn der Körper wird nicht mehr angezogen und bewegt sich nicht mehr.
Hat der Körper im Unendlichen noch kinetische Energie, ist seine Gesamtenergie größer als Null.
E pot ~ −
E ges = E kin + E pot
E ges =
m ⋅ v2
m⋅M
−γ⋅
2
r
1
r
Die kosmischen Geschwindigkeiten
1. kosmische Geschwindigkeit
(Kreisbahngeschwindigkeit) v I = 7,9
km
s
Der Raumflugkörper bewegt sich auf einer
Kreisbahn unmittelbar über der Erde. Liegt die
Geschwindigkeit zwischen 1. und 2. kosmischer
Geschwindigkeit, ist die Bahn elliptisch.
2. kosmische Geschwindigkeit
(Parabelgeschwindigkeit) v II = 11,2
km
s
Der Raumflugkörper verlässt das Gravitationsfeld
der Erde von der Erdoberfläche startend auf einer
Parabelbahn.
3. kosmische Geschwindigkeit
(Hyperbelgeschwindigkeit) v III = 16,7
km
s
Der Raumflugkörper verlässt unser Sonnensystem
von der Erde startend auf einer Hyperbelbahn.