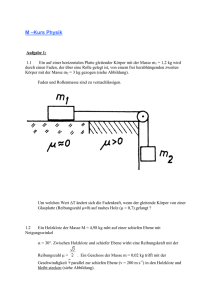
6. Gravitation 1687 publizierte Newton das Gravitationsgesetz. In
Werbung

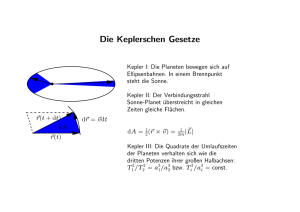
6. Gravitation 1687 publizierte Newton das Gravitationsgesetz. In Kapitel 2.1 haben wir die Äquivalenz von träger und schwerer Masse besprochen: mT mS Jede Masse besitzt die Fähigkeit, radialsymmetrisch um sich herum ein Zentralkraftfeld auszubilden und damit eine anziehende Wechselwirkung auf die Umgebung auszuüben, ganz gleich, ob ein Wechselwirkungspartner vorhanden ist oder nicht. Die Feldstärke dieses so genannten Gravitationsfeldes berechnet sich wie folgt: E M r r2 r (1) : Gravitationskonstante = (6,6720+0,0004) .10-11 Nm2 / kg M : (Erd-)Masse r : Abstand von der felderzeugenden Masse 6.1. Gravitationsgesetz Tritt nun eine zweite Masse in das Feld der ersten, wirkt auf beide die Gravitationskraft. FG m1m2 r r2 r (2) An der Erdoberfläche (r rE ) wirkt auf jeden Körper die Gewichtskraft G m g . Demzufolge ist auf der Erdoberfläche: g M rE 2 (3) Die Fallbeschleunigung g ist nichts anderes als die Gravitationsfeldstärke E(rE) an der Erdoberfläche. Newton selbst kannte 𝝲 noch nicht; wie kam er zu „seinem“ Gesetz? Beobachtung: Die Erde zieht einen bestimmten Körper mit einer Kraft an, die proportional zu deren Masse ist, also F m. Aus dem Reaktionsprinzip folgerte er: F MErde. Es folgt also schon mal: F m* MErde. Andererseits muss diese Kraft mit zunehmendem Abstand abnehmen: F rn. Zwischenergebnis: F m* MErde/ rn Zur Bestimmung von n verglich er die Anziehung eines Körpers an der Erdoberfläche mit der des M E mK M m FM E n M mK g mM a (*) n rE rM Mondes: FK a: Zentripetalbeschleunigung, die den Mond auf seine Erdumlaufbahn (fast Kreisbahn) zwingt. 2 2 2 m m 6,37 106 60 2 2, 7 103 2 a = 𝟂2r = s s TM 27,3 86.400 2 Der Abstand des Mondes von der Erde beträgt ungefähr 60 Erdradien; die Umlaufzeit des Mondes um die Erde etwa 27,3 Tage (knapp 1 Monat). Aus Gl. (*) folgt g FM ME ME . ;a n rE rM n Der Quotient g / a = 3.600 liefert n = 2. Also fällt die Gravitationskraft mit 1 / r2 ab. Cavendish hat mittels einer Drehwaage 1797 die Masse der Erde sehr präzise bestimmt: ME = 5,98.1024 kg. 6.2 Die Kepler‘schen Gesetze der Planetenbewegung 1. Kepler'sches Gesetz (1609): Die Planeten umlaufen auf Ellipsenbahnen die Sonne, die in deren gemeinsamem Brennpunkt steht. Perihel (Sonnennähe) Planet Sonne P Aphel (Sonnenferne) A F1 2. Kepler‘sches Gesetz (1609): Der von der Sonne zum Planeten gezogene Radiusvektor überstreicht in gleichen Zeiten t gleiche Flächen A. t r S P A Experiment: Indischer Seiltrick: A dA A t const. t dt (4) 3. Kepler‘sches Gesetz (1619): Die Quadrate der Umlaufzeiten T1 und T2 zweier Planeten verhalten sich wie die Kuben der großen Halbachsen a1 und a2. P1 T12 a13 T2 2 a23 (5) a1 P2 S a2 zum 2. Kepler-Gesetz Dreieck v(t+dt) P2 Ellipsenbogenelement (A‘) r(t+dt) v t dt sin v(t) S r(t) dA – A(Dreieck SP1P2) + A‘(Ellipsenbogenelement) r vdt sin P1 1 2 Null für dt 0 1 r v sin dt 2 dA 1 1 r mv sin dt 2 m dA 1 rp 2m 1 L konst. , da L konst. 2m Bahnkurve 6.3. Die Kosmischen Geschwindigkeiten Die 1. Kosmische Geschwindigkeit ist diejenige, die ein Körper (genau) haben muss, um auf einer Kreisbahn die Erde umrunden zu können. In diesem Falle ist die Gravitationskraft die Radial- bzw. Zentripetalkraft (Kräftegleichheit). Betragsmäßig gilt: mM mv 2 2 mr r2 r ME rE h v2 r rE h v1 2 M E r (6) Die 2. Kosmische Geschwindigkeit ist diejenige, die ein Körper mindestens haben muss, um das Gravitationsfeld der Erde verlassen zu können. Er muss also genügend kinetische Energie besitzen, um das Gravitationspotential (der Erde) zu überwinden. mM m 2 v r 2 v2 2 M E r (7) Setzt man in Gleichung (7) für die Erd- die Sonnenmasse ein, erhält man die 3. Kosmische Geschwindigkeit, die ausreicht, das Sonnensystem zu verlassen. Setzt man in Gleichung (7) für M E die Masse superschwerer schwarzer Löcher ein und für v die Lichtgeschwindigkeit c , so erhält man aus Gleichung (7) den so genannten Schwarzschildradius, aus dessen Innerem auch keine Photonen entweichen können. Anmerkungen zum Gravitationspotential: Man kommt von der Gravitationskraft zum Potential, indem man entlang des Weges integriert (Weg- oder Linienintegral). Die Integrationsgrenzen des (bestimmten) Integrals werden dabei so gelegt, dass vom Ort r bis nach Unendlich integriert wird, weil dort, in ausreichendem Abstand also, das Potential verschwindet.