Die Keplerschen Gesetze

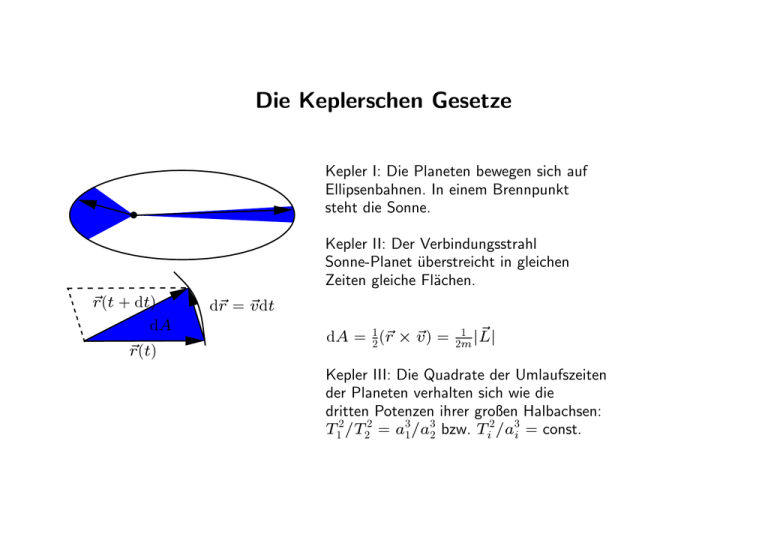
Die Keplerschen Gesetze
Kepler I: Die Planeten bewegen sich auf
Ellipsenbahnen. In einem Brennpunkt
steht die Sonne.
Kepler II: Der Verbindungsstrahl
Sonne-Planet überstreicht in gleichen
Zeiten gleiche Flächen.
~
r (t + dt)
dA
~
r (t)
d~
r=~
v dt
dA = 12 (~
r×~
v) =
1 ~
2m |L|
Kepler III: Die Quadrate der Umlaufszeiten
der Planeten verhalten sich wie die
dritten Potenzen ihrer großen Halbachsen:
T12/T22 = a31/a32 bzw. Ti2/a3i = const.
Die Gravitation
Newton hat erkannt, dass die Keplerschen Gesetze aus derselben Kraft folgen, die
auch Äpfel im Fallen beschleunigt. Die Gravitation wirkt zwischen zwei Körpern
mit Massen m1 und m2.
Aus Kepler I und II bzw. der Drehimpulserhaltung folgt, dass es sich dabei um
ein zentrales Kraftfeld handeln muss.
F~ (~r) = f (r)~r̂
Feld: An jedem Punkt im Raum ist eine Größe zugeordnet, z. B. die Temperatur
−→ Temperaturfeld. Ist jedem Punkt ein Vektor zugeordnet, wie z. B. die Gra-
vitationskraft, so handelt es sich um ein Vektorfeld. Ein Temperaturfeld ist ein
skalares Feld.
Die Gravitationskraft wirkt proportional zur Masse eines Körpers, die Gravitation
muss ferner, nach Newton III, gleich stark auf Körper 1 wirken, wie auf Körper 2
(“actio = reactio”), also
F~G = Gm1m2f (r)~r̂,
wo G ≈ 6, 673(10) · 10−11m3 kg−1 s−2 die schwierig zu bestimmende Gravitationskonstante ist.
Entlang einer Planetenbahn wirkt die Gravitation als Zentripetalkraft, sie h ält den
Planeten auf seiner Bahn (beschleunigte Bewegung!)
GmiM¯f (ri) = miωi2ri.
Aus Kepler III haben wir ωi2 ∝ Ti−2 ∝ ri−3 und folglich f (ri) ∝ ri−2
m M¯ ~r
F~G(~r) = −G
r2 |~r|
Messung von G mit der Drehwaage von Cavendish
M2
m1
Spiegel
m2
Spiegel
M1
m1 = m 2
Skala
Laser
M1 = M 2
d4
Verdrillung des Fadens: Drehmoment M = π2 G∗ 16
lφ
Skala
Laser
Gleichgewicht des rücktreibenden Drehmomentes M und des durch die Gravitation
ausgeübten Drehmomentes MG = 2FGL, wo
µ
mM
4π
FG = G 2 = G
r
3
¶2
ρ2ri3Ri3.
Die Gravitationskonstante kann nun ermittelt werden:
µ
4π
G
3
¶2
ρ2ri3Ri3
=
G =
1 π ∗ d4
G
φ
2L 2 16l
9G∗ r2(d/2)4
φ
64π lLρ2ri3Ri3
wo G∗ das Torsionsmodul des Fadens ist (siehe später).
Bestimmung von g
φ0
φ
Bewegungsgleichung
mg sin φ = −mLφ̈
L
L cos φ
m
L(1 − cos φ)
m~g
Lösen durch Reihenentwicklung von sin φ
sin φ ≈ φ −
φ3
3!
und Vernachlässigen der höheren Terme
bei kleinem φ. Damit
mgφ = −mLφ̈,
p
¡p g ¢
Schwingungsgleichung φ(t) = A sin
L t mit Schwingungsdauer T = 2π L/g.
Potentielle Energie im Gravitationsfeld
Wir können einfach die potentielle Energie einer Masse m im Gravitationsfeld
einer Masse M berechnen. Die Arbeit A, die erforderlich ist, um einen Körper
vom Abstand r0 in einen Abstand r1 zu bringen ist
A = −GM m
Z
r1
r0
µ
¶
1
dr
1
= −GM m
−
.
r2
r0 r1
Die erforderliche Arbeit, um einen Körper unendlich weit wegzubringen, ist daher
1
A = −GM m .
r0
Das Gravitationspotential
Die Arbeit pro Masse, die aufgewendet werden muss, um einen Körper ins
Unendliche zu befördern, wird Potential U genannt.
U = −GM/r
Dass der Nullpunkt im Unendlichen liegt, ist Konvention. Die Gravitationskraft
kann als “Steigung” des Potentials gedeutet werden:
~ d~r,
F~ d~r = −dU = −∇U
~ der sogenannte Gradient,
wo der Differentialoperator ∇,
∂U
∂U
∂U
~
~
~
~
+ êy
+ êz
.
∇ = êx
∂x
∂y
∂z
Damit
~
F~ = −∇U.
Fluchtgeschwindigkeiten
Als Anwendung des Potentialbegriffs untersuchen wir die Mindestgeschwindigkeit,
die eine Rakete haben muss, um die Erde zu verlassen.
An der Erdoberfläche muss gelten mg =
die erforderliche Arbeit gerade
GM m
2 ,
rE
2
also g = GM/rE
, und folglich ist
A = −mgrE.
Vorerst berechnen wir die Geschwindigkeit, mit der eine stabile Kreisbahn
möglich ist. Dazu muss die Zentrifugalkraft auf das kreisförmig bewegte (also
beschleunigte) Raumschiff gerade die Gravitationskraft kompensieren, also
mv 2 GM m
=
2
rE
rE
und damit
r
GM
rE
für ein “Raumschiff”, welches haarscharf über der Erdoberfläche um die
Erde saust. Bei tangentialem Abschuss reicht diese Geschwindigkeit, bei
Vernachlässigung der Reibung, gerade aus, damit die Rakete nicht auf den
Erdboden zurückfällt. Sie heißt oft “erste kritische Geschwindigkeit”.
v=
Die soeben beschriebene Rakete bleibt auf immer im Schwerefeld der Erde
gefangen. Die Geschwindigkeit am Erdboden einer Rakete, die das Schwerefeld der Erde verlassen soll, die “zweite kritische Geschwindigkeit” oder
“Fluchtgeschwindigkeit”, errechnet sich einfach mit 12 mv 2 =
v=
r
GM m
rE
= mgrE, also
2GME p
= 2grE ≈ 11.2 km/s.
rE
Diese Geschwindigkeit ist also notwendig, um von der Erde aus ins Unendliche zu
geraten. Oder reicht das etwa nicht?
v=
s
GM¯
= 42.1 km/s,
r¯−E
die “dritte kritische Geschwindigkeit” ist die Geschwindigkeit, die eine Rakete bei
der Erde braucht, um das Sonnensystem zu verlassen.
Wie fliegt ein Körper, der die Erde bzw. das Sonnensystem verlässt?
Das Potential innerhalb einer Hohlkugel
P
P0
Durch die gestrichelte Kugelfläche müssen
gleich viele Feldlinien hinein- wie hinauslaufen.
Auf jeden Punkt P muss, wegen der Kugelsymmetrie, dieselbe Kraft wirken.
Dies ist nur erfüllt, wenn gar keine Feldlinien
durch die Kugeloberfläche stoßen, also auf
P und P 0 keine Kraft wirkt.
Im Innern einer Hohlkugel wirken keine Kräfte, d. h. das Potential
ist konstant.
Das Potential außerhalb einer Kugel
dM = 2π y ρ ds da = 2π a ρ dx da
weil y = a sin θ . Also M = 4π a2 ρ da.
da
x
r
a
y
θ
O
m
R = OP P
dx
−a
a
r 2 = y 2 + (R − x)2 = y 2 + x2 + R2 − 2Rx
also r 2 = a2 + R2 − 2Rx und r dr = −Rdx
r = R + a für x = −a und r = R − a für x = −a
ds = dx/ sin θ dE = − G
P
m dM
r
Ra
EP = −2πρ G m a da −a drx
R R−a
EP = G 2πρ aRda m R+a dr = −G MRm
Das Potential einer Kugel ist dasselbe wie das eines Massenpunktes der Masse M .
Das Potential einer Kugel
r>a
r<a
U(r)
U(r) ~ -1/r
U(r) ~ r
2
r=a
r
Bewegung von zwei Körpern
Nun ist also das Gravitationsgesetz bekannt und die erforderliche Konstante G
gemessen. Man kann den Spieß jetzt umdrehen und z. B. die Planetenbahnen aus
dem Gravitations- und Impulserhaltungsgesetz herleiten.
Unterschied: Wir erkennen, dass die Bewegung um den gemeinsamen Schwerpunkt
verläuft! Bahnen können auch Hyperbeln oder Parabeln sein!
Allgemein: Bahnen sind Kegelschnitte (Ellipsen, Parabeln, Hyperbeln)
Die Rotation von Galaxien
v
Um auf einer Kreisbahn zu bleiben, muss
mv 2
G mM
=
r gelten,
r2
also
q
v = const.
GM
GM
2
=
=⇒
v
=
v
r
r .
1
√
∼ r
Beobachtungen der Rotationskurve von
Galaxien zeigen aber v ≈ const.
r
Deshalb muss die Masse mit wachsendem
v2r
galaktozentrischen Abstand zunehmen wie M (r) ∝ G .
Die Gezeiten
Die Bewegung des Erde-Mond-Systems um den gemeinsamen (und in der
Erde steckenden) Schwerpunkt kann als kontinuierliche Verschiebung der Erde
aufgefasst werden.
RS
Bei der Bewegung um den Schwerpunkt verschieben
sich Punkte, sie drehen sich nicht. Dies führt zu einer
~Z , die immer gleich groß ist
Zentrifugalkraft F
und in dieselbe Richtung vom Mond durch den Erdmittelpunkt hindurch zeigt.
Die Gravitation zeigt aber immer zum Zentrum des
Mondes!
~Z = mΩ2 RS
F
~G = GME MM ~r
F
r
2
r
Die Gezeiten II
F~z
F~z
F~g
F~g
Erde
F~z
F~z
F~g
F~z
F~z
F~g
F~g
F~z
F~g
S
F~z F~g
~g
F
~
Fz
Mond
F~g
Im Erdmittelpunkt (und nur dort!) heben sich die Gravitationskraft F~G und die
Zentrifugalkraft F~Z gerade auf, also F~G = −F~Z .
Die Richtung und der Betrag der Zentrifugalkraft sind also bekannt( −F~G),
die/der der Gravitationskraft in jedem Punkt auch. Im dem Mond abgewandtesten
Punkt lautet die Differenz der Kräfte auf einen Massenpunkt der Masse m
¶
µ
~r
1
mMM
−
1
∆F~ = −G 2
r
(1 + R/r)2
r
2mMM R~r
r3
r
R
= 2F~G(r) ,
r
≈ G
wo r der Abstand von Mond- zu Erdmittelpunkt ist, und R der Erdradius
bedeutet. Die Beschleunigung in dem Punkt ist sehr klein,
a=
m
∆F
= 1.1 · 10−6 2 .
m
s
Abstand Erde-Mond
3
lunar semimajor axis [10 km]
400
350
?
300
ocean model
present tidal
dissipation rate
250
−2000
−1500
−1000
6
time [10 y]
−500
(nach Bills und Ray, (1999))
0
Die schnelle Erdrotation führt über
die Reibung zu einer leichten Beschleunigung der Flutwellen gegenüber
der Mondlage. Diese eilen dem Mond also
leicht voraus, was zu einem Drehmoment
auf die Erde führt, welches ihren Drehimpuls verringert. Im System Erde-Mond
muss er aber erhalten bleiben, weshalb
der Mond ihn übernimmt (über die
leichte Gravitationskraft der Flutwelle!).
Verbesserte Formulierung des Gravitationgesetzes
Der Schwerpunkt Erde-Sonne oder Erde-Mond bleibt kräftefrei, d. h. dass sich die
Bewegung der Erde und Sonne unterteilen lässt in Bewegung des Schwerpunktes
und eine überlagerte Bewegung der Planeten.
GµM ~r
d2~r
µ 2 =− 2
dt
r r
Die Bewegung ist gleich der Bewegung eines Satelliten der reduzierten Masse
µ = m1m2/(m1 +m2) um die im Schwerpunkt festgehaltene Masse M = m1 +m2.
Beide Körper bewegen sich auf Ellipsen, in deren einem Brennpunkt der
Schwerpunkt sitzt.
Planetenbahnen
Zur Berechnung nutzen wir aus, dass die totale Energie sowie der Drehimpuls
erhalten sein müssen.
Etot = Ekin + Epot = const.
m 2 m 2 2
ṙ + r φ̇ + Epot
=
2
2
m 2
L2
ṙ +
Etot =
+ Epot denn
2
2
2mr
L = mr 2φ̇.
Also verändert sich die Geschwindigkeit
dr
=
dt
s
L2
µ
2
E − Epot −
m
2mr2
¶
und die Winkelgeschwindigkeit
L
dφ
=
denn
2
dt
mr
Division ergibt
dφ
=
dr
L = mr 2φ̇.
L
mr2
r ³
2
m
2
L
E − Epot − 2mr
2
´.
Mittels Integration erhält man nun eine Polardarstellung der Planetenbahn
r = r(φ).
Z
φ
φ0
L
dφ = φ − φ0 =
m
Z
dr
r2
r ³
2
m
L2
E − Epot − 2mr2
´
Mit φ0 = 0 und Epot = −GM m/r wird das Integral lösbar (nachschlagbar. . . )
φ = arccos
was mit den Abkürzungen
GmM
a=−
2E
Ã
L2/r − Gm2M
p
(Gm2M )2
und
²=
+
r
2mEL2
!
,
2EL2
1+ 2 3 2
G m M
einfacher aussieht
µ
2
¶
a(1 − ² ) − r
.
²r
Auflösung nach 1/r liefert eine Gleichung für Kegelschnitte:
φ = arccos
1 1 + ² cos φ
=
.
2
r
a(1 − ² )
Dies kann einfach gesehen werden: Obige Gleichung beschreibt z. B. eine Ellipse
mit großer Halbachse a und Exzentrizität ². Wir können in ein kartesisches
Koordinatensystem mit Ursprung im Brennpunkt S umrechnen, indem wir
schreiben ξ = r cos φ und η = r sin φ
a(1 − ²2) = r(1 + ² cos φ)
p
2
ξ 2 + η 2.
a(1 − ² ) − ξ² =
Eine Translation des Ursprungs in den Mittelpunkt der Ellipse (des Kegelschnittes)
erreichen wir mit der Transformation ξ = x+a² und η = y, womit nach Quadrieren
obiger Gleichung und Sammlung aller Terme mit ξ auf der linken Seite
ξ 2 + 2a²ξ − 2a²3ξ − ²2ξ 2 = −y 2 + a2(1 − ²2)2
ξ 2 + 2a²ξ + a2²2 − a2²2 − ²2(ξ 2 + 2a²ξ + a2²2 − a2²2) = −y 2 + a2(1 − ²2)2
(ξ + a²)2 − ²2(ξ + a²)2 − a2²2(1 − ²2) = −y 2 + a2(1 − ²2)2
(ξ + a²)2(1 − ²2) + y 2 = a2(1 − ²2)2 + a2²2(1 − ²2)
x2 y 2
y2
x2
= 2+ 2
+ 2
2
2
a
a (1 − ² ) a
b
= 1.
Kegelschnitte
²=1
r
b
a
2
φ
a²
²>1
a(1−² )
r = 1+
² cos φ
0<²<1
Kreis für ² = 0
Parabel für ² = 1
v0
0<²<1
2
r
b
φ
a
a(² −1)
r = 1+
² cos φ
²>1
v02 =
²=0
(1+²)GM
r
Mars Express
Aus den Anfangsbedingungen folgt
²=
Hohmann Transferorbit
v1
vM
rM
rE
v0
vE
rE v02
GM
−1
Für rE und rM die Ellipsengleichung
anwenden und dividieren führt zu
rM
²
= 11+
r
−²
E
Obiges Resultat für ² einsetzen ergibt
2rM /re
v02 = GM
r 1+r /r
E
M
E
Drehimpulserhaltung
besagt rE v0 = rM v1 und damit
2
rM v12
rE rE v E
2
GM = r
GM = 1+r /re < 1
M
M
Damit kann nun einfach ausgerechnet werden, um wieviel Mars Express bei der
Erde und bei Mars beschleunigt werden muss. Bei der Erde muss die Trägerrakete
also eine Geschwindigkeit v0 erreichen, die um ∆v0 = v0 − ve größer ist als ve.
Bei Mars muss der “Bus” die Sonde auf die Umlaufgeschwindigkeit beschleunigen
um ∆v1 = v1 − vm.
∆v0 = v0 − ve
∆v1 = v1 − vm
r
s
GM 
re

2rm/re 
=
1 − rm/re
s
Ã
!
r
GM
2
=
1−
rm
1 + rm/re
und die total notwendige Geschwindigkeitsänderung ∆vtot = ∆v0 + ∆v1.
Der Virialsatz
P
P
P
2K =
riṗi (∗)
pivi = ddt ( piri) −
Rτ
Mittelwertbildung < f >= limτ →∞ 0 dtf (t).
Ist F (t) beschränkt, so gilt < f >= 0, wenn f = Ḟ , denn
Rτ
< f >= limτ →∞ τ1 0 dt ddFt = 0.
Bei Mittelung fällt deshalb der erste Term in Glg.(∗) weg.
P ∂U
∂U
< 2K >=<
ri ∂r > weil ṗi = ∂r
.
i
i
Mit U ∼ 1/r finden wir
2 < K >= − < U > Virialsatz
Jeans-Kollaps und die Entstehung des Sonnensystems
Für eine kugelförmige, homogene interstellare Molekularwolke lässt sich die
potentielle Energie einfach berechnen. Die mittlere Dichte
M
ρ =< ρ >= 4π 3
3 R
und damit
4π 3
r <ρ>.
M (r) ≈
3
Die potentielle Energie eines Massenelementes dm = 4πr 2ρdr in einer Kugelschale
beträgt
M (r)r 2
dr
dU = −G4πρ
r
also
U = −4πGρ
Z
R
drM (r)r.
0
Integration ergibt
U
4π
= − 4πρ2G
3
Z
R
drr4
0
16π 2G 2 5
3 GM 2
ρ R =−
und nach Virialsatz
<U > = −
15
5 R
3 GM 2
.
<K> =
10 R
Wir kennen aber die mittlere kinetische Energie in der Wolke!
3
< K >= N kT,
2
M
wo N =
.
µmH
Ist nun 2 < K > < < U >, so kollabiert die Wolke.
2
3 GM
M
, woR =
kT <
3
µmH
5 R
¶1/3
µ
5kT
4π
ρ
< M 2/3 also
GµmH 3
¶1/2
µ
¶3/2 µ
5kT
4π
ρ
< M.
MJ =
GµmH
3
µ
4π M
3 ρ
¶1/3
Für M > MJ , die Jeans-Masse, ist die Wolke instabil, kollabiert, und bildet einen
Stern (evtl. mit Planetensystem).