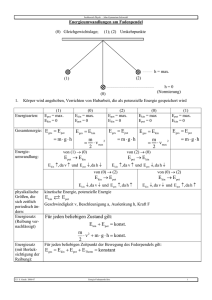
Gravitationsfeld

Physik Formelsammlung
Gravitationsfeld
1. Keplersches Gesetz
2. Keplersches Gesetz
3. Keplersches Gesetz
Alle Planeten laufen auf (kreisbahnähnlichen) Ein Planet bewegt sich geschwindigkeitsmäßig
Ellipsen um die Sonne um, deren Mittelpunkt so auf seiner Ellipse, dass der Fahrstrahl vom
all diesen Ellipsen als Brennpunkt gemeinsam Zentralkörper zum Planeten in gleich langen
ist. Der zweite Brennpunkt jeder Ellipse liegt Zeitspannen gleich große (aber von der Form
von Ellipse zu Ellipse anders und ist nur ein
her unterschiedliche) Teilflächen der Ellipse
math. Punkt im leeren Raum.
überstreicht.
Gravitationskraft
2
T1
2
2
T2
4
= 3 ==
=konst.
3
G⋅M
a1 a2
Gravitationsfeldstärke
1
F Grav=G⋅M⋅m⋅ 2
r
g  r =
mit Gravitationskonstante G:
3
4 2 T 2
11 m
G=
⋅ 3 =6,673⋅10
M a
kg⋅s 2
F Grav G⋅M
= 2
m
r
F Grav r =m⋅g  r 
Verschiebungsarbeit
im radialsymmetrischen Gravitationsfeld

W V  A  E =G⋅m⋅M⋅
1 1
ra r e

mit W V  A  E 0 für r A r E
Potentielle Energien im radialsymmetrischen Gravitationsfeld
Nullenergieniveau im Unendlichen
Nullenergieniveau auf Zentralkugeloberfläche (h=0)

1
E pot r =G⋅m⋅M⋅
r
E pot h=G⋅m⋅M⋅
mit E pot  r 0 und E pot ∞=0
1
1
R Rh

mit E pot h≥0
Potential
V  r =
E pot r 
1
=G⋅M⋅
m
r
V  r =

E pot r 
1
1
=G⋅M⋅ m
R Rh

W V  A  E =m⋅V  r E V r A =m⋅V
Für Potential im Punkt P bei zwei Zentralkörpern M 1 , M 2 :
V ges=V 1  M 1 P V 2  M 2 P
© VMH '04
Seite 1 / 2
http://VolkerMueller.Info
Physik Formelsammlung
Gravitationsfeld
Energieerhaltungssatz
gilt auf Kegelschnittbahnen, wenn sich der Körper mit Masse m antriebslos auf solch einer Bahn bewegt
E ges=E kinE pot =konst.
E kin 1 E pot 1=E kin 2E pot 2
Triebwerk an - Energieerhaltung vertan:
E ges nachher =E ges vorherW Triebwerk
Bei
E ges0
 Körper auf endlicher oder
geschlossener Bahn
E pot ∞=0 gilt:
E ges =0
 Körper kommt mit v ∞=0
ins Unendliche
E ges 0
 Körper kommt mit v ∞0
ins Unendliche
1. kosmische Geschwindigkeit
2. kosm. Geschwindigkeit = Fluchtgeschw.
Geschwindigkeit, die benötigt wird, um einen Körper auf eine
Umlaufbahn an der Oberfläche der Erde um die Erde zu bringen.
Geschwindigkeit, die in benötigt wird, damit ein Körper von der
Erdoberfläche weg ins Unendliche entkommt.
Ansatz:
Ansatz:
F Z =F Grav
E ges=0 bei E pot ∞=0
© VMH '04
Seite 2 / 2
http://VolkerMueller.Info