EE mgh = = ⋅ ⋅ EE mv 2 = = ⋅ EE mgh = = ⋅ ⋅ EE mv 2 = = ⋅ EE

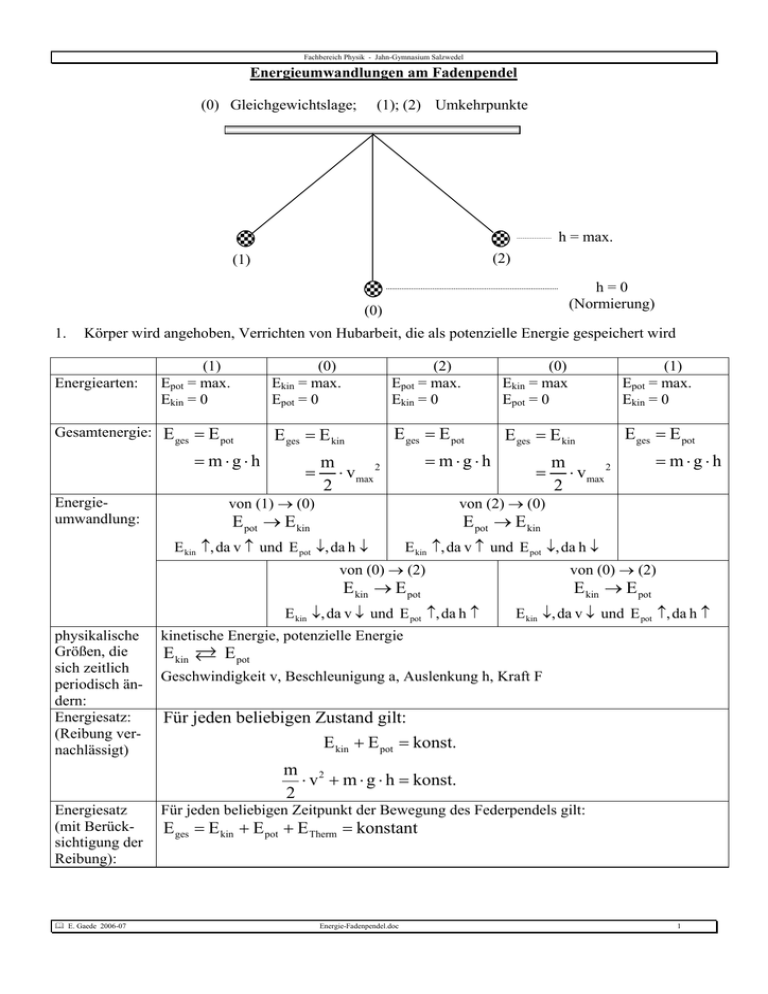
Fachbereich Physik - Jahn-Gymnasium Salzwedel
Energieumwandlungen am Fadenpendel
(0) Gleichgewichtslage;
(1); (2) Umkehrpunkte
h = max.
(2)
(1)
h=0
(Normierung)
(0)
1.
Körper wird angehoben, Verrichten von Hubarbeit, die als potenzielle Energie gespeichert wird
(1)
Epot = max.
Ekin = 0
(0)
Ekin = max.
Epot = 0
(2)
Epot = max.
Ekin = 0
(0)
Ekin = max
Epot = 0
(1)
Epot = max.
Ekin = 0
Gesamtenergie: E ges = E pot
E ges = E kin
E ges = E pot
E ges = E kin
E ges = E pot
Energiearten:
= m⋅g⋅h
Energieumwandlung:
=
= m⋅g⋅h
m
⋅ v max 2
2
=
von (1) → (0)
von (2) → (0)
E kin ↑, da v ↑ und E pot ↓, da h ↓
E kin ↑, da v ↑ und E pot ↓, da h ↓
E pot → E kin
= m⋅g⋅h
E pot → E kin
von (0) → (2)
von (0) → (2)
E kin ↓, da v ↓ und E pot ↑, da h ↑
E kin ↓, da v ↓ und E pot ↑, da h ↑
E kin → E pot
physikalische
Größen, die
sich zeitlich
periodisch ändern:
Energiesatz:
(Reibung vernachlässigt)
m
⋅ v max 2
2
E kin → E pot
kinetische Energie, potenzielle Energie
E kin R E pot
Geschwindigkeit v, Beschleunigung a, Auslenkung h, Kraft F
Für jeden beliebigen Zustand gilt:
E kin + E pot = konst.
m 2
⋅ v + m ⋅ g ⋅ h = konst.
2
Energiesatz
(mit Berücksichtigung der
Reibung):
E. Gaede 2006-07
Für jeden beliebigen Zeitpunkt der Bewegung des Federpendels gilt:
E ges = E kin + E pot + E Therm = konstant
Energie-Fadenpendel.doc
1