LB Energie und Arbeit - minus-p

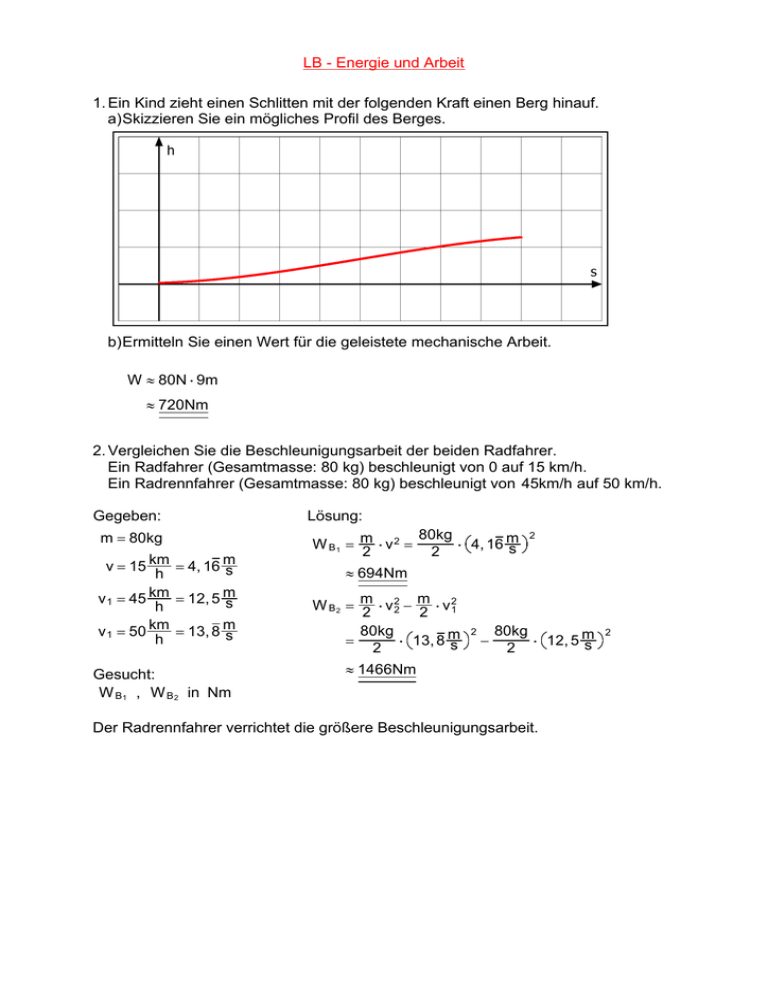
LB - Energie und Arbeit
1. Ein Kind zieht einen Schlitten mit der folgenden Kraft einen Berg hinauf.
a)Skizzieren Sie ein mögliches Profil des Berges.
b)Ermitteln Sie einen Wert für die geleistete mechanische Arbeit.
W l 80N $ 9m
l 720Nm
2. Vergleichen Sie die Beschleunigungsarbeit der beiden Radfahrer.
Ein Radfahrer (Gesamtmasse: 80 kg) beschleunigt von 0 auf 15 km/h.
Ein Radrennfahrer (Gesamtmasse: 80 kg) beschleunigt von 45km/h auf 50 km/h.
Gegeben:
m = 80kg
v = 15 km = 4, 16 m
s
h
v 1 = 45 km = 12, 5 m
s
h
v 1 = 50 km = 13, 8 m
s
h
Gesucht:
W B 1 , W B 2 in Nm
Lösung:
80kg
W B1 = m $ v 2 =
$ 4, 16 m
s
2
2
2
l 694Nm
W B 2 = m $ v 22 − m $ v 21
2
2
80kg
=
$ 13, 8 m
s
2
2
−
80kg
$ 12, 5 m
s
2
l 1466Nm
Der Radrennfahrer verrichtet die größere Beschleunigungsarbeit.
2
LB - Energie und Arbeit
3. In Kasan sprangen bei der Weltmeisterschaft im Klippenspringen vom 24. Juli bis
zum 9. August 2015 Frauen aus einer Höhe von 20 m und Männer aus
einer Höhe von 27 m hinunter ins Wasser.
a)Vergleichen Sie die potentielle Energie einer Frau (50 kg) und eines Mannes
(75 kg) beim Absprung.
Gegeben:
Lösung:
E pot 1 = m 1 $ g $ h 1
m 1 = 50kg
= 9810Nm
m 2 = 75kg
h 1 = 20m
E pot 2 = m 2 $ g $ h 2
h 2 = 27m
l 19900Nm
Gesucht:
E pot 1 , E pot 2 in Nm
b)Berechnen Sie für beide Sportler die maximale G eschwindigkeit beim Eintritt
ins Wasser. (Die Reibung kann vernachlässigt werden.)
Idee: Die potentielle Energie wird vollständig in kinetische umgewandelt.
E pot = E ∏kin
E pot = m v 2
2
v=
2 $ E pot
m
v=
2 $ E pot
m
2 $ 19900Nm
75kg
= 23, 0 m
s
v2 =
2 $ 9810Nm
50kg
l 19, 8 m
s
v1 =
4. Eine Volleyballerin schlägt den Ball mit einer Geschwindigkeit 72 km
h aus einer
Höhe h in das gegnerische Spielfeld. In diesem Spielfeld kommt der Ball mit einer
Geschwindigkeit von 75, 6 km
h auf dem Boden an.
Berechnen Sie die Höhe h.
(Hinweis: Die Reibung in der Luft soll vernachlässigt werden.)
Gegeben:
v 1 = 20 m
s
m
v 2 = 21 s
Gesucht:
h in m
Lösung:
E kin + E pot = E ∏kin
m v 2 + mgh = m v 2
2 1
2 2
1 v 2 + gh = 1 v 2
2 1
2 2
gh = 1 v 22 − 1 v 21
2
2
h=
Die Höhe beträgt etwa 2,10 m.
1 2
2 v2
− 12 v 21
g
h=
1
( m )2
2 21 s
h l 2, 1m
− 12 (20 ms )
9, 81 sm2
2
LB - Energie und Arbeit
5. Ein Körper mit der Masse m beschleunigt einen Wagen mit der Masse M.
a)Beschreiben Sie die Energieumwandlung des Systems.
Zunächst besitzt der Körper potentielle Energie.
Diese potentielle Energie wird stetig in kinetische Energie des Wagens und des
Körpers selbst umgewandelt. Es verbleibt also auch potentielle Energie beim
Körper, bis er den Boden erreicht.
b)Entwickeln Sie eine Formel zur Berechnung der Geschwindigkeit des Wagens.
E pot 1 = E pot 2 + E kin 1 + E kin 2
mgh 1 = mgh 2 + m v 2 + M v 2
2
2
mgh 1 = mgh 2 + m + M v 2
2
...
v=
2(mgh 1 − mgh 2 )
m+M