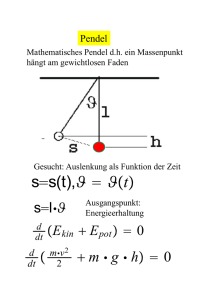
Die 10 Erhaltungsgrössen der klass. Mechanik

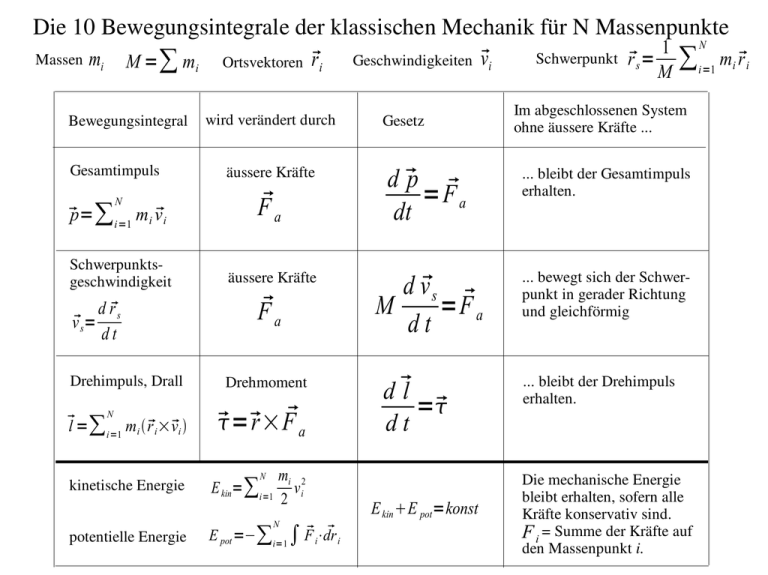
Die 10 Bewegungsintegrale der klassischen Mechanik für N Massenpunkte
Massen
mi
M =∑ m i
Bewegungsintegral
Gesamtimpuls
Ortsvektoren
ri
wird verändert durch
äussere Kräfte
p=∑i=1 mi vi
Fa
Schwerpunkts­
geschwindigkeit
äussere Kräfte
N
vs=
d rs
dt
Drehimpuls, Drall
N
l =∑ mi  ri ×
vi 
i=1
kinetische Energie
potentielle Energie
Fa
Drehmoment
= r × Fa
N
E kin=∑i=1
mi 2
v
2 i
N
i
E pot =−∑i=1 ∫ F i⋅dr
Geschwindigkeiten
vi
Gesetz
Schwerpunkt
1
rs =
M
∑i=1 mi ri
Im abgeschlossenen System ohne äussere Kräfte ...
d p 
=Fa
dt
... bleibt der Gesamtimpuls
erhalten.
d vs
M
= Fa
dt
... bewegt sich der Schwer­
punkt in gerader Richtung und gleichförmig
d l
=

dt
E kin E pot=konst
N
... bleibt der Drehimpuls
erhalten.
Die mechanische Energie bleibt erhalten, sofern alle
Kräfte konservativ sind.
= Summe der Kräfte auf F
i
den Massenpunkt i.