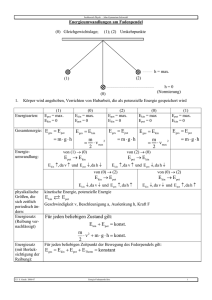
Z f Zusammenfassung Kapitel 2 Mechanik eines Massenpunktes
Werbung

Z Zusammenfassung f Kapitel 2 Mechanik eines Massenpunktes 1 Mechanik eines Massenpunktes idealisiertes Gebilde : alle Masse des Körpers p in einem Punkt konzentriert ► keine Berücksichtigung der Ausdehnung eines Körpers ► Ausdehnung d sei viel kleiner als die Dimensionen der Bahn (Länge, Radius) Ö Bewegung von Massenpunkten auf Bahnkurve im drei-dim. drei dim Raum Bahn = Variation der Koordinaten (x,y,z) (x y z) des Körpers mit der Zeit t O : Ort ⎛ x(t ) ⎞ ⎜ ⎟ r r (t ) = ⎜ y (t ) ⎟ ⎜ z (t ) ⎟ ⎝ ⎠ 2 Prinzipielles Vorgehen zur Analyse von Bewegungen eines Massepunktes : (1) Beschreibung B h ib der d Bahnkuve B h k : t3 z ⎛ x(t ) ⎞ ⎜ ⎟ r r (t ) = ⎜ y (t ) ⎟ ⎜ z (t ⎟ ( t ) ⎝ ⎠ y t1 (2) Berechnung der Ableitungen : ⎛ x& ((tt ) ⎞ ⎜ ⎟ r v (t ) = ⎜ y& (t ) ⎟ ⎜ z& (t ⎟ ( t ) ⎝ ⎠ t2 ⎛ &x&((tt ) ⎞ ⎜ ⎟ r a (t ) = ⎜ &y&(t ) ⎟ ⎜ &z&(t ⎟ ( t ) ⎝ ⎠ zo to x …oder oder umgekehrt umgekehrt, dd.h. h gegeben ist die Beschleunigung (bzw. (bzw Kraft) Berechnet werden durch Integration die Geschwindigkeit und die Bahnkurve 3 Beispiel (2) : gleichförmig beschleunigte Bewegung Gleichförmigg beschleunigt g Ö konstante Beschleunigung g g ⎛ ax ⎞ r& v ⎜ ⎟ & Ö Beschleunigung B hl i : r (t ) = a = ⎜ a y ⎟ = const. ⎜a ⎟ ⎝ z⎠ ⎛ a x t + v0, x ⎞ ⎟ v ⎜ r r Integration liefert v& v die Geschwindigkeit : v (t ) = r (t ) = ∫ a dt = ⎜ a y t + v0, y ⎟ = a t + v0 ⎜a t+ v ⎟ 0, z ⎠ ⎝ z Ö die Geschwindigkeit variiert linear in der Zeit; Anfangs-Geschwindigkeit v0 weitere Integration liefert die Bahn-Gleichung : ⎛ 1 2 a x t 2 + v0, x t + r0, x ⎞ ⎜ ⎟ 1v 2 r r r 2 1 r (t ) = ∫ v (t ) dt = ⎜ 2 a y t + v0, y t + r0, y ⎟ = a t + v0 t + r0 ⎜ 1 a t2 + v t + r ⎟ 2 0, z 0, z ⎠ ⎝ 2 z Ö der Ort variiert quadratisch in der Zeit; Anfangs-Ort r0 4 Gleichförmig beschleunigte Bewegung im Gravitationsfeld : Der freie Fall (a) Galileo Galilei ((1564-1642)) (a) Galileo Galilei entdeckte im 16. Jahrhundert, dass alle Objekte (unabhängig von der Masse !) mit derselben konstanten Beschleunigung fallen; die zurückgelegte Strecke ist proportional zum Quadrat der abgelaufenen Fallzeit; (b) Die regelmäßige (periodische) Mehrfach-Belichtung eines Fotos F d h das durch d Bild B ld eines fallenden f ll d Apfels A f l zeigt, dass d die zurückgelegte Strecke zwischen zwei Aufnahmen anwächst Ö die Bewegung des Apfels ist offensichtlich beschleunigt X Beispiele : freier Fall, waagerechter Wurf, schräger Wurf,… (b) 5 Kreisbewegung ► Winkelgeschwindigkeit g g ω macht Angabe g zur Geschwindigkeit g der Drehung g Ö Rotationsvektor Ö r ω = ω ωˆ mit dem Betrag ω (Winkelgeschwindigkeit) und der Richtung der Drehachse ω̂ r r r v =ω×r insbesondere gilt : r r v ⊥ω d.h. d h die Drehachse der Kreisbewegung ist senkrecht zur Geschwindigkeit r ω r v r r 6 Allgemeine („krummlinige“) Bewegung Ziel : allgemeiner g Ausdruck für Beschleunigung auf beliebiger Bahnkurve r r r v2 a = aT + a N = v& eˆT + eˆN ρ 7 Kräfte r r r& & F = ma = mr Ö Konsequenzen K : a=0 ⇒ F =0 d.h. ein freies Teilchen ändert seinen Bewegungszustand nicht und : Kraft ist Vektor, kann also aus Summe von Kräften resultieren r r Fges = ∑ Fi i Kraft und Impuls r r F = p& 8 Grundgleichungen der Mechanik : Newton‘sche Axiome JJeder d Körper Kö verharrt h i Zustand im Z d der d Ruhe R h oder der gleichförmigen geradlinigen Bewegung, g g, solange g keine Kraft auf ihn wirkt. 1. Newton‘sches Axiom r r Ö Der Impuls eines kräftefreien Teilchens p = mv ist zeitlich konstant Eine auf ein Teilchen wirkende Kraft führt r r zur Änderung seines Impulses & F=p 2 Newton‘sches 2. Axiom Einheit der Kraft : 1 kg·m/s2 = 1 Newton Zwei Körper, die miteinander wechselwirken, üben aufeinander gleich große, aber entgegengesetzt gerichtete Kräfte aus (actio = reactio) 3. Newton‘sches Axiom 9 Träge Masse & schwere Masse (Gewicht) Eigenschaft g eines Körpers p des Masse m ohne Krafteinwirkungg im Bewegungszustand zu verharren Ö „Trägheit“ Ö träge Masse mT Gewicht einer Masse durch F = mg (Gravitation) Ö schwere Masse mS In einem geschlossenen Fahrstuhl kann ein Experimentator grundsätzlich nicht entscheiden, ob der Fahrstuhl in einem homogenen Gravitationsfeld mit der Schwerebeschleunigung g ruht (Abb. a) oder ob er sich mit der Beschleunigung a=−g in einem gravitationsfreien Raum bewegt (Abb. b). Alle Experimente innerhalb des Fahrstuhls führen in beiden Fällen zu gleichen Resultaten. Resultaten 10 Kraftfelder ► wenn wir jjedem Punkt des Raums eindeutigg einen r r Kraft-Vektor zuordnen können, erhalten wir ein Kraftfeld F (r ) r r g tauchen in der Physik y Zentral-Kraftfelder auf : F (r ) = f ( r ) rˆ häufig Ö die Kraft zeigt immer auf ein festes Zentrum Ö Stärke der Kraft hängt (nur) von r ab. ab Ö f(r) < 0 : Kraft ist attraktiv (z.B. Gravitation) Ö f(r) > 0 : Kraft ist repulsiv (z.B. (z B zwischen gleichen elektrischen Ladungen) 11 Bewegung in Kraftfeldern : Potentielle & kinetische Energie F|| P F┴ Definition D fi i i der d Arbeit A b it längs lä eines i Weges von P1 nach P2 auf der Bahn: W12 = ∫ P2 P1 r r r F (r ) dr 12 Konservative/nicht-konservative Kraftfelder wenn die Arbeit in einem Kraftfeld unabhängig vom Weg ist, gilt : W= r r r ∫ F ( r ) dr = 0 P1 → P2 → P1 Ö das Kraftfeld heißt dann konservativ wenn die Arbeit in einem Kraftfeld abhängig vom Weg ist, gilt i.d.R. : W= r r r ∫ F ( r ) dr ≠ 0 P1 → P2 → P1 Ö das Kraftfeld heißt dann nicht nicht-konservativ konservativ 13 Potentielle Energie wie wir gesehen haben, hängt in einem konservativen Kraftfeld die Arbeit nur von den Koordinaten des Anfangs- und Endpunktes einer Bewegung ab; wir können daher die potentielle Energie eines Körpers im Punkt P definieren als die Arbeit, die zu leisten ist,, wenn man den Körper p von einem Bezugspunkt gp P0 nach P bringt g WP0 → P = ∫ P P0 r r r F (r ) dr ≡ E pot (P0 ) − E pot (P ) 14 Energiesatz der Mechanik Ö Ekin (P1 ) + E pot (P1 ) = Ekin (P2 ) + E pot (P2 ) Energieerhaltungssatz 15 Zusammenhang zwischen Kraft und Potential r ⎛ ∂E pot ∂E pot ∂E pot F = −⎜⎜ ; ; ∂y ∂z ⎝ ∂x r ⎞ ⎟⎟ = − ∇E ⎠ Kraft = Gradient d P des Potentials t ti l die Kraft zeigt in Richtung der größten (negativen) Variation des Potentials, d.h. in Richtung des Potential-Minimums 16 Drehimpuls Definition : r r r r r L = r × p = m (r × v ) verknüpft Ort mit Geschwindigkeit; beschreibt die Stärke der Dynamik bei der Bewegung auf einer Bahn 17 Drehimpuls und Drehmoment wir betrachten die zeitliche Veränderungg des Drehimpulses p : r& d (rr × pr ) r r L= = r ×F dt Ö Definition : r r& D=L r r r D = r ×F Ö Kraft mal Hebelarm Ö Drehmoment Ö die zeitliche Änderung des Drehimpulses ist gleich dem wirkenden Drehmoment vergleiche : die zeitliche Änderung des Impulses ist gleich der wirkenden Kraft 18 Präzession Drehimpuls ist Vektor Ö es ist möglich, dass Drehmoment D ≠ 0 die Richtung des Drehimpulses ändert (aber den Betrag u.U. konstant lässt) Ö Präzession r L r L ω ω z.B. Präzession eines Gyroskop-Kreisels : der Kreisel rotiert mit konstanter Winkelgeschwindigkeit; der Drehimpuls ist in Richtung der Drehachse ausgerichtet; bei der Präzession variiert die Richtung der Drehachse, d.h. die Richtung des Drehimpulses; L präzediert z.B. auf einer Kreisbahn; die Winkelgeschwindigkeit der Rotation (d.h. der Betrag des 19 Drehimpulses) wird u.U. nicht geändert bei der Präzession Gravitation und Planetenbewegung : Die Kepler‘schen Gesetze 1. Kepler 1 Kepler´sches sches Gesetz : Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht; physikalische Grundlage : EnergieErhaltung; Lösung der Bewegungsgleichungen im Gravitationspotential 2. Kepler´sches Gesetz : Der Radiusvektor von der Sonne zum Planeten überstreicht in gleichen Zeiten gleiche Flächen; physikalische Grundlage : D hi Drehimpuls-Erhaltung l E h lt i Zentralkraftfeld im Z t lk ftf ld J Kepler J. K l (1610) 3. Kepler´sches p Gesetz : Für das Verhältnis der Umlaufzeit T zur Länge a der grossen Halbachse der elliptischen Bahn gilt für alle Planeten: T2/a3 = const.; physikalische Grundlage : Lösung der Bewegungsgleichungen für 1/r-Potential 20 Effektives Potential für die Radial-Bewegung betrachte die Gesamt-Energie : Ö E = E pot + E rad kin +E E = E pot + Ekin = E pot 2 1 L + m r& 2 + 2 2mr 2 pot. Energie tan g kin kin Energie radial kin. kin. Energie g tangential g mit Drehimpuls verbundene Energie, die nicht für die Abstandsänderung dr/dt verfügbar ist Ö Definition des effektiven Potentials, in dem sich Radialbewegung vollzieht : ( eff ) tan g = E pot + Ekin = E pot E pot L2 + 2mr 2 beachte : Epot < 0 Ö attraktiv aber : L2/2mr2 > 0 Ö repulsiv tan g Zentrifugal-Potential Ekin 21