4. Arbeit und Energie

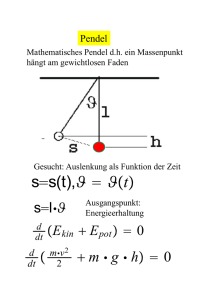
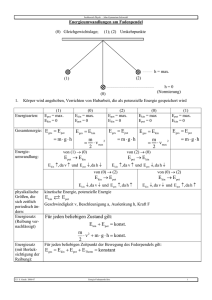
Mechanik – Arbeit und Energie
4.
Arbeit und Energie
4.1.
Mechanische Energie
−
Goldene Regel der Mechanik:
Was man an Kraft gewinnt, muss man an Weg zusetzen (und umgekehrt).
!
Offensichtlich ändert es das Ergebnis nicht, wenn sich Kraft und Weg ändern,
solange nur das Produkt aus Kraft und Weg konstant ist.
−
Definition: mechanische Arbeit
∆W = F ⋅ ∆ r
−
(1)
Arbeit ist ein Skalar
!
entscheidend ist die Kraftkomponente in Wegrichtung:
F ⋅ ∆ r = F ⋅ ∆ r ⋅ cos γ
= Ft ⋅ ∆ r
Ft ... Tangentialkomponente
Kräfte ⊥ Wegelement (Fn) leisten keine Arbeit (sog. Zwangskräfte)
−
Für einen makroskopischen Weg erhält man statt (1) verallgemeinert:
W=
∫ F ⋅ dr
(2)
Weg
−
Maßeinheit für die Arbeit ist das Joule: [W] = J
1 J = 1 Nm = 1 kg
m
s
2
SI
m
23
Mechanik – Arbeit und Energie
−
Beispiel: Beschleunigungsarbeit
F
dv
= m⋅
(2. NEWTONsches Axiom)
dt
Die Kraft ist der Trägheitskraft entgegengerichtet, die ihrerseits der Beschleunigung entgegengerichtet ist.
= ∫ F ⋅ dr
d r = v ⋅ dt
W
v2
dv
= ∫ m ⋅ v dt
dt
v
W
1
W
mit
m
m
= v 22 − v12 = ∆E kin
2
2
m 2
v
2
Ekin ... kinetische Energie, Bewegungsenergie
E kin ≡
(3)
Die beim Beschleunigen des Teilchens aufgewandte Arbeit steckt als Änderung
der kinetischen Energie in der bewegten Punktmasse.
−
Beispiel: Hubarbeit
= −m ⋅ g
F
(Minuszeichen, weil die aufzuwendende Kraft der Erdschwerkraft entgegengerichtet ist!)
r2
= ∫ − m ⋅ g ⋅ dr
W
r1
h
skalar:
W
= ∫ m ⋅ g ⋅ dr
0
(Bei skalarer Schreibweise fällt das Minuszeichen weg, weil dr und g entgegengerichtet sind.)
W = m ⋅ g ⋅ h = ∆E pot
∆Epot ... Änderung der potentiellen Energie (von 0 auf h)
(4)
24
Mechanik – Arbeit und Energie
4.2.
Potentielle Energie
−
gegeben: Kraftfeld lt. <3.2.>, also F = F( r )
−
Wenn man die Punktmasse quasistatisch mit der Kraft Fa gegen die Feldkraft F
verschiebt, wird die folgende Arbeit geleistet:
dW = Fa ⋅ d r = − F ⋅ d r
(5)
Integration ergibt für den Weg r1 → r2 :
r2
W ( r1 , r2 ) = − ∫ F d r
(6)
r1
−
Es zeigt sich, dass diese Arbeit für wichtige
Kraftfelder unabhängig vom Weg r1 → r2 ist:
!
Solche Kraftfelder heißen konservative Kraftfelder oder Potentialfelder.
Beispiele dafür sind die Gravitations- sowie die
elektrostatischen Felder.
Beide gehören zu den Zentralfeldern:
F = f (r ) ⋅
r
r
!
(7)
"
∃ nur Radialkomponente
F = f (r )
#
Alle Zentralfelder lt. Gl. (7) sind konservativ, und zwar im Prinzip mit beliebigem f(r). In der Realität existieren aber eben nur bestimmte.
−
Wegunabhängigkeit heißt also:
$
$
r2
r2
∫ F dr = ∫ F d r
%
%
%
%
$
r1
II
r2
'
r1
∫ F dr + ∫ F dr = ∫ F dr = 0
&
'
&
⇒
r1
I
'
−
(8)
$
r1
I
&
&
&
&
(9)
r2
II
'
Definition: potentielle Energie, Epot
dW = dE pot = −F ⋅ d r
(
(
(10)
25
Mechanik – Arbeit und Energie
bzw. in Integralform:
*
r2
W = − ∫ F d r = E pot ( r2 ) − E pot ( r1 )
)
)
)
)
(11)
*
r1
Vorzeichenwahl: Bewegung gegen die Feldkraft, d.h. F ⋅ d r < 0 führt zu ∆Epot > 0
bzw. W > 0.
Bemerkung: r1 und E pot ( r1 ) können dem Problem angepasst frei gewählt werden.
+
+
,
4.3.
−
-
Feldkraft und potentielle Energie
das totale Differential:
gegeben: Funktion z = f(x,y)
Es gilt:
dz = (dz )1 + (dz )2
∂z
∂z
⋅ dy
⋅ dx +
dz =
∂y
∂x
.
.
(partielle Ableitungen)
−
analog im 3D ist Epot = Epot(x,y,z):
⇒
−
dE pot =
∂E p
∂x
⋅ dx +
∂E p
∂y
⋅ dy +
∂E p
∂z
(12)
andererseits ist lt. Gl. (10):
dE pot = − Fx ⋅ dx − Fy ⋅ dy − Fz ⋅ dz
−
⋅ dz
(10‘)
Gleichsetzung von (10‘) und (12) liefert:
 ∂
∂
∂
F = − i
+j
+ k E p
∂y
∂z 
 ∂x
/
0
0
0
F = −grad E p = −∇ E p
1
(13)
mit ∇ ... Nabla-Operator
26
Mechanik – Arbeit und Energie
4.4.
−
Der Energiesatz der Mechanik
Multiplikation von Gl. (13) mit r = v :
3
3
2
2
F ⋅ r = −grad E pot ⋅ r
5
6
5
7
4
∂E pot   dx
∂E pot
 ∂E pot
dy
dz 
+j
+k 
+k
+j
= − i
 ⋅ i
∂z   dt
∂y
dt
dt 
 ∂x
d
= − E pot
dt
8
mit (12):
−
8
8
8
8
8
(14)
andererseits ist nach dem 2. NEWTONschen Axiom:
|⋅ r
= mr
=
;
F
9
:
<
:
F ⋅ r = mr ⋅ r
(3 - 2)
?
?
A
>
−
(15)
A
@
@
@
Es lässt sich leicht zeigen, dass:
d m 
d
E kin =  r 2 
dt
dt  2 
1
= ⋅ m ⋅ 2 ⋅ r ⋅ r = mr ⋅ r
2
C
B
E
E
D
−
D
E
D
E
D
D
D
Der Vergleich von (14), (15) und (16) liefert:
−
d
d
E pot = E kin
dt
dt
bzw.
d
d
E pot + E kin = 0
dt
dt
Die mechanische Energie (= Summe aus Ekin und Epot) ist in einem konservativen Kraftfeld (Potentialfeld) konstant.
−
(16)
(17)
!
Zur Rolle der Reibung:
Reibung verwandelt Ekin in Wärme (= ungeordnete Teilchenbewegung)
⇒ Verletzung des Energieerhaltungssatzes der Mechanik
!
(Wenn man die Wärmeenergie mit einbezieht, bleibt die Energie natürlich wieder erhalten.)
Reibung stört nicht die Impulserhaltung.
!
27