Vorlesung 4

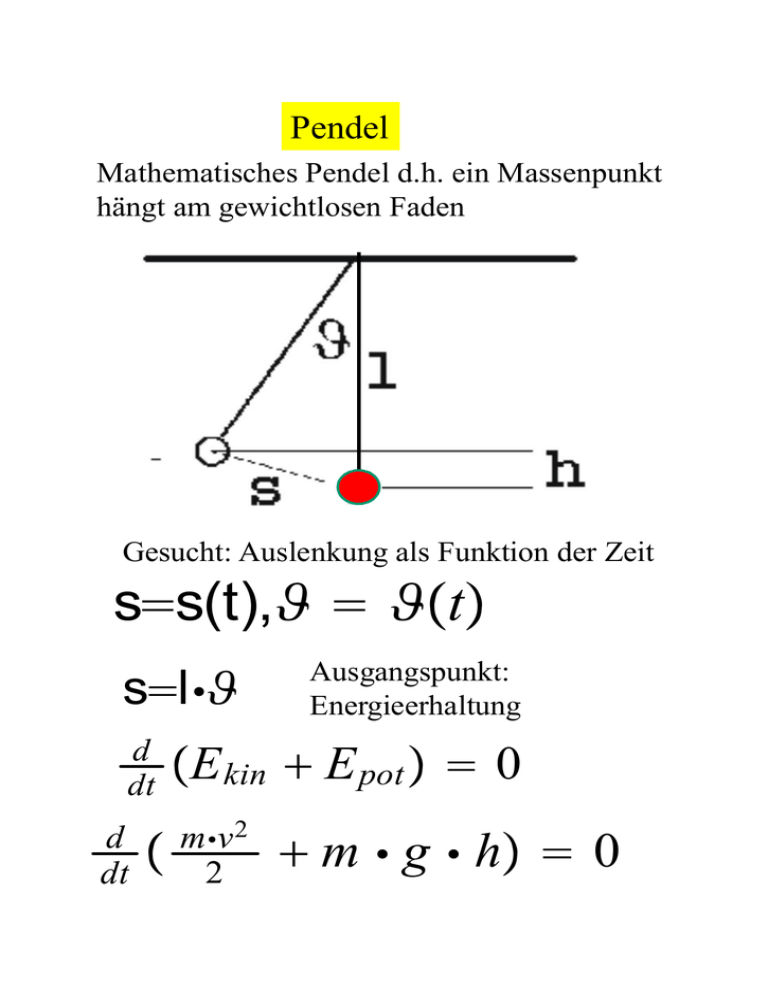
Pendel
Mathematisches Pendel d.h. ein Massenpunkt
hängt am gewichtlosen Faden
Gesucht: Auslenkung als Funktion der Zeit
s=s(t),h = hÝtÞ
s=l6h
d
dt
d
dt
Ý
Ausgangspunkt:
Energieerhaltung
ÝE kin + E pot Þ = 0
m6v 2
2
+ m 6 g 6 hÞ = 0
d
dt
Ý
m6l 2 6h 2
2
+ m 6 g 6 l 6 Ý1 ? coshÞÞ = 0
Näherungslösung, beschränkt auf kleine Winkel:
Da
cosh = 1 ?
1
2!
h2 +
1
4!
h 4 ?. .
1
bis h 4
0.75
0.5
cosh
0.25
bis h 2
0
0
0.25
0.5
0.75
1
1.25
Winkel (rad)
Mit
d
dt
E pot =
1
62
2
6 m 6 g 6 l 6 h2
Ý 12 6 m 6 l 2 6ÝhÞ + 12 6 m 6 g 6 l 6 h 2 Þ = 0
6
66
6
m 6 l 2 6h 6 h +m 6 g 6 h 6h = 0
66
Die Bewegungsgleichung h
+
m6g
l
=0
ist identisch mit der Gleichung, die mit einer Masse
an einer Feder erhalten wurde, wenn
D=
m6g
l
ist.
Mit der Schwingungsdauer T:
T = 2^
Bisher Kinematik, ausgedrückt in
l
g
und Dynamik mit
E pot = X F 6 ds
E kin =
m6v 2
2
1.6 Impuls
Kraft =m 6
=
dv
dt
m6Ý v ? v 0 Þ
At
oder in
=
At
m6 v ?m6 v 0
At
Neue Bewegungsgröße Impuls
Kraft=
Änderung des Impulses
Zeiteinheit
Kraft6Zeit=Änderung des Impulses
oder
F 6 At = m 6 v ? m 6 v 0
„Stoß“
Kraft wirkt kurzzeitig auf den Körper
der Masse m
F 6 At
Ändert Impuls aber
nicht notwendigerweise
die Energie
Kraft
Definition:
p = m6 v
ÝpÞ = kg 6 m 6 s ?1
Beispiel: Golfball (60g) erreicht 50m/s bei
einer Kontaktzeit von 5 6 10 ?3 s
Wie groß ist die Kraft?
F=
mv?mv0
At
=
0.06kg650ms ?1
5610 ?3 s
= 600kg 6 m 6 s ?2 = 600N
Im Erdfeld ist der Ball einer Kraft von mg=0.6N
ausgesetzt.
Zusammenhang zwischen
F =
dp
dt
p und E kin
auch in relativistischer Kinematik gültig
Aus dem dritten Newtonschen Axiom:
Actio=Reactio
F 12 = F 21
Verallgemeinerung auf beliebig viele
Massenpunkte
Gesamtimpuls des Systems:
In einem abgeschlossenen System
(keine Kräfte von außen) bleibt der
Gesamtimpuls erhalten
Definition des Schwerpunkts S
> i mi 6 r i
Verallgemeinerung: r S =
> i mi
Ým 1 + m 2 Þ 6 r S = m 1 6 r 1 + m 2 6 r 2
6
6
6
p = p 1 + p 2 Aus Impulserhaltung:
6
6
p=0
p = Konstante
66
Ým 1 + m 2 Þ 6 r S = a S = 0
Erhaltung des Schwerpunkts
eines Systems bestehend aus zwei oder
mehreren Massenepunkten
Wichtige Folgerung des Impulssatzes
Dies gilt unabhängig von Bewegungen und
Wechselwirkungen der Teilchen untereinander
Beispiel: Feuerwerkskörper
1.7 Weitere Anwendungen des Energieund Impulssatzes
Rückstoßantrieb
Eine Rakete mit der Masse m, stößt eine Treibstoffmasse dm in der Zeit dt mit der Geschwindigkeit w
aus.
Frage: Wie groß ist die Geschwindigkeit nach
einer Brenndauer t
Startwerte: t = 0, m = m 0 , v = 0
?w 6 dm = m 6 dv
mÝtÞ dm
Integration: X m 0 m = ln mÝtÞ ? ln m 0 =
?
1
w
vÝtÞ
X 0 dv = ? w1 6 vÝtÞ
Ann.: ? dm
= konstant = ?W ¸
dt
vÝtÞ = w 6 ln
m0
m 0 ?W6t
= ?w 6 lnÝ1 ?
W6t
m0
Þ
Raketenmasse besteht aus:
m 0 =m NÝNutzlastÞ + m TÝreibstoffÞ
m T = W 6 t BÝrenndauerÞ
vÝtÞ = ?w 6 lnÝ1 ?
t6m T
m 0 6t B
Þ dabei t ² t B
Mit der Maximalgeschwindigkeit:
v max = ?w 6 lnÝ1 ?
mT
m0
Þ
Beispiel: Luftheuler
v max = ?140 6 lnÝ1 ?
v = ?140 6 lnÝ1 ?
1.5
2.5
Þ = 128. 28m/s
t61.5
2.565
Þ
125
100
75
50
25
0
0
1.25
2.5
3.75
5
Zeit t (s)
Rakete fliegt mit v max
weiter
Beispiel:
Raketen in Anwendug:
Praktikabel
Mehrstufenraketen
Brennstoffbehälter werden
abgesprengt
z.B.: Saturnrakete: