DOC - Hu-berlin.de

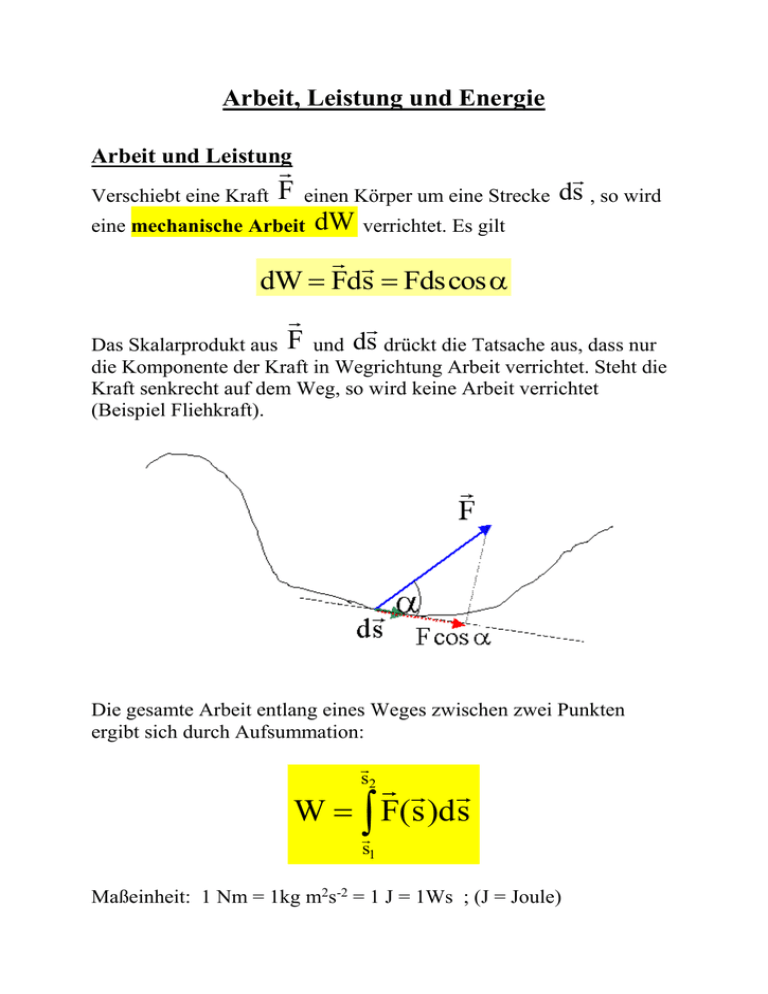
Arbeit, Leistung und Energie
Arbeit und Leistung
Verschiebt eine Kraft

F
einen Körper um eine Strecke

ds , so wird
dW verrichtet. Es gilt
 
dW  Fds  Fds cos 


F
d
Das Skalarprodukt aus
und s drückt die Tatsache aus, dass nur
eine mechanische Arbeit
die Komponente der Kraft in Wegrichtung Arbeit verrichtet. Steht die
Kraft senkrecht auf dem Weg, so wird keine Arbeit verrichtet
(Beispiel Fliehkraft).
Die gesamte Arbeit entlang eines Weges zwischen zwei Punkten
ergibt sich durch Aufsummation:

s2
  
W   F( s )d s

s1
Maßeinheit: 1 Nm = 1kg m2s-2 = 1 J = 1Ws ; (J = Joule)
In Komponentenschreibweise erhält man:
x2
y2
z2
x1
y1
z1
W   Fx dx   Fy dy   Fz dz
Leistung ist Arbeit, die je Zeiteinheit verrichtet wird:
 
dW Fd s
P

dt
dt
Ist die Kraft zeitunabhängig, so gilt

P  Fv
Die Leistung wird in J/s oder W (Watt) gemessen.
Arbeit und kinetische Energie
Aus dem zweiten Newton’schen Axiom folgt ein dynamisches
Kräftegleichgewicht zwischen der Summe der auf einen Körper der


F
F
Masse m wirkenden äußeren Kräfte A und der Trägheitskraft T .


FA  FT  0
Ersetzt man die Trägheitskraft durch den Newton’schen Ausdruck, so
folgt
 


FA ( r , t )  mr  0
Integriert man die Bewegungsgleichung nach dem Ort, so folgt


r
 

dv 
r FA ( r , t )dr  r m dt dr

0
0

r
Gehen wir auf der rechten Seite zur neuen Integrationsvariablen dv
über, so ist dies nur möglich, wenn auf der linken Seite der Gleichung
keine zeit- und geschwindigkeitsabhängigen Größen stehen. In diesem
Fall ist eine Trennung der Variablen (linke Seite: Integration über den
Ort; rechte Seite: Integration über die Geschwindigkeit) möglich.
Daher setzen wir im weiteren voraus, dass die Kraft nur vom Ort
abhängt. Dann gilt:


v
  
 
dv 
m 2 m 2
F
(
r
)
d
r


m
d
r


m
v
d
v


v  v0
r A
r dt
v



2
2
0
0
0

r'

r'
Die Größen auf der linken Seite der Gleichung heißen:

r'
Arbeit:
Kinetische Energie:
  
 FA ( r )d r

r0
m 2
v
2
Die an einem Teilchen/Körper verrichtete Gesamtarbeit
ist gleich der Änderung seiner kinetischen Energie.
Mechanische Energie


v2
  
 
dv 
m 2 m 2
F
(
r
)
d
r


m
d
r


m
v
d
v


v 2  v1
r A
r dt
v
2
2
1
1
1

r2

r2

r0

r2

r2
  
  
  
m 2 m 2




F
(
r
)
d
r

F
r
d
r

F
r
d
r


v 2  v1
r A
r A
r A

2
2
1
1
0
W  E pot,1  E pot, 2  E kin,1  E kin, 2
E  E kin,1  E pot,1  E kin, 2  E pot, 2
Der Begriff der mechanischen Energie bezeichnet die Energie der
mechanischen Bewegung Ekin und der mechanischen Energie der
Wechselwirkung von Körpern (Teilchen) Epot.
Für die kinetische Energie der Translationsbewegung gilt:
E kin 
m 2
v
2
Die potentielle Energie bezeichnet jenen Teil der mechanischen
Energie, der von der Lage der Körper (Teilchen) in einem äußeren
Kraftfeld abhängt. Sie ergibt sich aus der Arbeit, die dieses Kraftfeld
(Potentialkraft) verrichten muss, um die Körper von ihrem Ort

r0

ri
an
eine Position
im Kraftfeld zu verschieben, die definitionsgemäß
der potentiellen Energie Epot = 0 entspricht. Für einen einzelnen
Körper gilt dann:

r0
E pot


   F( x , y, z)d s

r
Der allgemeine Energiesatz sagt aus, dass die gesamte Energie beim
Verrichten von Arbeit erhalten bleibt. Dies bedeutet jedoch im
allgemeinen nicht, dass die mechanische Energie erhalten bleibt.
Wenn Arbeit verrichtet wird, so wird eine gewisse Energiemenge E
von einer Energieform in eine andere umgewandelt.
Man kann Leistung auch als einen Energiestrom auffassen, der der
Umwandlung von einer Energieform in die andere äquivalent ist.
Beispiele:
Arbeit gegen die elastische Kraft einer Feder
Das elastische Kraftfeld einer Feder wird durch das Hooke’sche
Gesetz definiert:


FH  D s
Eine äußere Kraft


FA   FH
verrichtet die Dehnungsarbeit W gegen die elastische Kraft von
s2
 
W   Dsds
s1
Greift die Kraft in der Richtung an, in welcher die Feder gestreckt
wird, erhalten wir im statischen Gleichgewicht:

D 2 2
W  s 2  s1
2

Die potentielle Energie einer Feder für die Dehnung s ergibt sich zu
0
E pot
 
s2
 D  s d s  D
2
s
wenn Epot = 0 für die Auslenkung s = 0 gesetzt wird.
Goldene Regel der Mechanik
Ist die Kraft längs eines Weges konstant, so gilt:

W  Fs
Falls die Arbeit gegeben ist, die man zwischen zwei Punkten s1 und s2
verrichten muss, so gilt:
W  const .  F1s1  F2s2
s1
und s 2 sind die Weglängen um vom Punkt 1 zum Punkt 2
zu gelangen. F1 und F2 sind die (hier als konstant vorausgesetzten)
Kraftkomponenten entlang der Wegrichtung. Es könnte sich um
verschiedene Wege handeln, auf einen Berg zu gelangen. Die übliche
Formulierung der Goldenen Regel lautet:
Was man an Kraft einspart, muss man an Weg zulegen.
Diese Regel wird bei der Konstruktion von mechanischen Maschinen
ausgenutzt. Einfachste Beispiele sind geneigte Ebene, Hebel,
Flaschenzug.