Drehimpuls und magnetisches Moment PDF

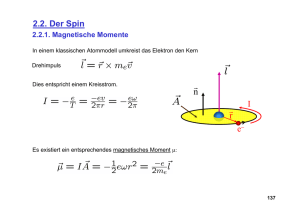
Drehimpuls und magnetisches Moment
Zusammenhang M
←→
l:
Z
1
Magnetisches (Dipol-)Moment: µ =
d3 r r×jLad , jLad = Ladungsstrom
2c
Strom für Q.M.-Teilchen: jLad = ejW ≡ ej , j = Wahrscheinlichkeitsstrom
1
[ψ ∗ p̂ψ + (p̂ψ)∗ ψ] , M = Teilchenmasse
j=
2M
Z
Z
¤
£
e
e
=⇒
µ =
d3 r r×[ψ ∗ p̂ψ + (p̂ψ)∗ ψ] =
d3 r ψ ∗ r× p̂ ψ + (r× p̂ ψ)∗ ψ
|{z}
|{z}
2M c
2M c
l̂
l̂
Z
Z
h
i
h
i
e
e
=
d3 r ψ ∗ l̂ψ + (l̂ψ)∗ ψ =
d3 r ψ ∗ l̂ψ + ψ ∗ l̂† ψ
2M c
2M c
=⇒
e
e
µ=
l=
Mc
Mc
Z
d3 r ψ ∗ l̂ψ
magn. Moment mit Drehimpuls verknüpft
“Quantisierung” des magnetischen Moments:
Wähle z-Achse = Polarisationsachse
ˆlz ≡ h̄m = −l, −l+1, ..., l
eh̄
=⇒ µz =
m
Mc
=⇒
Energieaufspaltung im Magnetfeld:
e
Hamiltonoperator im Magnetfeld Ĥ = −B · µ = −
B · l̂
2M c
eB ˆ
lz
wähle o.B.d.A. B = Bez =⇒ Ĥ = −B · µ = −
2M c
eh̄B
=⇒ Eigenwerte: Em = −
m , m = −l, −l+1, ..., l
2M c
=⇒ “Drehimpuls sichtbar gemacht”
Bohrsches Magneton µel =
=⇒
eV
h̄Hz
eh̄
= 0.58 ∗ 10−8
= 0.89 ∗ 107
2Mel c
Gs
Gs
Energiedifferenzen wesentlich kleiner als elektronische Übergänge
1
Messung des magnetischen Moments – Stern-Gerlach-Versuch:
Energie = E = −µ · B(r)
=⇒
Kraft = −∇E = ∇(µ · B(r))
inhomogenes
Magnetfeld
N
m=1
m=0
m=−1
Atomstrahl
Drehimpuls J
Anzahl M z: Ω = 2J+1
magnetische
Momente M z
∝ m=−J,...,+J
Messungen
Bsp. J=1
S
=⇒
1 !
= s ≡ “Spin”
2
Spin = “innerer Drehimpuls”
es gibt Atome mit Ω = 2 (!?)
Spin 6= Drehimpuls im Ortsraum
=⇒
2
=⇒
Aufspaltung µz ∝ m
sichtbar gemacht
Zahl der m-Werte = Ω
Ω ←→ Gesamt-Drehimpuls
=⇒
j=