Der Spin

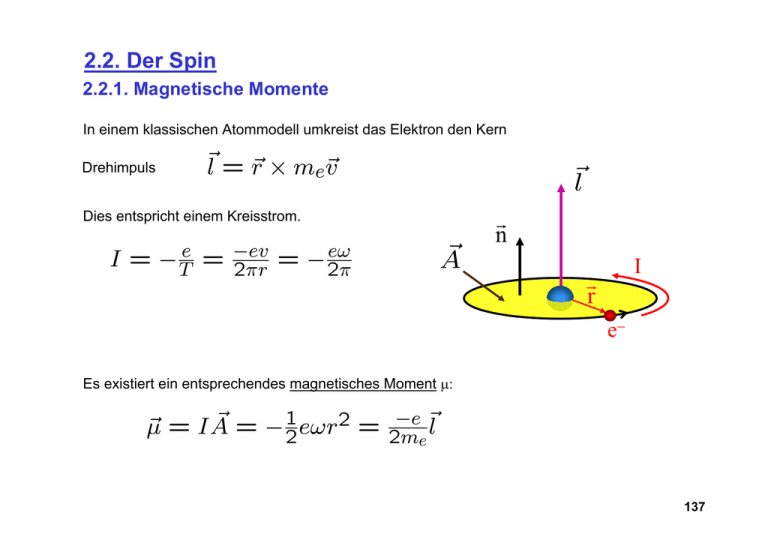
2.2. Der Spin
2.2.1. Magnetische Momente
In einem klassischen Atommodell umkreist das Elektron den Kern
Drehimpuls
Dies entspricht einem Kreisstrom.
r
n
I
r
r
e−
Es existiert ein entsprechendes magnetisches Moment μ:
137
Im Magnetfeld
hat der magnetische Dipol die potentielle magnetische Energie:
Das Feld übt ein Drehmoment
Präzession des Drehimpulsvektors
aus
z
r
B
Es ist
somit:
r
r
e−
I
Larmorfrequenz
138
In der Quantenmechanik ist der Drehimpulsoperator:
Nach dem Korrespondenzprinzip macht es Sinn, folgende Annahme zu machen:
mit
Bemerkung:
• Diese Annahme ist nicht trivial und erfordert eine Überprüfung.
•
•
ist ein „Einheitsmoment“ für ein klassisches Elektron auf einer Kreisbahn.
gibt die Abweichung vom klassischen zum quantenmechanischen Fall an, d.h. für
einen klassischen Bahndrehimpuls ist
!
139
heisst Bohrsches Magneton.
Analog kann man Einheitsmomente für andere Teilchen definieren, z.B. das Kernmagneton:
Die Konstante
heisst g-Faktor
für einen Bahndrehimpuls!
140
2.2.2. Stern-Gerlach Versuch
Die Quantisierung des Drehimpulses in z-Richtung kann im Stern-Gerlach-Versuch
direkt nachgewiesen werden.
Der Stern-Gerlach-Versuch nutzt man die Ablenkung im inhomogenen Magnetfeld.
Magnetisches Moment
parallel
Magnetisches Moment
antiparallel
Ablenkkraft im inhomogenen Magnetfeld auf Atome mit definierten Drehimpuls
da
von (2l+1) Linien.
:
erwartet man eine diskrete Schar
Klassisch: Kontinuum zwischen zwei Extremwerten!
141
Schematischer Aufbau des
Stern-Gerlach-Versuchs (1921)
B=0
Ag-Dichte
B>0
B>>0
0
z
Postkarte mit den Versuchsergebnissen
Gedenktafel Uni. Frankfurt
142
Zur Historie des Stern-Gerlach-Versuchs
Ag-Bedampfung auf der Detektorplatte
Gerlach
Stern
[Artikel in Physics Today, Dez. `03, von B. Friedrich, D. Herschbach]
143
Resultate des Stern-Gerlach-Versuchs:
• Beweis der Richtungsquantelung
• Messung der magnetischen Momente von Atomen
aber:
• Ablenkung von Atomen im s-Grundzustand mit l=0 (Experiment von Phillips und
Taylor 1927 mit neutralem Wasserstoff)
• Beobachtung einer geraden Anzahl von Linien
Postulat (Goudsmit und Uhlenbeck 1925):
Das Elektron besitzt einen inneren Drehimpuls, Spin, mit:
halbzahliger Drehimpuls
Hierzu gibt es kein klassisches Analogon!
144
Vektormodell des Spins:
Kugelradius
z
m S = + 12
y
r
s
m s = − 12
1
2
h
1
2
h
145
Aus dem Stern-Gerlach-Versuch folgt für das innere Moment des Elektrons:
somit
weitere Abweichung von der klassischen Erwartung
Der Spin erzeugt ein doppelt so grosses magnetisches Moment wie eine klassische
mit dem Drehimpuls
rotierende Kugel!
Der Spin folgt in logischer Weise aus einer relativistischen Beschreibung der Atome.
Formale Beschreibung Theorielehrbücher
Das sogenannte gyromagnetische Verhältnis
oder
kann auch direkt gemessen werden.
Versuch von Einstein und de Haas (1916)
146
Schema
Torsionspendel
+
−
z
Spiegel
vollständig
magnetisierter
Eisenzylinder
Historischer Aufbau (PTB)
Feldspule
Änderung aller N magnetischen Momente
Messung der Drehimpulsänderung im Torsionspendel
somit:
147
2.2.3. Die Feinstruktur des Wasserstoffspektrums
Eine genauere Betrachtung des Wasserstoffspektrums zeigt, dass die
Energieniveaustruktur nach der Formel
Spektrum der Balmer-Serie
nur näherungsweise gilt.
Hα-Linie
Wasserstofflampe
Beobachtung: Alle Energieniveaus
(mit Ausnahme der s-Zustände
spalten in 2 Niveaus auf. Man
beobachtet Dubletts.
Feinstrukturaufspaltung
148
Physikalische Erklärung der Feinstrukturaufspaltung:
Wechselwirkung von magnetischem Bahnmoment und Spin, Spin-Bahn-Kopplung
Erklärung der Dubletts:
• Spin parallel oder antiparallel zum Bahnmoment
• Bahnmoment = 0 für s-Zustände, d.h. keine Aufspaltung
Die Energieniveaus für die Feinstrukturaufspaltung können explizit berechnet werden.
Atomphysiklehrbücher
Feinstruktur der
WasserstoffEnergieniveaus
mit
Feinstrukturkonstante
Dabei ist j die Quantenzahl für den Gesamtdrehimpuls.
149
Feinstrukturaufspaltung
Größe der Aufspaltung
Bemerkungen:
• Die Energien hängen nur von n und j ab.
• Alle Energieniveaus werden abgesenkt.
• Niveaus (außer die mit s=0) spalten in Dubletts auf.
• Niveaus mit größerem j liegen energetisch höher.
• Die Aufspaltung hängt von der 4. Potenz der Kernladungszahl ab (nicht gezeigt), d.h.
sie liegt im Mikrowellenbereich beim Wasserstoff und bei ca. 6 Å bei den Na D-Linien.
150
Spektroskopische Notation
Multiplizität
Hauptquantenzahl
Bahndrehimpulsquantenzahl
N 2S+1LJ
Gesamtdrehimpulsquantenzahl
Spinquantenzahl
z.B. für Einelektronensysteme:
2 2S1/2
n=2, l=0, j=1/2
2 2P3/2
n=2, l=1, j=3/2
3 2P1/2
n=3, l=1, j=1/2
151
2.2.4. Die Hyperfeinstruktur und Lamb-Verschiebung
Die Hyperfeinstruktur
Auch das Proton (oder allgemeiner der Atomkern) besitzt (meist) einen Spin.
Wechselwirkung von Kernspin
mit dem Magnetfeld der Hüllenelektronen
(Spin und Bahndrehimpuls)
Hyperfeinwechselwirkung
Kernmagneton << Bohrmagneton
Hyperfeinaufspaltung << Feinaufspaltung
Magnetische potentielle Energie der Hyperfeinwechselwirkung:
magnetische Moment
des Protons
Wie bei der Feinstruktur fass man nun
und
mittleres Magnetfeld
der Hüllenelektronen
zum Drehimpuls
zusammen:
152
Es folgt
Atomphysiklehrbücher:
Hyperfeinstrukturaufspaltung
mit einer Konstante
Für Wasserstoff ist
oder
Somit:
Hyperfeinaufspaltung
153
Für Wasserstoff (n=1) ist die Aufspaltung:
entsprechend
oder
links: Hyperfeinstrukturaufspaltung
des Wasserstoffgrundzustandes
(21cm-Linie)
rechts: Messung der Verteilung von atomarem
Wasserstoff in unserem durch Spektroskopie
der 21-cm Linie (Messung der Entfernung
über Rotverschiebung)
154
Wasserstoff-Maser
1420 MHz als Übergang im Wasserstoffmaser (Frequenzstandard)
Erste Demonstration durch C. Townes 1953 in Columbia
Prinzip basiert auf stimulierter Emission von Mikrowellen in Resonanz mit dem
F=0
F=1 Übergang in atomarem Wasserstoff bei 1420 MHz.
155
Lamb-Verschiebung
Das Coulombgesetz ist eine Näherung für relativ große Distanzen. Bei sehr kleinen
Abständen der Ladungen treten Abweichungen auf, die sich aus der Quantisierung
es elektromagnetischen Feldes ergeben.
Quantenelektrodynamik (QED)
γ
e−
t
e−
virtuelles Photon, Energie ΔE
t+
Δt
e−
Schematische
Darstellung eines
QED-Prozesses
Verletzung der Energieerhaltung
Die Erzeugung virtueller Photonen wirkt sich als Zitterbewegung des Elektrons
aus.
Modifikation der Energieniveaus
156
Die Verschiebung der Energieniveaus ist umso größer, je kleiner der mittlere
Kernabstand der Elektronen.
V(r)
klassischer Bahnradius
0
Größte Modifikation für Zustände
mit j=1/2 !
r
V
Verschmierung durch
Zitterbewegung
Speziell Aufspalten der Energieniveaus
22S1/2 und 22P1/2
Experiment von Lamb und Retherford (1947)
Direkte Messung des Überganges
157
Das Experiment von Lamb und Retherford
metastabiles H (22S1/2 )
Willis Lamb Nobelpreis 1955
"for his discoveries concerning the
fine structure of the hydrogen spectrum"
158
Die ersten Energieniveaus von Wasserstoff für n=1 und n=2
45 μeV
4 μeV
10,3 eV
1,42 MHz
159
Vollständiges Spektrum des Wasserstoff
F=3,2
F=1,2
F=1,2
3D5/2
3D5/2
Achtung!
160