Document
Werbung

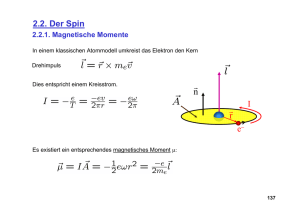
V10 : Elektronenspinresonanz Versuchsaufbau: Kontrollraum des Tandemgebäudes Betreuer SS 2008 - Robert Lahmann 09131/85-27147 , Raum TG223 [email protected] - Rezo Shanidze (Vertretung) 09131/85-27091 , Raum TG335 [email protected] Literatur : - S.A. Altschuler, B.M. Kosyrew: Paramagnetische Elektronenresonanz - A. Carrington, A.D. McLachlan: Introduction to Magnetic Resonance - F. Schneider, M. Plato: Elektronenpinresonanz - Ashcroft/Mermin: Solid State Physics - Haken, Wolf: Atom- und Quantenphysik Elektronenspinresonanz -- ESR ESR im Kontext der Atomphysik Energieniveaus in Atomen/Molekülen sind diskret Energieniveaus werden durch Photonen angeregt, bzw. Photonen werden ausgesendet beim “Abregen” eines Energieniveaus Energieniveaus sind i.d.R. entartet Aufgrund magnetischer Momente im Atom/Molekül wird diese Entartung durch äussere Magnetfelder aufgehoben. Dadurch entstehen neue Energieniveaus und neue Resonanzfrequenzen bei der Anregung Übergänge zwischen Energieniveaus werden durch Auswahlregeln beeinflusst (d.h. bestimmte Übergänge sind verboten) Je nach Übergängen und Art des Wechselwirkung zwischen Magnetfeld und magn. Moment des untersuchten Stoffes unterscheidet man: Zeeman-Effekt (normal, anormal) ESR Elektronenspinresonanz -- ESR Was ist ESR ? Die resonante Absorption von Mikrowellen durch eine Stoffprobe in einem Magnetfeld wird durch die ESR gemessen. Diese Absorption geschieht bei Proben die ein permanentes magnetisches Moment aufweisen (Paramagnetismus). Dieses magnetische Moment wird durch den Spin ungepaarter Elektronen erzeugt. Eine Substanz mit ungepaarten Elektronen ist z.B. Kupfersulfat. Kupfersulfat kommt als Pentahydrat vor: CuSO4 · 5 H2O wurde früher als Brechmittel benutzt, ist aber nicht ganz ungiftig ... Magnetische Momente r Klassisch betrachtet erzeugt ein Kreisstrom ein magnetisches Moment μ Man erwartet also in einem Atom (Molekül, r Ion) magnetische Momente: • des Bahndrehimpulses des Elektrons L , r • des Eigendrehimpulses r des Elektrons (Elektronenspin) S • und des Kernspins I Auf das magnetische Moment wirkt dann in einem Magnetfeld ein Drehmoment (→Präzession): und eine potentielle Energie von vgl. Kreisel: Präzessionsbewegung falls Drehachse nicht mit Richtung des Schwerkraftfeldes zusammenfällt → unterschiedliche Energieniveaus bei unterschiedlichen Vorzeichen r von μ ,z.B. bei spin up und spin down! Magnetisches Moment für Bahndrehimpuls Bei der Herleitung der magnetischen Momente kommt man mit klassischen Betrachtungen recht weit, aber nicht ganz bis ans Ziel; Berechnet man klassisch das magnetische Moment eines Elektrons auf einer Kreisbahn um den Atomkern (Wasserstoffatom) so erhält man Mit r μL = − r r r L = me ⋅ v × r μB r h (Bohrsches Magneton) ⋅L Bohrsches Magneton eh μB = = 9.2741 × 10 − 24 J/T 2m e Bahndrehimpuls Bahndrehimpuls des Elektrons auf der ersten Bahn des Bohrschen Wasserstoffatoms |Lr|= h Quantenmechanisch erhält man eine Quantelung des Drehimpulses || r L= l(l + 1 )h l = 0, 1, 2, . . . (Drehimpulsquantenzahl) Spin im Magnetfeld • Klassisch ist der Spin S die “Rotation” des Elektrons • Das magnetische Moment des Elektrons ist: r μS = −gS μB r h ⋅S g- (oder Lande-) Faktor: gs = 2 (Dirac) 2,0023 (QFT) • Im Magnetfeld kann der Spin sich in zwei Richtungen ausrichten Landé-Faktor und gyromagnetisches Verhältnis Der Landé-Faktor (oder g-Faktor) ist eine charakteristische Größe für atomare und nukleare Systeme (Meßgröße !) Bestimmt Proportionalität zwischen Drehimpuls und magnetischem Moment: r μL = −gL μB r h r ⋅L =γL ⋅L und r μS = −gS μB r h r ⋅S =γS ⋅S wird gyromagnetisches Verhältnis genannt. Experimentell: (reiner Bahnmagnetismus) (reiner Spinmagnetismus) Bahndrehimpuls +Spin im Magnetfeld • Im Allgemeinen hat ein Atom mehr als 1 ungepaartes Elektron • Für 2 Elektronen in “leichten Atomen” tritt die LS-Kopplung ein: r r r S = s1 + s2 r r r L = l1 + l2 r r r J = L+S S=0 , 1 , 2 L = l1 + l2 , l1 + l2 −1,K, l1 − l2 Definierte Grössen: r r r r r J , m J , L , m L , S , m S , li , s i (l1 ≥ l2 ) Auswahlregeln für optische Übergänge: ΔL = 0,±1 Δl = ±1 Landé-Faktor von Bahndrehimpuls und Spin und sind im Allgemeinen nicht parallel. Für den zeitlichen Mittelwert des mag. Momentes kann man mit dem Landé-Faktor gJ schreiben: Im Vektormodell erhält man: g J = g J (L, S, J ) = 1+ J ( J +1) − L (L +1)+ S (S +1) 2J ( J +1) (L=0, S=1) (L=1, S=0) Übergänge bei ESR Ein äusseres Magnetfeld B0 spaltet Zustände auf; Mikrowellen werden eingestrahlt um Übergänge (Absorption) mit Δms = ±1 anzuregen. Übergang ΔE (m = 1 / 2 → m = −1 / 2 ) = g ⋅ μ B ⋅ Bz Richtungsabhängigkeit des Landé-Faktors - 1 In Realität kein Isoliertes System: innere WW führen zu material- und richtungsabhängigem g (Anisotropie) mathematisch : Landé-Faktor als Tensor 2.Rangs Messung von g erlaubt Rückschlüsse auf Struktur des Festkörpers z.B. einkristallines CuSO4·5H2O 3 Diagonalelemente Richtungsabhängigkeit des Landé-Faktors - 2 Es gilt: falls die Drehachse, um die der Kristall während des Experiments gedreht wird, mit einer der -Achsen (Hauptachsen) zusammenfällt. Die Werte für die Landé-Faktoren in Achsenrichtung sind: Das ist die Messaufgabe des Versuches ! ESR -- Mikrowellen Mikrowellen: Wellenlänge: 1m Ö 1mm Frequenz : 300 Mhz bis 3 Ghz Energie : 10-6 eV Ö 10-5eV Radartechnik, Mikrowellenofen (2.455 Ghz), Mobilfunk (900 Mhz, 1.8-2.1 Ghz), WLan (2.4 Ghz, 5 Ghz) ESR -- Prinzip Prinzipielle Funktionsweise: Messung der Absorption von Mikrowellen durch eine Probe Absorption und Emission Absorption ΔE = E2 - E1 = hν Spontane Emission Stimulierte Emission (Kohärenz) Absorption bei ESR: Besetzung der Energieniveaus : Boltzmann-Statistik Versuchsaufbau - Übersicht IDiode Probe Probe Lock-inVerstärker Klystron Diode Klystron LockIn Frequenzmesser Cavity Resonator NFGen Netzgerät x1, x2, tSchreiber B0 Hohlleiter B-Feld I für B 0 x1 x2 U~B0 Strahlung liegt bei ESR im Mikrowellenbereich : Verwendung von entsprechender Hochfrequenztechnik wie Klystron, Hohlleiter etc. im Versuchsaufbau Klystron Aufgabe: Erzeugung von Mikrowellen Ein Elektronenstrom wird durch zeitlich veränderliche Gitterspannungen geschwindigkeitsmoduliert Nach einer gewissen Laufstrecke wird aus dieser Geschwindigkeitsmodulation ein dichtemodulierter Elektronenstrom Dieser dichtemodulierte Elektronenstrom erzeugt in einem Hohlraumresonator ein Feld aus welchem die Mikrowellen entstehen Hohlraumresonator Aufgabe: Verstärkung des Effekts der Spinresonanz Aufbau: geschlossener, meist quaderförmiger Metallkasten, in dessen Inneren elektromagnetische Schwingungsmoden mit bestimmten Eigenfrequenzen angeregt werden können; (Quantenmechanisch : Potentialtopf) Wichtig: - Wechsel der Probe ändert die Eigenfrequenz, da die Dielektrizitätskonstanten ε der Proben verschieden sind - Änderung der Probenausrichtung ändert ebenfalls die Eigenfrequenz => Im Versuch Abgleich der Klystronfrequenz nötig Lock-in-Verstärker Aufgabe: Verstärkung/Filterung des Ausgangssignals Das zu messende Signal ist sehr klein und muß geeignet verstärkt werden. Durch Modulierung des Signals mit einem Schaltsignal einstellbarer Frequenz werden Signale dieser Frequenz Verstärkt wohingegen andere Frequenzen des Signals rausgemittelt werden. Modulation Magnetfeld Absorptionskurve 1. Schritt: Feldmolulation Umsetzung Feldmodulation in Amplitudenmodulation Lock-in-Verstärker 2. Schritt: Herausfiltern des modulierten Signals durch Schaltfuntion: Vielen Dank für die Aufmerksamkeit und viel Spaß bei diesem Versuch!