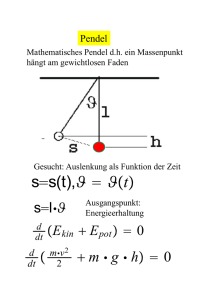
Herleitung der Formel für die kinetische Energie

Physik * Jahrgangsstufe 8 * Theoretische Herleitung der Formel E kin 
Fällt ein Gegenstand der Masse m in der Zeit t die Höhe h
herab, so verliert er dabei die Lageenergie Epot  m  g  h .
und damit t 
(*) mit g  9,8
v
(**)
Mittlere
Geschwindig-
Fallhöhe h
dafür
benötigte
Zeit t
m
.
s2
Die mittlere Geschwindigkeit v während der Fallzeit t
für die Fallhöhe h kann man aus h und t errechnen:
Startgeschwindigkeit 0
Startlinie
Gleichzeitig nimmt dabei die Geschwindigkeit v zu,
wobei wegen der konstanten Fallbeschleunigung g
gilt: v 
1
 m  v2
2
keit
v
Momentangeschwindigkeit v
nach der Zeit t
und der Fallhöhe h
Da die Geschwindigkeit während der Zeit t von der
Startgeschwindigkeit 0 auf die Momentangeschwindigkeit v
gleichmäßig zunimmt, gilt zwischen v und v der Zusammenhang
v
(***) .
Setze in die Gleichung (***) die beiden anderen Gleichungen (**) und (*) ein und zeige,
dass folgender Zusammenhang zwischen v, h und g besteht:
v
2g h
v
und damit
1 2
v  gh .
2
v
Beim Herabfallen um die Höhe h wird die Lageenergie Epot  m  g  h
in
kinetische Energie E kin umgewandelt, die zu der Geschwindigkeit v gehört.
Es gilt daher für die zur Geschwindigkeit v gehörende kinetische Energie:
1
E kin,bei der Geschwindigkeit v  E pot ,oben  m  g  h  m   v2
2
Insgesamt folgt also:
Bewegt sich ein Gegenstand der Masse m mit der Geschwindigkeit v,
so besitzt er die kinetische Energie
E kin 
1
 m  v2
2
Aufgaben:
1. Wie groß ist die kinetische Energie eines 100m-Sprinters (80 kg), der etwa 10 m/s läuft?
2. Ein Ball fällt von einem 75cm hohen Tisch herab.
Mit welcher Geschwindigkeit trifft er auf dem Boden auf?
Hinweis: Denke daran, dass die Lageenergie des Balls vollständig in kinetische Energie
umgewandelt wird.
Warum spielt die Masse des Balls dabei keine Rolle?
3. Aus welcher Höhe muss man einen Stein fallen lassen, damit dieser mit einer Geschwindigkeit
Von 100 km/h am Boden aufschlägt?
Physik * Jahrgangsstufe 8 * Theoretische Herleitung der Formel E kin 
Fällt ein Gegenstand der Masse m in der Zeit t die Höhe h
herab, so verliert er dabei die Lageenergie Epot  m  g  h .
Wegen der konstanten Fallbeschleunigung g gilt:
v  g  t und damit t 
v
m
(*) mit g  9,8 2 .
g
s
Für die mittlere Geschwindigkeit v während der Fallzeit t gilt:
v
h
t
(**)
Da die Geschwindigkeit während der Zeit t von der
Startgeschwindigkeit 0 auf die Momentangeschwindigkeit v
gleichmäßig zunimmt, gilt zwischen v und v der Zusammenhang
1
 m  v2
2
Startgeschwindigkeit 0
Startlinie
Mittlere
Geschwindig-
Fallhöhe h
dafür
benötigte
Zeit t
keit
v
Momentangeschwindigkeit v
nach der Zeit t
und der Fallhöhe h
v  2 v
(***) .
Aus den drei Gleichungen (***) , (**) und (*) folgt:
h
h 2g h
2g h
1
 2 
also v 
und damit v 2  2  g  h bzw. v 2  g  h
v
t
v
v
2
g
Beim Herabfallen um die Höhe h wird die Lageenergie Epot  m  g  h in
v  2 v  2
kinetische Energie E kin umgewandelt, die zu der Geschwindigkeit v gehört.
Es gilt daher für die zur Geschwindigkeit v gehörende kinetische Energie:
1
E kin,bei der Geschwindigkeit v  E pot ,oben  m  g  h  m   v2
2
Insgesamt folgt also: Bewegt sich ein Gegenstand der Masse m mit der Geschwindigkeit v,
so besitzt er die kinetische Energie
E kin 
1
 m  v2
2
Aufgaben:
1
1
kg  m2
 m
2
1. E kin   m  v   80kg  10   4000
 4, 0 kJ
2
2
s2
 s
2
1
1
 m  v2  g  h   v2  v2  2  g  h 
2
2
2
m
m
m
m
v2  2  9,8 2  0, 75m  v 2  14, 7 2  v  14, 7
 3,8
s
s
s
s
Der Ball trifft mit 3,8 m/s auf dem Boden auf.
Die Masse kürzt sich aus dem Ansatz zur Energieerhaltung heraus.
Alle Gegenstände fallen unabhängig von ihrer Masse mit der gleichen Beschleunigung herab.
2. E pot,oben  E kin,unten
 mgh 
3. E pot,oben  E kin,unten
 mgh 
1
1
 m  v2  g  h   v2  v2  2  g  h 
2
2
100 m 2
km 2
(
)
)
v
1002
m2 s2
3, 6s
h
h




  39 m
2
2
m
m
2g
3,
6

2

9,8
s
m
2  9,8 2
2  9,8 2
s
s
2
(100