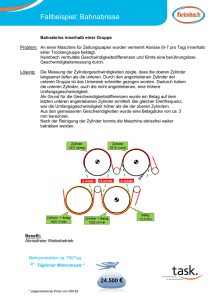
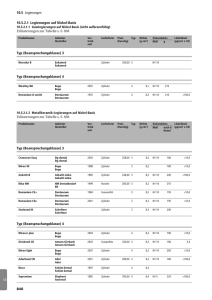
Somit erhält der Zylinder eine zusätzliche Beschleunigung

Der Magnuseffekt - Hörsaalversuch
 


 v 0 . Die
Ein Zylinder wird mit v 0 angeströmt und rotiert mit
Relativgeschwindigkeit der Gasströmung bezüglich des rotierenden
Zylinders ergibt sich dann folgendermaßen:
Oberseite:
 


v oben  v 0    r
Unterseite:

  
v unten  v 0    r
Die Anwendung der Bernoulligleichung liefert die Differenz der
statischen Drücke zwischen Unter- und Oberseite:
 2
 2
p oben  v oben  p unten  v unten
2
2
also die Druckdifferenz
p  p unten  poben 
 2
voben  v 2unten
2


Nach dem Ausrechnen erhält man für die Druckdifferenz:
 
p  2 r v0   
Damit ergibt sich die Kraft auf ein Oberflächenelement da zu


  
dFM  2r  v    dAeff
Die Gesamtkraft ergibt sich durch Integration über die gesamte
(halbe) Oberfläche.
Wir betrachten ein Oberflächenelement dA = hrd mit h als
Zylinderlänge. Also gilt:

   
dFM  2  hr  v    r d
Wir interessieren uns für die momentane Gesamtkraft, wenn die
momentane Geschwindigkeit v(t) gegeben ist. Das Skalarprodukt
innerhalb der eckigen Klammern ergibt:


 
dFM  2 hr  v   cos   r d
Das Kraftelement d wirkt somit in Richtung des Radiusvektors
(blau-azur). Da derselbe Vektor auf der unteren Zylinderhälfte
gespiegelt angreift, bleibt in der Summe nur die nach „rechts“
gerichtete Komponente (rot-pink) übrig. Für den Betrag von dFM
erhält man somit:
 
dFM  2 hr  v   cos  r cos d
Die Gesamtkraft folgt daher durch Integration zu

2 
FM  2  hr v  

2
 
 cos  d  hr v  
2

2
2
Die Magnuskraft lässt sich daher durch folgende Beziehung
ausdrücken

 
2
FM   hr  v   
mit h als Zylinderlänge. Hat der Zylinder die Masse m, so unterliegt er
der Querbeschleunigung

 
 hr 2  Luft  
v    Cv   
aM 
m Zylinder
Die Konstante C ist dimensionslos und hat in unserem
Hörsaalexperiment den Betrag C = 1,4.10-2. Sie hat eine anschauliche
Bedeutung:
 Luft
C
 Zylinder
bzw.
aM 
 Medium  
v   
 Körper
Die Größe C entspricht dem Verhältnis der Dichte des Fluids (hier
Luft) zur mittleren Dichte des rotierenden Körpers
Im folgenden Video ist der Flug des rotierenden Zylinders dargestellt.
Der Zylinder schlägt hörbar nach 3,4s auf. Infolge der Bewegung
entsteht eine Unschärfe, die den Zylinder als rechteckige Fläche
erscheinen lässt.
Nachdem der Zylinder mit dem Motor (Drehzahl 2000 U/min)
aufgezogen wurde, wird er mit einem kurzen Vorwärtsimpuls
abgelassen. Im Rechenbeispiel wird mit einer horizontalen
Anfangsgeschwindigkeit von 1m/s gerechnet. Im freien Fall würde er
nahezu senkrecht innerhalb einer Sekunde nach unten fallen.
Tatsächlich bewegt er sich auf einer schrägen, anfangs abgeflachten
Bahn mehrere Meter in den Raum hinein. Die gesamte Flugzeit betrug
3,4s. Kurz vor dem Erreichen der Hörsaalwand schlägt die Rolle in
7,1m Entfernung auf.
Aus den Einzelaufnahmen des Videos (30 Bilder je Sekunde) kann
folgende Trajektorie konstruiert werden:
Magnuseffekt - Trajektorie
7,000
6,000
5,000
z/m
4,000
3,000
2,000
1,000
0,000
0,000
1,000
2,000
3,000
4,000
5,000
6,000
7,000
8,000
x/m
Folgendes geschieht:
 Durch den nahezu freien Fall während der Anfangsphase des
Fluges gewinnt der Zylinder eine vertikale
Geschwindigkeitskomponente vz, die dem Zylinder durch den
Magnuseffekt eine horizontale Geschwindigkeitskomponente vx
(Vortrieb) verleiht.
 Die Horizontalbewegung schließlich führt zu einem
dynamischen Auftrieb, der den Zylinder wieder steigen lässt.
 Berücksichtigt man eine Abbremsung durch den Luftwiderstand,
so führt dies im Effekt zu einem geringeren Auftrieb. Der
Luftwiderstand bewirkt schließlich, dass sich der Zylinder
nahezu geradlinig gleichförmig bewegt.
Die Rechnung sieht folgendermaßen aus:
Die Gesamtbeschleunigung ages ergibt sich als Summe der
Erdbeschleunigung g und der Beschleunigung durch den
Magnuseffekt aM :

 
a ges  g  a M
Mit

 
a M  Cv   
bzw. unter Verwendung der Abkürzung


  C gilt:

 
aM  v  
Die Vektoren
Höhe):

v
und


haben folgende Komponenten (x-Weite, z-

v  v x ,0, v z 

  0, ,0
  2,9s 1
Der Betrag für Ω folgt aus dem Betrag für C und der Drehzahl des
Motors 2000 U/min.
Berechnet man das Kreuzprodukt, so erhält man schließlich:



a M   v z  i  v x k


Die Gesamtbeschleunigung erhält man mit g   gk (g = 9,81m/s²) zu



a ges   v z  i  v x   g k
Die Bewegung wird durch den Luftwiderstand gebremst. Die Kraft,
mit der der Zylinder gebremst wird, folgt aus der Gleichung



2 v
F  kv  kv v
v
Somit erhält der Zylinder eine zusätzliche Beschleunigung





k 
a Lw   v v  C W v v  C W v v x i  v z k
m

Die Größen CW und v ergeben sich zu
cw
CW 
A
2m
bzw.
v
v
2
x
 v 2z

Für unseren Zylinder im Hörsaalversuch erhält man mit cw  1 den
Betrag Cw  0,18 m-1 für die projizierte Zylinderfläche bzw. Cw 
0,56m-1 für die gesamte Zylinderfläche.
Die Gesamtbeschleunigung erhält man somit zu



a ges   v z   CW v v x i  v x   g  CW v v z  k
Da die zeitabhängige Geschwindigkeit v in der Beschleunigung
enthalten ist, bietet sich ein iteratives Integrationsverfahren zur
Lösung der Differentialgleichung an. Wir verwenden das numerische
Eulersche Integrationsverfahren mit den Anfangswerten:
vx(t=0) = 1 m/s ; vy(t=0) = 0 m/s ; x(t=0) = 0 m ; z(t=0) = h = 5,30 m
Mit einer Schrittweite von 0,01s erhält man folgende Grafiken für die
Trajektorie sowie die Flugweite in Abhängigkeit von der Zeit:
Trajektorie Hörsaalversuch Magnuseffekt
7
6
5
z/m
4
3
2
1
0
0
2
4
6
x/m
8
10
Magnuseffekt mit Luftw iderstand
w aagerechter Wurf - Vakuum
Magnuseffekt Cw = 0
Trajektorie Experiment
Flugweite für C = 0,014
12
Strecke / m
10
8
6
4
2
0
0
0,5
1
1,5
2
2,5
3
t/s
mit Luftwiderstand
ohne Luftwiderstand
x(t) gemessen
3,5
Höhe für C = 0,014
7
6
Strecke / m
5
4
3
2
1
0
0
0,5
1
1,5
2
2,5
3
3,5
4
t/s
Höhe - z
y(t) gemessen
Cw=0
Die Grafiken verdeutlichen das experimentelle Resultat: Im Vergleich
zum einfachen waagerechten Wurf fliegt die Rolle weit in den Raum
hinein. Die Flugzeit von 3,4s entspricht einer Weite von etwa 7m,
während im freien Fall der Boden etwa nach einer Sekunde erreicht
würde (im Video ist ein deutliches Krachen nach 3,4s zu vernehmen).
Während der ersten Sekunde stimmt die schwach konkav gekrümmte
Flugbahn gut mit der ungedämpften „grünen“ Kurve überein.
Ohne Berücksichtigung des Luftwiderstandes würde sich die Rolle in
Form einer Zykloide durch den Raum bewegen und durch den
Auftrieb faktisch nicht an Höhe verlieren. Berücksichtigt man den
Luftwiderstand so erhält man statt der „grünen“ die „schwarze“ bzw.
„rote“ Trajektorie.
Die Konstante Cw (nicht cw) wurde mit Cw = 0,75m-1 angepasst.
Diesen Wert würde man in etwa erhalten, wenn man für cw =1 die
Terme für Druckwiderstand und Reibungswiderstand addiert.