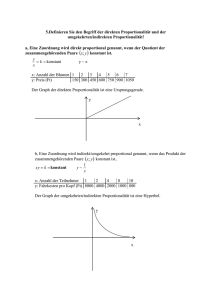
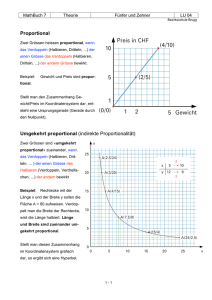
Direkte und indirekte Proportionalität

Direkte und indirekte Proportionalität
Sie kennen bereits viele Beispiele von Größen, die zueinander direkt oder indirekt proportional sind:
 Kauft man die doppelte Menge einer Ware, so verdoppelt sich auch der Preis (wenn es keinen Rabatt gibt).
Menge und Preis sind zueinander direkt proportional.
 Verdoppelt sich der tägliche Heizölverbrauch, so kommt man mit einer Tankfüllung nur halb so lang aus. Der
Verbrauch und die Zeitdauer, die man auskommt, sind zueinander indirekt proportional.
Mithilfe von Funktionen können wir solche Zusammenhänge jetzt noch genauer untersuchen.
Definition.
Zwei Größen und heißen (direkt) proportional zueinander, wenn es eine Zahl ( 0) gibt, sodass gilt:
⋅
Die Zahl heißt Proportionalitätsfaktor.
Zwei Größen und heißen indirekt proportional zueinander, wenn es eine Zahl ( 0) gibt, sodass gilt:
Fasst man diese Definitionen als Funktionsgleichungen auf, so erkennt man darin Spezialfälle einer linearen Funktion bzw. einer Potenzfunktion:
⋅
direkte Proportionalitätsfunktion
⋅ )
(bzw.
indirekte Proportionalitätsfunktion
Der Graph ist eine
Gerade durch den
Koordinatenursprung.
Es gilt:
Verdoppelt (verdreifacht, halbiert, …) sich die eine
Größe, dann verdoppelt (verdreifacht, halbiert, …) sich
auch die andere.
Der Graph ist
eine sogenannte
Hyperbel.
Es gilt:
Verdoppelt (verdreifacht, halbiert, …) sich die eine
Größe, dann halbiert (drittelt, verdoppelt, …) sich die
andere.
In der Praxis sind die Werte der Größen und fast immer positiv (Geldbeträge, Längen, Zeitspannen, Geschwindigkeiten, …). Daher sind die Funktionsgraphen auch nur im 1. Quadranten dargestellt.
3.01
ABC
a) Bei einer Bewegung mit gleichbleibender Geschwindigkeit ist die Länge s(t) des in der Zeit t
zurückgelegten Weges zu t direkt proportional.
(i) Drücken Sie diesen Zusammenhang durch
eine Gleichung aus und stellen Sie ihn grafisch dar.
(ii) Interpretieren Sie den Proportionalitätsfaktor
im Sachzusammenhang.
Lösung:
(i)
⋅
b) Die Schadstoffemission S einer Müllverbrennungsanlage ist indirekt proportional zum Quadrat der Verbrennungstemperatur T.
Um welchen Prozentsatz muss man die Temperatur erhöhen, wenn die Emission um 5 % sinken
soll?
Lösung:
Es gilt:
(mit einer noch nicht bekannten Zahl k)
Zu Beginn können wir sowohl die Emission, als
auch die Temperatur mit 100 % = 1 annehmen.
Also: 1
(ii) Aus dem eingezeichneten Steigungsdreieck
sieht man: Pro Zeiteinheit wird die Wegstrecke k zurückgelegt. Der Proportionalitätsfaktor gibt also die Geschwindigkeit an.
⇒
k
1
Die Emission um 5 % zu senken bedeutet, dass
sie statt 100 % nur noch 95 % beträgt.
Also: 0,95
⇒
1,0260
Man muss die Temperatur um 2,6 % erhöhen.
Aufgaben
3.02
AD
Erklären Sie, warum man Proportionalität auch auf
folgende Weise definieren kann:
3.07
D
Das Diagramm zeigt den Zusammenhang zwischen
der Temperaturangabe in Grad Celsius und in Grad
Fahrenheit. Argumentieren Sie anhand der Abbildung, ob es sich dabei um einen direkt proportionalen Zusammenhang handelt.
3.08
AB
Die Beleuchtungsstärke B eines Beamers ist indirekt proportional zum Quadrat der
Entfernung d von der beleuchteten Leinwand.
Berechnen Sie, um wie viel Prozent man die Entfernung verändern muss, um die Beleuchtungsstärke
auf das 1,3-Fache zu erhöhen.
Geben Sie an, ob es sich um eine Erhöhung oder
Verringerung der Entfernung handelt.
3.09
ABC
In einer Großküche sind 20 kg Reis auf Lager. Wenn
täglich Kilogramm verbraucht werden, kommt man
mit diesem Vorrat noch
Tage aus.
a) Stellen Sie eine Gleichung jener Funktion auf,
die die Zeit
in Abhängigkeit vom Tagesverbrauch angibt.
Zeichnen Sie den Graphen dieser Funktion in einem sinnvollen Definitionsbereich.
Beschreiben Sie die Eigenschaften des Funktionsgraphen.
b) Wie ändert sich die Zeit, die man mit dem Vorrat
auskommt, wenn sich der tägliche Verbrauch
verdoppelt?
c) Interpretieren Sie das Produkt ⋅
im Sachzusammenhang. Welchen Wert hat dieses Produkt?
d) Geben Sie einige Beispiele von Größen aus dem
Bereich Gastronomie an, die zueinander direkt
proportional sind.
3.10
AB
Nehmen Sie an, dass die Unfallhäufigkeit auf einem bestimmten Straßenstück direkt proportional
zum Quadrat der erlaubten Höchstgeschwindigkeit
ist.
Um wie viel Prozent müsste man die erlaubte
Höchstgeschwindigkeit senken, um die Unfallhäufigkeit zu halbieren?
3.11
BC
Ergänzen Sie die Tabelle so, dass und zueinander a) direkt, b) indirekt proportional sind.
a)
b)
1 2 3
1 2 3
8
8
alternative Definition.
Direkte Proportionalität besteht zwischen zwei Größen,
deren Quotient konstant ist.
Indirekte Proportionalität besteht zwischen zwei Größen,
deren Produkt konstant ist.
3.03
AB
3.04
AB
3.05
BCD
Eine bestimmte Ölheizung verbraucht bei maximaler
Leistung 1,45 Liter pro Stunde (L/h). In dieser Betriebseinstellung würde der verbleibende Heizölvorrat noch für 342 Stunden reichen.
Berechnen Sie, um wie viele Stunden sich die Betriebsdauer verändert, wenn der Verbrauch auf
1,2 L/h gesenkt wird.
Tipp: Am einfachsten ist die Berechnung, wenn Sie
die oben angegebene Definition verwenden.
In einer Textilfabrik kann ein bestimmter Arbeitsvorgang in 46 Arbeitsstunden erledigt werden, wenn 7
Maschinen im Einsatz sind.
Berechnen Sie, um wie viele Stunden und Minuten
sich die Fertigstellung verzögert, wenn nach 30 Stunden eine Maschine ausfällt.
Fällt ein Stein in die Tiefe, so ist sein zurückgelegter
Weg (in Metern) direkt proportional zum Quadrat
der Fallzeit (in Sekunden).
a) In 3 Sekunden hat ein Stein im freien Fall
44,1 Meter zurückgelegt. Welche Strecke hatte
er nach 2 Sekunden zurückgelegt?
b) Welcher der folgenden Graphen stellt den Zusammenhang von Zeit und zurückgelegtem
Weg richtig dar? Begründen Sie.
1
3.06
ABC
2
3
Die Kosten (in €)
für das Tapezieren eines Raumes
sind direkt proportional zur Wandfläche (in m²).
a) Interpretieren Sie die Bedeutung des Proportionalitätsfaktors im Sachzusammenhang.
b) Bei einer Wandfläche von 18 m² betragen die
Kosten bei einer bestimmten Tapete € 51.
Berechnen Sie die Kosten für eine Wandfläche
von 62 m².