Direkte Proportionalität - Hulda-Pankok

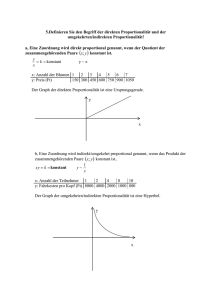
Grundwissen
Direkte Proportionalität
Theorie:
In der Physik lässt sich der Zusammenhang zwischen zwei Größen oft durch eine
Gesetzmäßigkeit beschreiben. Ein sehr einfacher Zusammenhang, der im PhysikAnfangsunterricht eine wichtige Rolle spielt, ist die direkte Proportionalität zwischen
zwei Größen.
Erkennungsmerkmale der direkten Proportionalität
a) Feststellen der Proportionalität anhand einer Messtabelle (Messreihe)
Beispiel:
1. Größe (x): Masse einer
100 200 300 400 500 600
Ware in g
2. Größe (y): Preis einer Ware
150 300 450 600 750 900
in DM
Festlegung:
Wenn zum Doppelten, Dreifachen, Vierfachen . . . .n-fachen der 1. Größe
das Doppelte, Dreifache, Vierfache. . . .der 2. Größe gehört,
so sind die beiden Größen zueinander direkt proportional.
Man erkennt diesen Zusammenhang am einfachsten, wenn man den Quotienten
zusammengehöriger Werte bildet. Ist dieser Quotient konstant, so sind die beiden
Größen zueinander direkt proportional.
Man sagt:
Direkt proportionale Größen sind quotientengleich
Für das obige Beispiel ergibt sich:
1. Größe (x): Masse einer Ware
100 200 300 400 500 600
in g
2. Größe (y): Preis einer Ware in
150 300 450 600 750 900
DM
Quotient y/x: Preis pro Masse in
1,50 1,50 1,50 1,50 1,50 1,50
DM/g
________________________________________________________________________________________________________________________
C:\Dokumente und Einstellungen\Heinz Gniostko\Eigene Dateien \Gniostko\Unterricht\KURSE\PH-11-1\PH11_GW_Proportionalität.doc
Seite 1 von 2
Schreibweise:
Sind zwei Größen x und y zueinander direkt proportional, so schreibt man:
y ~ x (sprich: y proportional x)
Wegen der Quotientengleichheit kann man auch schreiben:
Man bezeichnet C als Proportionalitätskonstante.
Gilt also y ~ x (1), so kann man durch Einführen der Proportionalitätskonstanten C
sofort die Gleichung y = C
________________________________________________________________________________________________________________________
C:\Dokumente und Einstellungen\Heinz Gniostko\Eigene Dateien \Gniostko\Unterricht\KURSE\PH-11-1\PH11_GW_Proportionalität.doc
Seite 2 von 2