Proportionale Zuordnungen

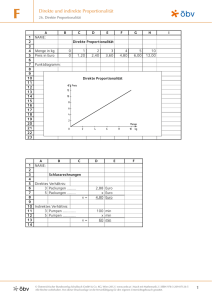
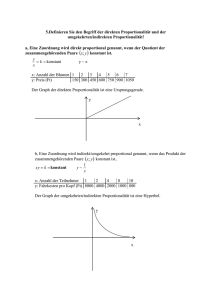
Proportionale Zuordnungen
1. Direkte Proportionalität
Bei einer direkten Proportionalität wird dem doppelten, dreifachen,...Wert der einen Größe, das doppelte,
dreifache,... der anderen Größe zugeordnet.
Man kann Sätze formulieren wie. Je mehr...., desto mehr
Bsp.:
Der Preis für Benzin in €:
Je mehr Benzin ich tanke, desto mehr muss ich bezahlen.
produzierte Gegenstände:
Je mehr Maschinen ich habe, desto mehr Teller produzieren diese.
oder
Je länger eine Maschine läuft, desto mehr Teller produzieren diese.
Dreisatz:
Bsp.: 7 l Diesel kosten 7,84 €, wie viel kosten 20 l Diesel.
Liter
7l
Preis
7,84 €
1l
1,12 €
:7
·20
20 l
22,40 €
20 l Diesel kosten 22,40 €.
oder kurz 7,84 : 7 · 20 = 22,40 €
Proportionale Zuordungen sind quotientengleich. Das heißt, wenn man den Quotienten aus den beiden Werten
eines Wertepaars bildet ist das Ergebnis immer gleich.
7,84: 7 = 1,12 und 22,40 : 20 = 1,12
2. Umgekehrte Proportionalität
Bei einer indirekten Proportionalität wird dem doppelten, dreifachen, ... Wert der einen Größe die Hälfte, der
dritte Teil,... der anderen Größe zugeordnet.
Man kann Sätze formulieren wie. Je mehr...., desto weniger
Bsp.:
Fahrt mit einem Auto:
Je schneller ich fahre (mehr Geschwindigkeit),
desto weniger Zeit benötige ich um Ziel.
produzierte Gegenstände:
Je mehr Maschinen ich habe, desto weniger Zeit benötigen diese
für einen festen Anzahl Teller.
Dreisatz:
Bsp.: 7 Maschinen brauchen 40 Stunden um 20000 Teller zu produzieren. Wie lange benötigen 5 Maschinen?
Maschinen
7l
Zeit
40 h€
1l
280 h
·7
:5
20 l
56 h
oder kurz 7 · 40 : 5 = 56 h
5 Maschinen benötigen 56 Stunden um 20000 Teller zu produzieren
Umgekehrt Proportionale Zuordungen sind produktgleich. Das heißt, wenn man den Produkte aus den
beiden Werten eines Wertepaars bildet ist das Ergebnis immer gleich.
7 · 40 = 280 und 5 · 56 = 280