Spektroskopische Entfernungsbestimmung - lehrer.uni
Werbung

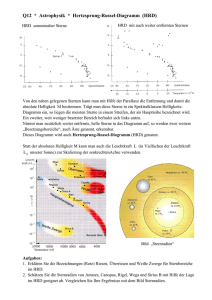
Spektroskopische Entfernungsbestimmung von Sternen oder Sternhaufen Sterne Jenseits der Reichweite derzeitiger trigonometrischer Parallaxen muss man sich anders behelfen. Wenn man aus irgendwelchen messbaren Eigenschaften eines Sterns - zum Beispiel aus seinem Spektrum - auf seine absolute Helligkeit M schließen kann, dann lässt sich daraus auch seine Entfernung ableiten, wenn man noch die scheinbare Helligkeit m im gleichen Spektralbereich misst. Solche Verfahren nennt man auch „photometrische Parallaxen", obwohl sie mit dem eigentlichen Verfahren der Parallaxenmessung nichts gemeinsam haben. Aus historischen Gründen werden in der Vermessung der Milchstraße die Begriffe Entfernung und Parallaxe häufig als Synonyme gebraucht. Zusätzlich zur gemessenen scheinbaren Helligkeit m und der aus dem Spektrum berechneten absoluten Helligkeit M benötigt man noch den Wert der interstellaren Extinktion A in der Sichtlinie zum Stern. Aus der Definition des Entfernungsmoduls folgt: d = 100,2⋅( m − M +5− A) pc = 10 pc ⋅100,2⋅( m − M − A) ≈ 10 pc ⋅1,585( m − M − A) Dieses Prinzip der photometrischen Parallaxe, d. h. eine Entfernungsbestimmung aus m und M, kann für alle Sterntypen benutzt werden, deren Charakteristika irgendwelche Hinweise auf ihre absolute Helligkeit liefern. Insbesondere erlaubt die detaillierte quantitative Spektralanalyse die Bestimmung einer Leuchtkraft und damit der Entfernung. Ein Problem bei allen photometrischen Verfahren ist die interstellare Extinktion A = ∆m . Diese gibt an, um welchen Betrag ∆m die dahinter liegenden Sterne abgeschwächt werden. Schon ein leichtes Abweichen der tatsächlichen Extinktion vom angenommenen Wert kann erhebliche Fehler in der Entfernungsbestimmung zur Folge haben. Als Faustregel gilt, dass in der erweiterten Sonnenumgebung für das visuelle Spektrum A ≈ 1 mag Extinktion pro 1 kpc Sichtlinie stattfindet. Praktisches Vorgehen: I. Bestimmung des Spektraltyps und der Leuchtkraftklasse eines Sterns II. Entnahme der absoluten Helligkeit M aus dem HRD / FHD III. Abschätzen der Extinktion IV. Berechnung der Entfernung Sternhaufen Bei Sternhaufen sieht das jeweilige FHD ähnlich zum HRD (FHD) der sonnennächsten Sterne aus. Die erkennbare Hauptreihe beim Sternhaufen ist jedoch gegenüber der Hauptreihe im HRD vertikal verschoben. Diese vertikale Verschiebung auf der Helligkeitsskala entspricht gerade dem Entfernungsmodul m − M . Praktisches Vorgehen: I. Ablesen der scheinbaren Helligkeit für bestimmtes B-V II. Entnahme der absoluten Helligkeit M eines Hauptreihensterns des selben Wertes für B-V aus dem FHD III. Abschätzen der Extinktion IV. Berechnung der Entfernung Spektroskopische Entfernungsbestimmung von Sternen oder Sternhaufen Aufgaben 1. Aus dem Spektrum des Sterns Alpha Centauri B lässt sich die Spektralklasse K1V ableiten. Außerdem beträgt seine Helligkeit im V-Band mV = 1.33, wobei die Extinktion vernachlässigbar ist. Schätze die Entfernung ab, wiederum durch Vergleich mit dem geeichten HRD. 2. Abbildung 1 zeigt das FHD des Sternhaufens NGC 6709 (Datenpunkte, mit einem Fit für die Hauptreihe). Mittels 3-Filter-Photometrie wurde die interstellare Verfärbung zu E(B −V ) = 0.35 und die Extinktion zu AV = 1.1 bestimmt. Bestimme durch den Vergleich mit dem geeichten HRD der Sonnenumgebung (Sterne mit bekannter Parallaxe, bestimmt mit HIPPARCOS) die Entfernung von NGC 6709. 3. Die Abbildungen 2 und 3 zeigen die FHD der Sternhaufen „Hyaden“ und Plejaden. Die Extinktion wurde zu AV = E ( B − V ) = 0, 003 ± 0, 002 bestimmt. Bestimme durch den Vergleich mit dem geeichten HRD die Entfernung der beiden Sternhaufen. Abbildung 1: FHD von NGC 6709 Spektroskopische Entfernungsbestimmung von Sternen oder Sternhaufen Abbildung 2: FHD der Hyaden http://www.aanda.org/index.php?option=article&access=standard&Itemid=129&url=/articles/aa/full/2002/02/aah3138/node4.html Abbildung 3: FHD der Hyaden und Plejaden http://homepage.mac.com/andjames/Page030b.htm Strahlungsgesetze, Leuchtkraft & Spektralanalyse Geeichtes HRD/FHD von sonnennahen Sternen http://commons.wikimedia.org/wiki/File:HRDiagram.png Autor Richard Powell auf Wikimedia Commons