Eingangstest

Name:
Tutoriumsnr.:
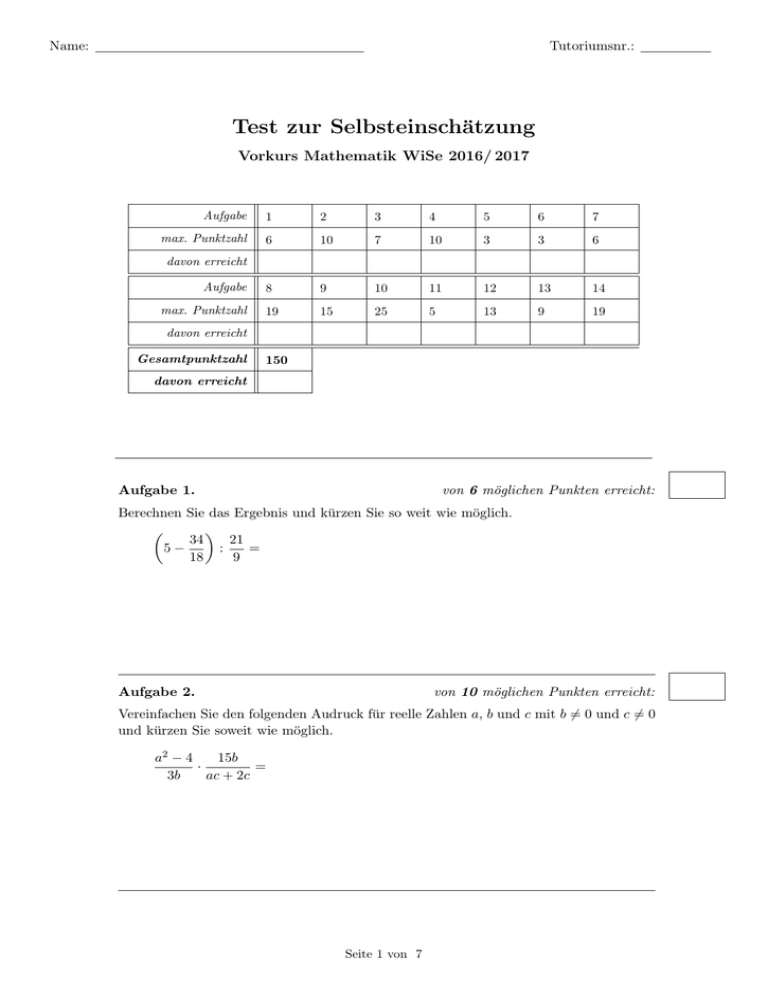
Test zur Selbsteinschätzung
Vorkurs Mathematik WiSe 2016/ 2017
Aufgabe
1
2
3
4
5
6
7
max. Punktzahl
6
10
7
10
3
3
6
8
9
10
11
12
13
14
19
15
25
5
13
9
19
davon erreicht
Aufgabe
max. Punktzahl
davon erreicht
Gesamtpunktzahl
150
davon erreicht
Aufgabe 1.
von 6 möglichen Punkten erreicht:
Berechnen Sie das Ergebnis und kürzen Sie so weit wie möglich.
34
21
5−
:
=
18
9
Aufgabe 2.
von 10 möglichen Punkten erreicht:
Vereinfachen Sie den folgenden Audruck für reelle Zahlen a, b und c mit b 6= 0 und c 6= 0
und kürzen Sie soweit wie möglich.
a2 − 4
15b
·
=
3b
ac + 2c
Seite 1 von 7
Name:
Tutoriumsnr.:
Aufgabe 3.
von 7 möglichen Punkten erreicht:
Vereinfachen Sie den folgenden Ausdruck für reelle Zahlen a, b und t mit a 6= 0 und
b 6= 0, indem Sie Potenzgesetze anwenden.
2
a4 5
(ab)
b−5 =
at b5
Aufgabe 4.
von 10 möglichen Punkten erreicht:
Vereinfachen Sie folgenden Ausdruck für die Funktion F für reelle Zahlen a, b. Hierbei
bezeichnet ln x“ den natürlichen Logarithmus von x, für x > 0. Welcher Wert ergibt
”
sich für F für a = 8 und b = −5?
a−b
F (a, b) = ln (9a ) + ln(9b )
=
ln 3
F (8, −5) =
Aufgabe 5.
von 3 möglichen Punkten erreicht:
c
·
a
γ
Betrachten Sie die folgende Skizze eines rechtwinkligen Dreiecks. Bekannt sind die Länge der Seite a sowie der Winkel γ.
Geben Sie an, wie aus diesen die Länge der Seite b berechnet
werden kann.
b
Seite 2 von 7
Name:
Tutoriumsnr.:
Aufgabe 6.
von 3 möglichen Punkten erreicht:
Vereinfachen Sie den folgenden Ausdruck.
− sin x · sin(−x) + cos x · cos(−x) =
Aufgabe 7.
von 6 möglichen Punkten erreicht:
Betrachten Sie die folgenden Skizzen: Die Vektoren ~a und ~b liegen in der schraffierten
Ebene. Ergänzen Sie die Skizzen jeweils. . .
~a
. . . um den Vektor ~a + ~b
0
~b
~a
. . . um den Vektor ~b − ~a
0
~b
~a
. . . um den Vektor ~a × ~b
0
Seite 3 von 7
~b
Name:
Tutoriumsnr.:
Aufgabe 8.
von 19 möglichen Punkten erreicht:
Führen Sie für x 6= 1 die Polynomdivision durch.
4x5 + 4x4 + 2x3 − 16x2 + 8x − 2 : (2x − 2) =
Aufgabe 9.
von 15 möglichen Punkten erreicht:
Geben Sie die Lösungsmenge L der folgenden Gleichung in x ∈ R an.
2x2 +
5
2x
3
−1=0
Seite 4 von 7
Name:
Tutoriumsnr.:
Aufgabe 10.
von 25 möglichen Punkten erreicht:
Lösen Sie das Gleichungssystem für reelle Zahlen a, b, c, indem Sie es zunächst auf
Stufenform (Gauß-Verfahren) bringen.
2a + 4b + 2c = 6,
a=
,
b=
a − 2b − 3c = −5,
,
3a − 2b − c = −11
c=
Aufgabe 11.
von 5 möglichen Punkten erreicht:
Geben Sie die erste Ableitung der folgenden Funktion f in R \ {0} an.
2
3
f (x) = x2 c −
3
x
df (x)
=
dx
Seite 5 von 7
Name:
Tutoriumsnr.:
Aufgabe 12.
von 13 möglichen Punkten erreicht:
Geben Sie die ersten zwei Ableitungen der folgenden Funktion g in R \ {0} an. Hierbei
steht exp x“ für ex für eine reelle Zahl x und e ist die Eulersche Zahl.
”
√
g(t) = − 9t + exp t2
dg(t)
=
dt
d2 g(t)
=
dt2
Aufgabe 13.
von 9 möglichen Punkten erreicht:
Berechnen Sie das Integral.
Z2 αt2 +
1
t2
dt =
1
Seite 6 von 7
Name:
Tutoriumsnr.:
Aufgabe 14.
von 19 möglichen Punkten erreicht:
Berechnen Sie das unbestimmte Integral. Hierbei steht exp x“ für ex für eine reelle Zahl
”
x und e ist die Eulersche Zahl.
Z
u · exp(cu) du =
Selbsteinschätzung.
Wie viele von 150 möglichen Punkten erwarten Sie in diesem Test zu erhalten?
0 – 30
31 – 60
61 – 90
91 – 120
121 – 150
Seite 7 von 7