FOS.PH.BY.88.AII

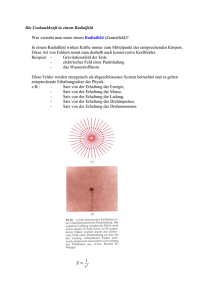
Abschlußprüfung an Fachoberschulen: Physik 1988
Aufgabe II
1.0
Eine geladene, isoliert aufgestellte Hohlkugel erzeugt in ihrer Umgebung ein elektrisches Feld.

1.1.1 In einem Versuch soll der Betrag der elektrischen Feldstärke E in Abhängigkeit von
der Ladung der Hohlkugel und von der Entfernung von ihrem Mittelpunkt untersucht
werden. Beschreiben Sie die Durchführung eines Versuchs. Geben Sie dabei die erforderlichen Geräte an.
1.2.0 In einem Teilversuch trägt die Kugel die Ladung Q1. Es wird der Zusammenhang
zwischen dem Betrag der Feldstärke E und der Entfernung r vom Kugelmittelpunkt
untersucht.
Dabei ergibt sich folgende Meßreihe:
Messung Nr.
1
2
3
4
r in cm
20
30
40
60
9,6
4,2
2,4
1,1
E in 103
N
C
1.2.1 Ermitteln Sie die Abhängigkeit der Feldstärke E von r12 durch graphische Auswertung
der Meßreihe für r  20 cm.
1.2.2 Geben Sie den Zusammenhang zwischen E und r in Form einer Gleichung an und
bestimmen Sie die auftretende Konstante k aus Ihrem Diagramm.
1.2.3 Ermitteln Sie aus der Konstanten k die felderzeugende Ladung Q1 der Kugel.
1.3.0 Die Hohlkugel trägt die Ladung Q1 = + 4,2  10 –8 C. In ihr elektrisches Feld wird die
punktförmige Ladung Qp = –1,7  10 –10 C gebracht, die sich vom Punkt P 1 (Entfernung
r1 = 54 cm vom Kugelmittelpunkt) bis zum Punkt P 2 (Entfernung r2 = 42 cm vom Kugelmittelpunkt) frei bewegen kann.
1.3.1 Berechnen Sie die Potentialdifferenz zwischen P1 und P2.
1.3.2 Ermitteln Sie rechnerisch, welche Änderung  W der potentiellen Energie die Ladung
Qp während der Bewegung von P 1 nach P2 erfährt.
2.1.0 Elektronen werden mit der Geschwindigkeit


v 0 senkrecht zur Flußdichte B in ein homogenes Magnetfeld eingeschossen (s. Skizze).
m
Dabei gilt: B = 2,5 mT; v0 = 1,8  107
s
Die Anordnung befindet sich im Vakuum.
88-6

B

v0
2.1.1 Berechnen Sie die Beträge der Kräfte, die auf ein Elektron innerhalb des Magnetfeldes
wirken, und zeigen Sie, daß die Gravitationskraft der Erde vernachlässigbar ist.
2.1.2 Begründen Sie, daß die Elektronen innerhalb des homogenen Magnetfeldes einen
Kreisbogen durchlaufen.
2.1.3 Berechnen Sie den Radius r dieses Kreisbogens.
2.2.0 Dem homogenen Magnetfeld von 2.1.0 soll nun ein homogenes
elektrisches Feld der
art überlagert werden, daß die mit der Geschwindigkeit v 0 eingeschossenen Elektronen
keine Ablenkung erfahren.
2.2.1 Geben Sie in einer Skizze die auf ein Elektron wirkenden Kräfte an. Tragen Sie auch

die Richtung der elektrischen Feldstärke E ein.

2.2.2 Berechnen Sie den Betrag von E .

2.2.3 Was geschieht mit Elektronen, die mit einer höheren Geschwindigkeit v1 auf gleiche
Weise in die Anordnung von 2.2.0 eingeschossen werden?
Begründen Sie Ihre Aussage.
Lösung
1.1.1 An Geräten sind erforderlich:
– isoliert aufgestellte Hohlkugel
– Ladungsquelle (z. B. Bandgenerator)
– Meßgerät für Ladungen (z. B. Meßverstärker)
– Meßgerät für elektrische Feldstärken (Elektrofeldmeter)
– Maßstab zur Entfernungsmessung
Versuchsdurchführung:
Es sind zwei Meßreihen erforderlich, da die Abhängigkeit des Betrags der elektrischen
Feldstärke sowohl vom Abstand r zum Kugelmittelpunkt als auch von der Ladung Q
der Kugel bestimmt werden soll.
1. Meßreihe (Q = konstant)
Mit dem Elektrofeldmeter mißt man den Betrag der elektrischen Feldstärke in verschiedenen Abständen zum Kugelmittelpunkt. Man erhält E (r).
2. Meßreihe (r = konstant)
Der Abstand des Elektrofeldmeters zum Kugelmittelpunkt wird fest gewählt und die

Kugelladung Q verändert. Mit dem Elektrofeldmeter mißt man | E | , mit dem Meßverstärker Q. Man erhält E (Q).
1.2.1 Aus der Meßreihe erhält man für die Graphik:
1
1
in 2
r2
m
25
11
6,3
2,8
N
C
9,6
4,2
2,4
1,1
E in 103
88-7
N
C
E in 103
10
9
8
7
6
 E
5
4
3
2
1
 ( r2 )
1
0
5
0
10
15
20
25
1
in m–2
r2
Der Graph ist Teil einer Ursprungsgeraden. Es gilt also:
1
E~
r2
1.2.2 Aus der Proportionalität folgt:
1
E  k
r2
Die Konstante k ist der Steigungsfaktor der Geraden. Man erhält aus der Graphik:

 r1   15 m
2
2
N
C
5,8  10 3 N
E
C
k

2
1
15
m
 2
 E  5,8  10 3

r 
k  3, 9  10 2
N m2
C
1.2.3 Für die Feldstärke E in einem radialen Feld mit der felderzeugenden Ladung Q1 gilt:
Q
1
E
 1
4  0 r 2
88-8
Der Vergleich mit 1.2.2 liefert:
Q
k 1
4 0

Q1  4 0 k
N m2
C
 3, 9  10 2
Vm
C
V As
Nm
 Nm

J
 4, 3  10 8 As 1
1 1
 1 As 
V
V
V
 V

Q1  4  8, 85  10 12
Q1  4, 3  10 8
1.3.1 Wählt man den Bezugspunkt im Unendlichen, so wird das Potential beschrieben durch:
Q
1
 (P) 
 1
4  0 r
Für die Potentialdifferenz ergibt sich dann:
   (P2 )   (P1)
 
 1 1
1
 Q1   
4 0
 r2 r1 
 
1
4  8,85  10 12
 1
1 
 4, 2  10 8 As  


 0, 42 m 0,54 m 
As
Vm
  2, 0  10 2 V
1.3.2 Es gilt:
 W = Epot (P2) – Epot (P1)
 W =  (P2)  Qp –  (P1)  Qp
 W = ( (P2) –  (P1))  Qp
 W =    Qp
W  2, 0  10 2 V  (1, 7  10 10 As)
W  3, 4  10 8 J


2.1.1 Wegen v 0  B gilt für den Betrag der Lorentzkraft:
FL  e  v  B

FL  1, 6  10 19 As  1, 8  10 7
FL  7, 2  10 15 N
m
Vs
 2, 5  10 3
s
m2
Für die Gravitationskraft ergibt sich:
FG  m  g

FG  9,11  10 31 kg  9, 81
FG  8, 94  10 30 N
m
s2
Die Gravitationskraft kann vernachlässigt werden, da FG << FL.
88-9
2.1.2 Für die auf ein Elektron wirkende Lorentzkraft gilt in vektorieller Schreibweise:

 
F L  e  v  B
wobei stets gilt:


Eigenschaften des Vektorprodukts


 
F L e vB sin( (v, B)) 



FL  v  FL  B
Damit folgt:




– Wegen F L  B und v 0  B (Voraussetzung aus 2.1.0) gibt es keine Komponente


des Vektors v in Richtung von B

 die Elektronen bewegen sich in einer Ebene senkrecht zu B
 
(d. h. es ist stets v  B ).


– Wegen F L  v ändert sich der Betrag der Geschwindigkeit nicht


 
– aus | v | = konstant, | B | = konstant und v  B folgt, daß der Betrag der Lorentzkraft
konstant bleibt.

 F L ist eine dem Betrage nach konstante
Kraft, die auf der momentanen Geschwin

digkeit v stets senkrecht steht. F L ist Zentralkraft, die Bahn ist eine Kreisbahn.
2.1.3 Es gilt nach 2.1.2:
FL  Fz
m  v2
evB 
r
mv
r

eB

r
e
m
v
B
1, 8  10 7
1, 76  1011 As
 2, 5  10 3
kg
r  4,1 cm
2.2.1

FC

B
e–
m
s

v
0

E

FL
88-10
Vs
m2
2.2.2 Nach 2.2.1 gilt:

FC  FL
eE  evB
E  vB
m
Vs
 2, 5  10 3
s
m2
V
E  4, 5  10 4
m
E  1, 8  10 7
2.2.3 Die Coulombkraft FC = e  E hängt nicht von der Geschwindigkeit ab, sie bleibt konstant.
Die Lorentzkraft FL = e  v  B ist proportional zu v.
Aus v1 > v0 folgt also: FL > FC.

Die Elektronen würden nach unten (in Richtung FL ) abgelenkt.
88-11