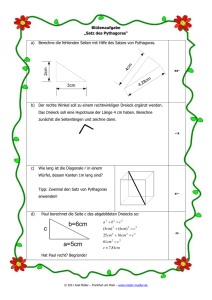
a 2 + b 2 = c 2

Der Satz des Pythagoras
2
a
+
2
b
=
2
c
Der nach Pythagoras von Samos benannte Satz ist theoretischer Ausdruck
der von indischen, babylonischen und ägyptischen Baumeistern und Priestern
entwickelten praktischen Kunst, bei Abmessungen von Feldern und
Bauten mit Hilfe von Seilen präzise rechte Winkel zu erzielen.
Der Satz des Pythagoras
2
a
+
2
b
=
2
c
Der nach Pythagoras von Samos benannte Satz ist theoretischer Ausdruck der
von indischen, babylonischen und ägyptischen Baumeistern und Priestern
entwickelten praktischen Kunst, bei Abmessungen von Feldern und Bauten
mit Hilfe von Seilen präzise rechte Winkel zu erzielen.
Umgekehrt kann man damit in rechtwinkligen Dreiecken die Länge der
3. Seite errechnen, wenn man die Länge der beiden anderen Seiten kennt.
Der Satz des Pythagoras
Rechtwinkliges
2
a
+
2
b
=
2
c
Dreieck ?
Der nach Pythagoras von Samos benannte Satz ist theoretischer Ausdruck der
von indischen, babylonischen und ägyptischen Baumeistern und Priestern
entwickelten praktischen Kunst, bei Abmessungen von Feldern und Bauten
mit Hilfe von Seilen präzise rechte Winkel zu erzielen.
Umgekehrt kann man damit in rechtwinkligen Dreiecken die Länge der
3. Seite errechnen, wenn man die Länge der beiden anderen Seiten kennt.
… und Es
einige
sindviele
rechtwinklig.
gibtdavon
unendlich
Dreiecke ….
… und einige davon sind rechtwinklig.
Die Seite c liegt dem rechten Winkel gegenüber …
c
… und ist die längste Seite.
a
b
Die Seiten …
a und
bildendavon
den rechten
Winkel (90°)
undbeinige
sind rechtwinklig.
Und a2 … ?
Die Seite c liegt dem rechten Winkel gegenüber …
a
*a=
c
a2
… und ist die längste Seite.
a
b
DieQuadrat
Seiten …
a und
beinige
bilden
den rechten
Winkel
und
sind rechtwinklig.
… ist ein
mit
der davon
Seitenlänge
a ! (90°)
Und b2 … ?
c
a
b
… ist ein Quadrat mit der Seitenlänge b !
Und zusammen
sind die Flächen
a2 + b2 …
c
a
b
… genau so groß wie die Fläche c2 !
Echt?
=c2
a2
c
a
b
+b2
Ja, sieh Dir das
Gitternetz an:
=c2
a2
+b2
Ja, sieh Dir das
Gitternetz an:
=c2
a2
+b2
Ja, sieh Dir das
Gitternetz an:
=c2
a2
Siehst Du, dass dieses
Quadrat aus 4 von
diesen Dreiecken
besteht?
+b2
Ja, sieh Dir das
Gitternetz an:
=c2
a2
Siehst Du, dass dieses
DieQuadrat
packen aus
wir jetzt
4 vonmal
indiesen
das rote
Quadrat!
Dreiecken
besteht?
+b2
Ja, sieh Dir das
Gitternetz an:
=c2
a2
+b2
Und jetzt noch die Teile
von a2 …
Ja, sieh Dir das
Gitternetz an:
=c2
a2
+b2
Und jetzt noch die Teile
von a2 …
Ja, sieh Dir das
Gitternetz an:
=c2
a2
+b2
Und jetzt noch die Teile
von a2 …
Ja, sieh Dir das
Gitternetz an:
=c22
=c
aa22
+b22
+b
Passt genau!
Ja, sieh Dir das
Gitternetz an:
2 2
=c
=c
a2
a2
+b22
+b
Passt genau!
Die Summe der Quadrate über den kurzen Seiten im
rechtwinkligen Dreieck ist so groß wie die Fläche des
Quadrates über der langen Seite!
2 2
=c
=c
a2
a2
+b22
+b
a2 + b2 = c2
Die Summe der Quadrate über den kurzen Seiten im
rechtwinkligen Dreieck ist so groß wie die Fläche des
Quadrates über der langen Seite!
Was nützt
uns dieses
Wissen ?
=c2
a2
+b2
a2 + b2 = c2
Wenn wir 2 Seiten eines rechtwinkligen Dreiecks kennen,
können wir die 3. ausrechnen:
=c2
a2
+b2
a2 + b2 = c2
Kennen wir a und b, dann gilt
und c ist dann die Wurzel aus dieser Summe.
=c2
a2
+b2
a2 + b2 = c2
Kennen wir a und c, dann gilt
und b ist dann die Wurzel aus dieser Differenz.
=c2
a2
+b2
c2 - a2 = b2
Kennen wir a und c, dann gilt
und b ist dann die Wurzel aus dieser Differenz.
=c2
a2
+b2
c2 - a2 = b2
Kennen wir b und c, dann gilt
und a ist dann die Wurzel aus dieser Differenz.
=c2
a2
+b2
c2 - b2 = a2
Kennen wir b und c, dann gilt
und a ist dann die Wurzel aus dieser Differenz.
Das können
wir, weil wir
=c
a
wissen
:
2
2
2
a
+
2
b
+b2
von Pythagoras!
=
2
c