"Wärmespeicher" - Leseprobe

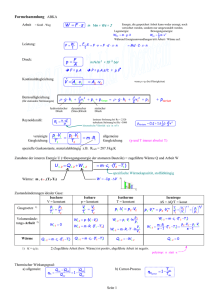
Leseprobe
Mit
=> Inhaltsverzeichnis + Kapitel 1 und 2
Die Graphiken sind in reduzierter Auflösung
und der Text ist nicht ausdruckbar
Hat Sie die Leseprobe überzeugt?
Dann profitieren Sie vom kompletten Buch
für nur 15,50 Euro zzgl. Versand.
Eine Bestellmöglichkeit finden Sie hier.
Inhalt
1
1.1
1.2
Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Warum Wärmespeicherung? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Arten von Wärmespeichern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2
2.1
2.2
2.3
2.4
2.5
Physikalische Grundlagen der Wärmespeicherung . . . . . . . . . . . . . . . . . . . .
Was ist Wärmespeicherung? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sensible Wärme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Latente Wärme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chemische Wärmespeicherung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wärmeverluste von Wärmespeichern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
10
11
13
16
18
3
3.1
3.2
3.3
Bau und Einsatz von Wärmespeichern, Wärmespeichermaterialien . . . . .
Kriterien für die Auswahl der Materialien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kriterien für den Bau von Wärmespeichern . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Beurteilung von Wärmespeichern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
22
25
28
4
4.1
4.2
4.3
4.4
4.5
4.6
4.7
Wasserwärmespeicher . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wasser als Speichermedium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bauarten von Wasserwärmespeichern zur Kurzzeitspeicherung . . . . . . . . . . . .
Schichtung in Wasserwärmespeichern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Warmwasser- und Pufferspeicher in Heizanlagen . . . . . . . . . . . . . . . . . . . . . . . .
Wärmespeicher in Solaranlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Einfluss von Wärmespeichern auf die Systemeffizienz . . . . . . . . . . . . . . . . . . . .
Der Speicher als „Wärmemanagementzentrale“ . . . . . . . . . . . . . . . . . . . . . . . . .
30
30
30
37
41
45
60
67
5
5.1
5.2
5.3
Langzeit-Wärmespeicher im Niedertemperaturbereich . . . . . . . . . . . . . . . .
Einsatzgebiete . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Speicherkonzepte zur Langzeit-Wärmespeicherung . . . . . . . . . . . . . . . . . . . . . .
Langzeitwärmespeicherung – realisierte Pilotprojekte in Deutschland . . . . . . .
69
69
70
74
6
6.1
6.2
Hochtemperatur-Wärmespeicher für Industrie und Solarkraftwerke . . . . 86
Einsatzbereiche und -beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Speichermedien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
7
Wärme- und Kältespeicherung in Bauteilen und im Gründungsbereich zur
Klimatisierung von Gebäuden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
Wärme- und Kältespeicherung in Bauteilen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
Wärme- und Kältespeicherung im Gründungsbereich von Gebäuden . . . . . . . 96
7.1
7.2
3
Inhalt
8
8.1
8.2
8.3
8.4
Betrachtungen zur Wirtschaftlichkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Berechnungsmethoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Warmwasserspeicher gegenüber Durchlauferhitzer . . . . . . . . . . . . . . . . . . . . . .
Wirtschaftlichkeitsvergleich von kleinen Solaranlagen . . . . . . . . . . . . . . . . . . .
Große Solaranlagen mit Kurz- und Langzeit-Wärmespeicher . . . . . . . . . . . . .
9
9.1
9.2
Zitierte Literatur und Abbildungsverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . 112
Zitierte Literatur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
Abbildungsverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
10
10.1
10.2
Laufende und abgeschlossene Forschungsvorhaben aus der
Energieforschung der Bundesregierung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
Laufende und kürzlich abgeschlossene Forschungsvorhaben . . . . . . . . . . . . . . 118
Forschungsberichte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
11
Weiterführende Literatur
12
Anschrift der Autoren
4
106
106
107
107
109
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
Vorwort
Wärmespeicher ermöglichen es, das Wärmeangebot im Zeitverlauf und in der Leistung dem
Bedarf anzupassen. Erst durch Wärmespeicher lassen sich viele Energiequellen wie Sonnenenergie oder industrielle Abwärme effizient nutzen. Auch im Bereich der Versorgungssicherheit und beim Wärmetransport spielen sie eine wichtige Rolle.
Wärmespeicherung umfasst ein sehr weites und sehr vielschichtiges Feld. Es reicht vom
Warmwasserspeicher, der in fast jeder Wohnung vorhanden ist und über den sich kaum noch
jemand Gedanken macht, bis hin zu riesigen Langzeit-Wärmespeichern für Niedertemperaturwärme und zu Hochtemperatur-Wärmespeichern für Temperaturen von fast 1.000 °C,
die dem Bereich „High Tech“ zugeordnet werden. Gemeinsam ist allen Wärmespeichern, dass
dem Vorgang „Wärmespeicherung“ physikalische Gesetze zugrunde liegen, die zum großen
Teil aus dem täglichen Leben bekannt sind.
Mit dem Informationspaket „Wärmespeicher“ soll aufgezeigt werden, welche Arten von
Wärmespeichern heute im Einsatz sind und welche kurz- und mittelfristig dazu beitragen
können, Wärme rationeller, d. h. mit weniger Einsatz an Primärenergie, zu nutzen. Die Darstellung und Erläuterung der physikalischen Grundlagen der Wärmespeicherung nimmt einen
relativ breiten Raum ein, da nach Ansicht der Autoren bei der Vielfalt des Themas nur so ein
roter Faden geschaffen werden kann, der durch die anschließenden exemplarischen Darstellungen hindurchführt.
Das Buch spiegelt die rasante Entwicklung wider, die in den letzten Jahren auf einigen
Gebieten stattgefunden hat. Als Beispiel seien hier die so genannten Solarspeicher genannt,
die speziell für diesen Anwendungsfall entwickelt wurden, während die früheren Speicher
lediglich modifizierte Speicher aus der Heiztechnik waren. Ein weiteres Beispiel sind Langzeit-Wärmespeicher zur saisonalen Speicherung von Solarwärme vom Sommer in den Winter, die in diesem Zeitraum den Weg von der Idee über die Planung bis hin zu Bau und Inbetriebnahme gegangen sind. Die vorliegende erweiterte und überarbeitete 4. Auflage des Buches
wurde um ein Kapitel ergänzt, das Klimatisierungskonzepte für Gebäude fokussiert, bei denen
die Wärme- und Kältespeicherung in Bauteilen und im Gründungsbereich genutzt wird.
Fachinformationszentrum Karlsruhe GmbH
Gesellschaft für wissenschaftlich-technische Information mbH
BINE Informationsdienst
5
1 Grundlagen
1.1 Warum Wärmespeicherung?
Wärmespeicher werden häufig im Zusammenhang mit der Nutzung neuer Energien und
rationellem Energieeinsatz genannt. Obwohl sie manchmal so bezeichnet werden, sind Wärmespeicher keine „Energiequellen“ – sie sind sogar Systemkomponenten, die Wärme verlieren – sie helfen lediglich, Energie und Anlagen effektiver zu nutzen, und tragen damit zu
einer Einsparung von Primärenergie bei. Ein alltägliches Beispiel dafür ist die Brauchwassererwärmung. Um heißes Wasser in einem Durchlauferhitzer aufzuheizen, ist kurzzeitig eine
hohe Wärmeleistung (ca. 20 kW) notwenig, die insgesamt jedoch nur eine halbe Stunde am
Tag benötigt wird. Wenn die Warmwasserbereitung mit elektrischer Energie erfolgt, bedeutet
dies, dass entsprechend Kraftwerkskapazität bereitstehen muss, da elektrische Energie nur
mit hohem Aufwand gespeichert werden kann. Heißes Wasser in einem wärmegedämmten
Behälter ist dagegen problemlos zu speichern, und mit Hilfe eines solchen einfachen Warmwasserspeichers lässt sich die Heizleistung auf 1–2 kW reduzieren und damit Kraftwerksund Leitungskapazität einsparen. Die Aufheizung solcher Speicher lässt sich durch eine entsprechende Steuerung auch leicht in Zeiten verlegen, in denen sonst wenig elektrische Energie benötigt wird (z. B. nachts). In diesem Beispiel steht eindeutig die rationellere Nutzung
von Anlagen im Vordergrund, die oft jedoch auch mit einem geringeren Einsatz an Primärenergie verbunden ist.
Ein weiteres Beispiel ist der Einsatz von großen Speichern in Fernwärmenetzen, die aus
Kraftwerken gespeist werden. Die kombinierte Erzeugung von elektrischer Energie und
Wärme ist eines der primärenergetisch günstigsten Verfahren rationeller Energienutzung
überhaupt, da hier ein großer Teil der bei der Stromerzeugung in Wärmekraftwerken anfallenden Abwärme genutzt werden kann. Da die Fernwärme jedoch mit einer höheren Temperatur als die übliche Abwärme benötigt wird, geht die elektrische Leistung des Kraftwerks etwas
zurück. Der Strombedarf weist morgens und abends während ein bis zwei Stunden Spitzen
auf, für deren Deckung teure Spitzenlastkraftwerke eingesetzt werden müssen. Wenn in diesen Zeiten die Wärmeproduktion eingestellt wird, lässt sich die Stromerzeugung der Kraftwerke steigern und man kann auf den Bau von Spitzenlastkraftwerken zum Teil verzichten.
Die Wärmeversorgung wird während dieser Zeit aus großen Speichern gedeckt, deren Installation billiger ist als die eines Kraftwerks. Je nach Struktur der Wärmeversorgung können solche Speicher auch dazu dienen, die Abwärme aus Kraftwerken zu speichern, die nur wenige
Stunden am Tag betrieben werden und deren Wärme zu dieser Zeit nicht benötigt wird. Die
Wärme wird dann später an das Fernheiznetz abgegeben.
6
Warum Wärmespeicherung?
Eglob
θaussen
QWV
Solare Einstrahlung (Globalstrahlung)
Umgebungstemperatur
Gesamtwärmebedarf als
Summe des Wärmebedarfs für Raumheizung
(QRH) und für Warmwasserbereitung (QWW)
Abb. 1: Solarstrahlung, Umgebungstemperatur (oben)
und Wärmebedarf für Heizung und Warmwasserbereitung (unten) eines
Hauses während zweier
Tage im Oktober (Qh,a =
30 kWh/(m2 ⋅ a))
Aufgrund der Verschiebung von Strahlungsenergieangebot und Wärmebedarf zur Warmwasserbereitung und Heizung stellt ein Wärmespeicher einen zentralen Baustein in thermischen Solaranlagen dar. In Abb. 1 ist der Verlauf von Solarstrahlungsangebot (links) und
Heizwärmebedarf eines Gebäudes während zweier Tage dargestellt. Der Heizwärmebedarf
(rechts im Bild) nimmt aufgrund der durch die Fensterflächen in das Gebäude als solare Wärmegewinne eintretenden Solarstrahlung ab.
In der Kollektoranlage wird die Solarstrahlung absorbiert und in Wärmeenergie umgewandelt. Über ein Rohrleitungsnetz gelangt die Wärme über einen Wärmeübertrager in den
Speicher. Die anschließende Entladung des Speichers erfolgt in Abhängigkeit des auftretenden Bedarfs. Während bei Solaranlagen zur Warmwasserbereitung ein nutzerabhängiges und
relativ konstantes Entnahmeprofil vorliegt, ist der Wärmebedarf bei solarunterstützter Heizung abhängig von der Witterung. Bei Nutzung der Solaranlage zur Heizungsunterstützung
muss diese zu Zeiten mit hohem Strahlungsenergieangebot ihre Wärme in einen Speicher liefern, aus dem dann am Abend und am nächsten Morgen das Gebäude beheizt werden kann.
Die saisonale Verteilung von Solarenergieangebot und Wärmebedarf eines Gebäudes ist in
Abb. 2 dargestellt.
7
1.500
200
Heizung [kWh]
Warmwasser [kWh]
1.200
160
Globalstrahlung [kWh/m2]
900
120
600
80
300
40
0
Globalstrahlung [kWh/m2]
Abb. 2: Saisonale Verteilung von
Solarenergieangebot und
Wärmebedarf für die
Raumheizung und Warmwasserbereitung eines
Wohngebäudes (Simulationsergebnisse für
ein Gebäude mit Qh,a =
30 kWh/(m2⋅a), ANutz =
122 m2, Standort Ulm)
Wärmebedarf [kWh/Monat]
Grundlagen
0
Jan
Feb
Mrz
Apr
Mai
Jun
Jul
Aug
Sep
Okt
Nov
Dez
Monat
Abb. 3: Solarer Deckungsanteil
einer 10 m2 großen Solaranlage für ein Gebäude mit
ca. 120 m2 Nutzfläche bei
unterschiedlichem Wärmedämmstandard
Bestand
12 %
Bestand
WSVO 1995
EnEV
PH
…
…
…
…
QRH
QRH
QRH
QRH
∼
∼
∼
<
250
80
60
15
kWh/(m2a)
kWh/(m2a)
kWh/(m2a)
kWh/(m2a)
15–20 %
WSVO 1995
20–25 %
EnEV
50–60 %
Passivhäuser
0
10
20
30
40
50
60
70
Solarer Deckungsanteil [%]
Je nach Wärmebedarf des zu versorgenden Gebäudes und Auslegung der Solaranlage
können bei Verwendung von Kurzzeit-Wärmespeichern in Niedrigenergie-Gebäuden solare
Deckungsanteile von etwa 25 % und in Gebäuden mit hohem Wärmeschutzstandard (Passivhäusern) Deckungsanteile von ca. 50 % erreicht werden (siehe Abb. 3).
Im Gegensatz zu Kurzzeit-Wärmespeichern mit der Wärmespeicherung über einige Tage
kann mit dem Einsatz von Langzeit-Wärmespeichern solare Wärme in den Sommermonaten
eingespeichert und in der Übergangszeit und im Winter zur Wärmeversorgung von Gebäuden genutzt werden. Abb. 2 zeigt den jährlichen Verlauf des Heizwärmebedarfs eines Hauses
und der Solarstrahlung auf die horizontale Fläche. Etwa zwei Drittel der Solarstrahlung treten in den Monaten von Mai bis Oktober auf, in denen nur knapp 25 % der Heizwärme (einschließlich Warmwasser) benötigt werden. Wenn man eine Solaranlage für den Heizbetrieb
im Januar auslegt, erhält man sehr große Kollektorflächen, die im Sommer viel Wärmeüberschuss produzieren und damit sehr unwirtschaftlich arbeiten. Eine Erhöhung des Speichervolumens in Langzeit-Wärmespeichern führt hier zur Reduzierung der erforderlichen Kollektorflächen und über die Entladung des Speichers zum Zeitpunkt des Wärmebedarfs in der
Heizperiode zur Erhöhung des solaren Deckungsanteils.
8
Arten von Wärmespeichern
Abb. 4: Einteilung der Wärmespeicher
1.2 Arten von Wärmespeichern
Wärmespeicher können hinsichtlich verschiedener Kriterien klassifiziert werden:
❏ nach der Temperatur in Nieder-, Mittel- und Hochtemperaturspeicher,
❏ nach der Dauer der Wärmespeicherung in Kurz- oder Langzeit-Wärmespeicher,
❏ nach dem physikalischen Prinzip in fühlbare, latente und chemische Speicher,
❏ nach dem Speichermedium z. B. in Wasserspeicher, Gesteinsspeicher.
In den folgenden Abschnitten soll primär nach den physikalischen Prinzipien der Wärmespeicherung (Abb. 4) unterschieden werden, die im nächsten Kapitel eingehend erläutert
werden. Zu den Speichern für fühlbare Wärme, in denen Wärmeenergie über eine Temperaturerhöhung des Mediums gespeichert wird, zählen die meisten der heute im Einsatz befindlichen Wärmespeicher, wobei die Speichermedien Wasser und Gestein dominieren. Speicher
für latente Wärme, in denen die Schmelz- oder Verdampfungswärme eines Mediums genutzt
wird, werden bei Anforderungen an eine hohe Energiedichte bzw. an eine Ein- und Ausspeicherung bei nahezu demselben Temperaturniveau eingesetzt. Im Vergleich zur Speicherung
fühlbarer Wärme spielt dieses Speicherprinzip jedoch aufgrund wirtschaftlicher und ökologischer Kriterien eher eine untergeordnete Rolle. Chemische Energiespeicher (z. B. auch in Form
fossiler Energieträger) arbeiten in der Regel auf höheren Temperaturniveaus und finden im
Bereich der Wärmeversorgung von Gebäuden kaum Anwendung.
9
2 Physikalische Grundlagen der Wärmespeicherung
2.1 Was ist Wärmespeicherung?
In der Thermodynamik (Wärmelehre) wird unter „Wärme“ eine über eine Systemgrenze
transportierte thermische Energie verstanden. Die Systemgrenze kann z. B. ein Heizkörper
sein, der Wärme an einen Raum abgibt. Wärme stellt demnach eine Vorgangs- oder Prozessgröße dar. Die thermische Energie ist immer an einen Stoff gebunden. Sie wird in der Thermodynamik mit „Innere Energie“ oder „Enthalpie“ bezeichnet. Im Beispiel führt die Wärmeabgabe des Heizkörpers zu einer höheren Enthalpie der Raumluft (bzw. einem Anstieg der
Raumlufttemperatur). Im allgemeinen Sprachgebrauch wird thermische Energie gleichbedeutend mit Wärme genutzt. Im Folgenden soll dieser allgemeine Sprachgebrauch, der sich auch
in der Fachsprache eingebürgert hat, beibehalten werden.
Für die Wärmespeicherung gilt:
Wärme kann nur als Enthalpie gespeichert werden.
Mit der Wärme muss immer auch ein Stoff gespeichert werden, der sie enthält.
Im Wesentlichen werden drei physikalische Prinzipien der Wärmespeicherung unterschieden:
❏ Speicherung fühlbarer oder sensibler Wärme infolge einer Temperaturänderung,
❏ Speicherung latenter Wärme durch Änderung des Aggregatzustandes (ohne Änderung
der Temperatur),
❏ Speicherung chemischer Wärme als Bindungsenergie bei Stoffreaktionen.
Bevor diese drei Prinzipien näher vorgestellt werden, sollen einige wichtige Begriffe eingeführt und erläutert werden:
Wärmeträgermedium ist der Stoff, der die Wärme in den Speicher transportiert und an das
Wärmespeichermedium abgibt.
Wärmespeichermedium ist das Medium, das die Wärme im Speicher selbst aufnimmt. Das
Wärmespeichermedium und das Wärmeträgermedium können identisch sein.
Wärmespeichervermögen ist die Wärmemenge, die ein Speicher aufnehmen kann. In der
Regel wird das Wärmespeichervermögen immer zusammen mit dem nutzbaren Temperaturbereich angegeben; als Abkürzung wird QSP verwendet. Die Einheiten kWh, MWh, kJ oder MJ
sind gebräuchlich; folgende Umrechnungen gelten:
10
Sensible Wärme
1 Megajoule (MJ) = 1.000 Kilojoule (kJ)
1 Megawattstunde (MWh) = 1.000 Kilowattstunden (kWh) und
1 kWh = 3.600 kJ = 3,6 MJ
Beladewärmeleistung ist die Wärmeleistung (Wärme je Zeiteinheit), mit der ein Wärmespeicher beladen wird. Sie wird in kW oder MW angegeben, wobei gilt:
1 Megawatt (MW) = 1.000 Kilowatt (kW)
Entladewärmeleistung wird analog zur Beladewärmeleistung für den Fall der Entladung
definiert.
2.2 Sensible Wärme
Als „sensible Wärme“ wird die Wärmeaufnahme oder -abgabe bezeichnet, die mit einer fühlbaren Änderung der Temperatur verbunden ist. Den Zusammenhang zwischen Wärmemenge
und Temperaturänderung beschreibt die folgende Gleichung (Gleichung 1):
Q = m · cp · (θ2 – θ1)
Sp
Die Wärmemenge ist neben der Temperaturdifferenz von der Stoffmasse m und der spezifischen Wärmekapazität cp des Stoffes abhängig.
Die spezifische Wärmekapazität ist eine physikalische Stoffeigenschaft. Sie wird mit cp
abgekürzt und besitzt die Einheit kJ/kg K.
Die spezifische Wärmekapazität eines Stoffes gibt an, welche Wärmemenge 1 kg des Stoffes zugeführt werden muss, um seine Temperatur um 1 Kelvin zu erhöhen.
Für die Wärmespeicherung sind Stoffe mit einer hohen spezifischen Wärmekapazität von
Vorteil, um jeweils nur eine geringe Menge des Stoffes einzusetzen. Die spezifische Wärmekapazität gebräuchlicher Speichermedien ist begrenzt, wobei Wasser mit 4,19 kJ/kg K einen
der höchsten Werte erreicht. Für einige Stoffe ist die spezifische Wärmekapazität in Abb. 5
zusammengestellt. Da für die Wärmespeicherung oft nicht die Masse, sondern das Volumen
entscheidender ist, sind zusätzlich die Stoffdichte und die volumetrische Wärmekapazität cp'
aufgeführt. Sie gibt an, wie viel Wärme in einem m3 eines Stoffes gespeichert werden kann,
wenn seine Temperatur um 1 Kelvin erhöht wird.
Sand, Kies und Gestein werden vorwiegend in Erdreich-Wärmespeichern genutzt, Beton
bei der Wärmespeicherung in Gebäuden. In Speichern zur Brauchwassererwärmung und in
Heizungsanlagen kommt überwiegend Wasser zum Einsatz. Wärmeträgeröl wird in Solaranlagen mit Parabolrinnenkollektoren als Wärmeträger und auch als Speichermedium einge11
Physikalische Grundlagen der Wärmespeicherung
setzt. Da Wärmeträgeröl teuer und dessen spezifische Wärmekapazität gering ist, werden in
den Speichern Eisenplatten aufgrund ihrer deutlich höheren Wärmekapazität als eigentliches
Speichermedium eingebaut. In Solarturmkraftwerken werden Salzschmelzen als Wärmeträger und/oder als Speichermedium genutzt. Natrium kann ebenfalls in Solarturmkraftwerken
als Wärmeträgermedium und als Speichermedium verwendet werden.
Medium
Temperaturbereich
Spezifische
Wärmekapazität
cp
Volumetrische
Wärmekapazität
cp'
Dichte
ρ
°C
kJ/kg K
kJ/m3 K
kg/m3
Wasser
0–100
4,19
4175
998
Kies, Sand
0–800
0,71
1.278–1.420
1.800–2.000
Granit
0–800
0,75
2.062
2.750
Beton
0–500
0,88
1.672–2.074
1.900–2.300
0–1.000
0,84
1.176–1.596
1.400–1.900
Eisen
0–800
0,47
3.655
7.860
Wärmeträgeröl
0–400
1,6–1,8
1.360–1.620
850–900
Kies-Wasser-Schüttung
(37 Vol.-% Wasser)
0–100
1,32
2.904
2.200
Salzschmelze (53KNO3 +
40NaNO2 + 7NaNO3)
150–450
1,3
1.970–1.725
2.561–2.243
Natrium
100–800
1,3
925–750
1.203–975
Ziegelstein
Abb. 5: Spezifische und volumetrische Wärmekapazität von Wärmespeichermaterialien bei 20 °C
An zwei Beispielen soll die praktische Umsetzung der Ausführungen in diesem Abschnitt
demonstriert werden:
Beispiel: Wie viele m3 Wasser sind notwendig, um zwischen den Temperaturen 40 °C und
90 °C den jährlichen Heizwärmebedarf eines Einfamilienhauses zu speichern, wenn dessen
Heizölverbrauch 1.000 l/a beträgt?
Lösung: Der Heizwert von Heizöl beträgt rund 10 kWh/l. Demnach müssen 10.000 kWh bzw.
36.000 MJ gespeichert werden. Aus Gleichung 1 folgt
m=
12
Q Sp
36.000.000 kJ
=
= 171.838 kg Wasser
c p · (θ2 − θ1 ) 4,19 kJ / kg K · (90 − 40 ) K
Latente Wärme
Zur Speicherung der Wärme im genannten Temperaturbereich sind rund 172 m3 Wasser
erforderlich. Etwaige Wärmeverluste wurden bei dieser überschlägigen Berechnung nicht
berücksichtigt.
Beispiel: Wie viel Wärme lässt sich in einer Hauswand aus Beton mit den Abmessungen
2,3 m · 4 m · 0,2 m speichern, wenn ihre Temperatur um 2 Grad erhöht wird?
Lösung: Das Volumen der Wand beträgt V = 1,84 m3. Mit Hilfe der volumetrischen Wärmekapazität aus Abb. 5 folgt
QSp = V · cp' · (θ2 – θ1) = 1,84 m3 · 1.800 kJ/kg K · 2 K = 6.624 kJ = 1,84 kWh.
Dies entspricht in etwa der Wärmemenge, die in 24 Stunden durch diese Wand bei einer
Außentemperatur von 0 °C und einer Raumtemperatur von 20 °C hindurchgeht, wenn sie mit
100 mm Mineralfaserdämmung isoliert ist.
2.3 Latente Wärme
Als latente Wärme bezeichnet man die bei einem Phasenübergang aufgenommene oder abgegebene Wärmemenge. Sie wird „versteckte Wärme“ oder „latente Wärme“ genannt, da die Aufnahme bzw. Abgabe dieser Wärme zu keiner merklichen Temperaturänderung führt.
Die latente Wärme ist aus dem Alltag bekannt. Sie ist z. B. für die lange Zeitdauer für das
Auftauen von Gefriergut verantwortlich. Zum Schmelzen muss reichlich Wärme zugeführt
werden, was aufgrund des schlechten Wärmeübergangs viel Zeit in Anspruch nimmt. Umgekehrt ist beim Gefrieren (oder präziser beim Erstarren) genau diese Wärme abzuführen. Für
die Wärmespeicherung sind derartige Vorgänge günstig, da die ausgespeicherte Wärme bei
einer konstanten Temperatur zur Verfügung steht. Neben der Umwandlung fest/flüssig ist die
Phasenumwandlung flüssig/gasförmig zu nennen, bei der Wärme ohne Änderung der Temperatur zu- bzw. abgeführt wird. Verdampfen und Kondensieren sind ebenfalls Vorgänge, die aus
dem Alltag bekannt sind. So steigt die Temperatur z. B. beim Kochen von Wasser trotz weiterer Wärmezufuhr lange Zeit nicht über 100 °C an. Das Wasser verdampft, der Dampf nimmt
die Wärme mit und gibt sie beim Kondensieren an kalte Flächen (z. B. Fenster) ab.
Die Temperatur von Eis/Wasser/Wasserdampf ist als Funktion der Enthalpie (bzw. der
gespeicherten Wärme) in Abb. 6 dargestellt. Im festen Zustand (Eis) steigt die Temperatur bei
Wärmezufuhr an, die spezifische Wärmekapazität beträgt 2,1 kJ/kg K. Während des Schmelzvorgangs hingegen bleibt die Temperatur konstant. Die Schmelzwärme beträgt 335 kJ/kg; sie
entspricht etwa der Wärmemenge, die für das Aufheizen der gleichen Menge Wasser von 0
auf 80 Grad erforderlich ist.
Im flüssigen Zustand ändert sich die Temperatur bei Wärmezufuhr langsamer als im festen
Zustand, da die spezifische Wärmekapazität in der flüssigen Phase ungefähr den doppelten
13
Physikalische Grundlagen der Wärmespeicherung
Abb. 6: Temperatur als Funktion
der Enthalpie von Wasser
Wert annimmt. Zur Verdampfung müssen rund 2.250 kJ/kg zugeführt werden, was etwa der
5,4-fachen Energiemenge entspricht, die für das Aufheizen der gleichen Menge Wasser von
0 °C auf 100 °C erforderlich ist. Da sich das Volumen bei der Verdampfung vertausendfacht,
ist diese latente Wärme trotz des hohen Betrags nur bedingt für die Wärmespeicherung nutzbar. Es gibt allerdings Prozesse, bei denen die Verdampfungswärme von Wasser genutzt werden kann (z. B. die Adsorption von Wasserdampf in Silicagel).
Zur Berechnung der Wärme, die in einer Masse m eines Latentspeichermaterials gespeichert wird, muss Gleichung 1 um den Anteil der latenten Wärme erweitert werden, die folgendermaßen definiert ist:
Umwandlungswärme oder latente Wärme ist diejenige Wärme, die 1 kg eines Stoffs zur
vollständigen Änderung seines Aggregatzustandes bei konstanter Temperatur zugeführt werden muss. Sie wird mit ∆hf abgekürzt und besitzt die Einheit kJ/kg, d. h. Wärmemenge je Masseneinheit.
Die Temperatur, bei der die Umwandlung stattfindet, wird mit θf bezeichnet. Berücksichtigt
man ferner, dass das Latentspeichermaterial in einem Temperaturbereich zwischen θ1 und θ2
beide Aggregatzustände (z. B. fest und flüssig) einnehmen kann, ergibt sich Gleichung 2.
QSp = m · [cp,1 · (θf – θ1) + hf + cp,2 · (θ2 – θf )]
Die in einem Latentspeichermaterial zwischen den Temperaturen θ2 und θ1 gespeicherte
Wärme setzt sich aus der sensiblen Wärme unterhalb der Umwandlungstemperatur, der
Umwandlungswärme selbst und der sensiblen Wärme oberhalb der Umwandlungstemperatur zusammen. Bei Latentspeichermaterialien wird der Temperaturbereich θ2 – θ1 klein
gewählt, da das Hauptaugenmerk auf der latenten Wärmespeicherung liegt.
Bisher konzentrieren sich die Anwendungen von Latentspeichermaterialien, die üblicherweise kurz als PCM (engl. Phase Change Material) bezeichnet werden, vor allem auf den Phasenübergang fest–flüssig. Im Bereich der dezentralen, netzunabhängigen Anwendungen zum
14
Latente Wärme
Medium
Wasser
Paraffine
Eicosan
Rohparaffin
Fettsäuren
Laurinsäure
Myristinsäure
Stearinsäure
– rein
– technisch
Umwandlung
Umwandlungstemperatur
θf
Umwandlungswärme
∆hf
Spezifische
Wärmekapazität
cp1/cp2
°C
kJ/kg
kJ/kg K
fest/flüssig
flüssig/gasförmig
0
100
335
2.540
2,1/4,19
4,19/1,86
fest/flüssig
fest/flüssig
36,6
34,3
243
142
1,94/2,08
fest/flüssig
fest/flüssig
fest/flüssig
44
54
183
187
1,8/2,16
69,7
64,8
221
203
1,83/2,3
Salzhydrate
Na2SO4 10H2O
Na2S2O3 5H2O
Ba(OH)2 8H2O
fest/flüssig
fest/flüssig
fest/flüssig
32
48
78
241
201,2
266,7
Salzgemische
48NaCl/52MgCl2
67NaF/33MgF2
fest/flüssig
fest/flüssig
450
832
432
618
0,9/1,0
1,42/1,38
Abb. 7: Umwandlungstemperatur und Umwandlungswärme einiger Latentspeichermaterialien
Warm- oder Kalthalten (z. B. Transportboxen) sind schon heute wirtschaftliche Produkte am
Markt verfügbar. Der Durchbruch als Standardtechnologie im Bereich der Wärme- oder Kältespeicherung hängt neben der Entwicklung von geeigneten Speichermaterialien von der
Lösung konstruktiver Probleme ab:
❏ PCM weisen meist eine schlechte Wärmeleitfähigkeit auf, so dass die Wärmetransportwege im
Speicher im Hinblick auf eine nennenswerte Leistungsentnahme optimiert werden müssen.
❏ PCM ändern ihr Volumen beim Schmelzen und Erstarren. Durch die Bildung von Hohlräumen in der Phase mit dem geringeren Volumen wird der Wärmetransport behindert.
❏ Einige Materialien (z. B. Salzhydrate) sind korrosiv gegen Metalle, so dass teure Speicherbehälter aus Edelstahl erforderlich sind. Andere Materialien sind nicht langzeitstabil. Ihr
Verhalten kann durch Entmischung und durch chemische Veränderungen beeinträchtigt
werden.
Abschließend wird an einem Beispiel gezeigt, wie sich die Volumina von Wasser- und Latentspeichern zueinander verhalten.
Beispiel: Wie viel Stearinsäure ist notwendig, um im Bereich zwischen 60 °C und 80 °C eine Wärmemenge von 100 kWh zu speichern? Wie viel Wasser ist für denselben Zweck erforderlich?
15
Physikalische Grundlagen der Wärmespeicherung
Lösung: Mit Gleichung 2 und den Werten aus Abb. 7 ergibt sich
m=
Q Sp
[c ⋅(θ − θ ) + ∆h + c ⋅(θ − θ )]
p ,1
f
1
f
p ,2
2
=
f
360.000 kJ
1, 8 ⋅ 69, 7 − 60 + 221 + 2, 2 ⋅ 80 − 69, 7
(
)
(
)
m = 1.379 kg
Für die Speicherung von 100 kWh werden etwa 1.379 kg Stearinsäure benötigt, die ein Volumen von rund 1,5 m3 beanspruchen. Nach Gleichung 1 sind ca. 4,3 m3 Wasser bzw. ungefähr
das dreifache Volumen notwendig, um dieselbe Wärmemenge im angegebenen Temperaturbereich zu speichern. Vergrößert man den nutzbaren Temperaturbereich auf das Intervall von
40 °C bis 80 °C, so sind nur noch 2,15 m3 Wasser oder 1,35 m3 Stearinsäure erforderlich.
Aus dem Beispiel wird ersichtlich, dass Latentwärmespeicher den Wasserspeichern nur bei einem
kleinen für die Wärmespeicherung nutzbaren Temperaturbereich deutlich überlegen sind.
2.4 Chemische Wärmespeicherung
Bei der chemischen Wärmespeicherung wird die Reaktionsenergie ausgenutzt. Der große Vorteil liegt in der höheren Energiedichte sowie dem Fehlen von Wärmeverlusten auch bei langer Speicherungsdauer.
Das Prinzip der chemischen Energiespeicherung ist aus der Natur bekannt. Die Vorräte an
Kohle, Erdöl und Erdgas sind verkürzt dargestellt aus Pflanzenresten entstanden und stellen
letztendlich gespeicherte Sonnenenergie dar. Unsere Energieversorgung der letzten 200 Jahre
wird aus diesem großen, aber endlichen Speicher gedeckt. Die Verbrennung der fossilen Energieträger ist nichts anderes als eine chemische Reaktion mit Sauerstoff bei hoher Temperatur,
bei der die Bindungsenergie der chemischen Reaktion in Form von Wärme freigesetzt wird.
Bei fast allen diesen Verbindungen ist Kohlenstoff beteiligt, der zusammen mit Sauerstoff zu
Kohlendioxid reagiert. Der umgekehrte Prozess findet bei der Photosynthese statt, bei dem
aus Kohlendioxid mit Hilfe von Sonnenlicht wieder Sauerstoff und Kohlenstoffverbindungen
entstehen. Prozesse, die für die technische Anwendung momentan untersucht werden, laufen
bei niedrigeren Temperaturen ab (bis ca. 700 °C) und haben eine mehr als zehnmal geringere
Reaktionswärme als die Oxidation von fossilen Brennstoffen.
Die technische Anwendung der chemischen Energiespeicherung ist keineswegs neu. Beckmann und Gilli [1] berichten, dass bereits 1882 eine Lokomotive, die zwischen Aachen und
Jülich verkehrte, ihre Energie aus einem chemischen Speicher bezog, und dass 1883 ein Motorboot auf der Spree auf dieselbe Art angetrieben wurde. Als Speichermedium diente konzentrierte Natronlauge (NaOH), die beim Einleiten von Wasser oder Dampf Wärme entwickelt.
Mit Hilfe dieser Wärme wurde Dampf erzeugt, der die Lokomotive antrieb. Nach verrichteter
16
Chemische Wärmespeicherung
Reaktion
Reaktionstemperatur
Reaktionswärme
°C
kJ/kg
258
479
555
1.473
280–500
druckabhängig
2.885
druckabhängig
467
2.930
Reversible Zersetzung von Ammoniakaten
CaCl2 · 8 NH3 ↔ CaCl2 · 4 NH3 + 4 NH3
90–100
745
Adsorption von Wasser in Silicagel
Silicagel + Dampf ↔ Silicagel feucht
Reversible Wasserabspaltung
CaCl2 · 2 H2O ↔ CaCl2 · H2O + Dampf
Ca(OH)2 ↔ CaO + Dampf
Reversible Zersetzung von Metallhydriden
MgH2 ↔ Mg + H2
Reversible Zersetzung von Salzen
NH4SO4 ↔ NH3 + H2O + SO3
40–100
991
Reversible Zersetzung von Metallkarbonaten
CaCO3 ↔ CaO + CO2
837
1.780
Verdünnung von Schwefelsäure
H2SO4 + xH2O ↔ H2SO4 (verdünnt)
400
816
Zum Vergleich: Verbrennung
CH4 + 2 O2 → CO2 + 2 H2O (Erdgas)
2 H2 + O2 → 2 H2O
je kg CH4
je kg H2
50.144
120.900
Abb. 8: Reaktionspaare für die chemische Wärmespeicherung
Arbeit wurde der Dampf in die Natronlauge eingeleitet und führte dort zu weiterer Wärmeerzeugung. Wenn der Speicher entladen, d. h. die Lauge verdünnt war und keine Wärme mehr
entnommen werden konnte, wurde die Lauge ausgewechselt und in einer stationären Anlage
durch Ausdampfen des Wassers (Wärmezufuhr) wieder regeneriert.
Für die chemische Energiespeicherung werden Reaktionen gesucht, die im technischen
Maßstab umkehrbar (reversibel) sind. Die Vorgänge der Speicherbeladung und -entladung
lassen sich mit den Reaktionsgleichungen 3 und 4 schematisch beschreiben:
A–B
A+B
H
→
A + B (Speicherladung)
– H
→ A – B (Speicherentladung)
Der Term H stellt die Reaktionsenthalpie (oder Reaktionswärme) dar, die bei der Reaktion
umgesetzt wird. Sie wird wie die Umwandlungswärme von Latentspeichermaterialien in der
Einheit kJ/kg gemessen, während in der Chemie üblicherweise die für die Berechnung prak17
Physikalische Grundlagen der Wärmespeicherung
tikablere Einheit kJ/mol für die Angabe der Reaktionsenthalpie genutzt wird. Abb. 8 enthält
beispielhaft einige Stoffpaare und die dazugehörigen Reaktionswärmen, die für die Wärmespeicherung in Frage kommen.
Bei näherer Betrachtung von Abb. 8 fällt auf:
❏ Die Reaktionswärmen sind zum Teil mehr als 10-mal so groß wie bei Latentspeichermaterialien. Dennoch betragen sie weniger als ein Zehntel der Reaktionswärmen der üblichen
Verbrennungsvorgänge mit Sauerstoff.
❏ Die Reaktionstemperaturen liegen meist weit über 100 °C. Für die Speicherung von Sonnenenergie bedeutet dies, dass konzentrierende Systeme (Parabolrinnen bis etwa 400 °C, darüber Solarturmkraftwerke) zur Sammlung der Sonnenenergie verwendet werden müssen.
❏ Einer der Reaktionspartner ist im Zustand höherer Energie (beladener Speicher) gasförmig und benötigt ein entsprechend großes Volumen zur Speicherung.
Der große Vorteil chemischer Energiespeicherung liegt darin, dass die Reaktionspartner bei
Umgebungstemperatur beliebig lange gelagert werden können, ohne dass Wärmeverluste zu
verzeichnen sind.
Nicht nur die Reaktionswärme, sondern auch die Reaktionspartner selbst lassen interessante Anwendungen zu. Das Gas NH3 (Ammoniak) kann zur Kälteerzeugung verwendet werden, Wasserstoff kann zum Antrieb von Maschinen und Fahrzeugen dienen.
2.5 Wärmeverluste von Wärmespeichern
Speicher für sensible und latente Wärme weisen aufgrund der vorhandenen Temperaturdifferenz zwischen Speichermaterial und Umgebungstemperatur unvermeidbare Wärmeverluste
an die Umgebung auf. Bevor an einigen Beispielen die Größe der Wärmeverluste veranschaulicht wird, sollen zunächst die physikalischen Grundlagen erläutert werden.
Zur Verminderung von Wärmeverlusten werden Speicher mit Wärmedämmmaterialien
isoliert. Der Wärmestrom durch die Wärmedämmung lässt sich mit Hilfe von Gleichung 5
beschreiben.
v = U · A · (θSp – θa)
Die Wärmeverluste hängen von der Oberfläche des Speichers A, der Temperaturdifferenz zwischen Speicher und Umgebung und dem Wärmedurchgangskoeffizient U ab. Der Koeffizient U
wiederum ist von der Dicke des Dämmmaterials s und von seiner Wärmeleitfähigkeit λ abhängig, wie Gleichung 6 zu entnehmen ist. Die Wärmeübergangswiderstände auf der Innen- und
Außenseite werden vernachlässigt, da der Wärmedurchgangskoeffizient in der Regel fast ausschließlich von der Dämmwirkung bestimmt wird. Der Koeffizient U gibt an, wie groß der
Wärmestrom pro m2 und Kelvin durch die Wärmedämmung ist.
18
Wärmeverluste von Wärmespeichern
U = λ/s
Die Wärmeleitfähigkeit der meisten für die Speicherisolierung eingesetzten Wärmedämmstoffe liegt bei etwa 0,04 W/m2 K.
Beispiel: Wie groß ist der Wärmestrom durch die Wärmedämmung eines zylindrischen Trinkwarmwasserspeichers mit einem Volumen von 500 l und einem Durchmesser von 0,6 m, der
mit einer 10 cm dicken Wärmedämmung versehen ist? Die Speichertemperatur beträgt 50 °C,
die Umgebungstemperatur 10 °C. Wie viel Wärme verliert der Speicher während eines Jahres?
Lösung: Mit Hilfe von Gleichung 6 ergibt sich ein U-Wert von 0,4 W/m2 K. Die Höhe des Speichers beträgt 1,77 m, seine Oberfläche 3,9 m2. Die äußere Oberfläche inklusive der Wärmedämmung erreicht 5,96 m2. Als Bezugsfläche für den Wärmeverlust wird der Mittelwert dieser beiden Flächen mit A = 4,93 m2 angesetzt. Daraus ergibt sich nach Gleichung 5 ein Wärmestrom von
2
2
v = 0,4 W/m K · 4,93 m · (50 – 10) K = 78,9 W.
Den Gesamtverlust über ein Jahr erhält man durch Multiplikation mit der Zeitdauer
v = 78,9 W · 8760 h/a = 690,7 kWh/a.
Die berechnete Wärmemenge entspricht etwa dem Heizwert von 70 m3 Erdgas oder 70 l Heizöl.
Vergleicht man die Wärmeverluste mit der Wärmemenge, die für die Aufheizung des Wassers
notwendig ist (bei 500 l/d und einer Kaltwassertemperatur von 10 °C sind dies 23,2 kWh/d
bzw. 8.470 kWh/a), betragen die Wärmeverluste etwa 8 % dieser Wärmemenge.
In der Realität weist ein Warmwasserspeicher dieser Größenordnung deutlich höhere Wärmeverluste auf, da über Wärmebrücken sowie die angeschlossenen Rohrleitungen zusätzlich
Wärme aus dem Speicher verloren geht. Kritische Stellen für Mängel in der Wärmedämmung
sind häufig Flansche und Anschlüsse. Eine erhebliche Verlustquelle stellen oben aus dem Speicher herausgeführte Anschlussleitungen für warmes Wasser dar. Aufgrund der Dichteunterschiede zwischen heißem Speicherwasser und sich in der Rohrleitung abkühlendem Wasser
stellen sich in der Rohrleitung zirkulierende Strömungen ein, die das heiße Wasser aus dem
Speicher in die Rohrleitung transportieren und das dort abgekühlte wieder in den Speicher
zurückfließen lassen.
Allein die Wärmeverluste über eine solche Rohrleitung können die Wärmeverluste des Speichers um etwa 50 % erhöhen. Bei modernen Solarspeichern (s. Abb. 9) sind die Anschlüsse
für die Wärmeübertrager, Kalt- und Warmwasseranschluss, aus diesem Grund unten angeordnet. Das heiße Wasser wird in der Regel über ein Kunststoffrohr aus dem oberen Speicher19
Physikalische Grundlagen der Wärmespeicherung
Abb. 9: Solarspeicher
bereich entnommen (vgl. dazu auch Kap. 4). Diese Konstruktion erlaubt es, die Wärmedämmung ohne jedweden Durchbruch über den Speicher zu ziehen. Wärmeverluste über oben
angeschlossene Rohrleitungen werden vermieden.
Ein weiteres Beispiel demonstriert das Problem der Wärmeverluste bei Langzeit-Wärmespeichern. In Kapitel 2.2 wurde berechnet, dass zur Speicherung des jährlichen Heizenergiebedarfs eines Hauses ohne Berücksichtigung der Wärmeverluste ein Wasservolumen von 172 m3
erforderlich ist. An dieser Stelle sollen die Wärmeverluste überschlägig abgeschätzt werden.
Beispiel: Wie groß sind die Wärmeverluste eines Langzeit-Wärmespeichers mit einem Volumen von 172 m3? Die Dicke der Wärmedämmung beträgt allseitig 0,5 m, der Speicher hat die
Form eines Würfels mit der Kantenlänge 5,56 m, die mittlere Temperatur wird mit 70 °C angenommen, die mittlere Umgebungstemperatur mit 15 °C.
Lösung: Die Oberfläche des Speichers ohne Wärmedämmung beträgt 185 m2, mit Isolierung
258 m2, die mittlere Fläche 222 m2. Den Wärmedurchgangskoeffizienten U berechnet man
mit Gleichung 6 zu 0,08 W/m2 K, über Gleichung 5 den Wärmestrom zu 0,98 kW. Durch Multiplikation mit der Zeitdauer ergibt sich ein jährlicher Wärmeverlust von rund 8.600 kWh. Im
Beispiel in Kapitel 2.2 sollten 10.000 kWh gespeichert werden. Da zusätzlich 8.600 kWh Wärmeverluste gedeckt werden müssen, muss der Speicher nahezu doppelt so groß sein, um im
Winter die gewünschte Wärmemenge entnehmen zu können.
Das Beispiel zeigt deutlich, dass die Speicherung von fühlbarer Wärme im Maßstab des
Wärmebedarfs von Einzelhäusern nicht sinnvoll ist. Selbst bei sehr dicker Wärmedämmung
20
Wärmeverluste [%]
Wärmeverluste von Wärmespeichern
Abb. 10: Anteil der Wärmeverluste
an der gespeicherten Wärmemenge über ein Jahr als
Funktion des Speichervolumens (Speicher würfelförmig)
50
Temperaturbereich
90/40 °C
Mittlere Temperatur
70 °C
Umgebungstemperatur
15 °C
Wärmedämmung
0,5 m
Speichermedium Wasser
40
30
20
10
0
0
20
40
60
80
100
120
140
160
180
200
Speichervolumen [1.000 m3]
sind die Wärmeverluste zu groß. Fasst man den Speicher von 100 Häusern zu einem gemeinsamen Speicher zusammen, ergibt sich ein Speichervolumen von 17.200 m3. Die Wärmeverluste erreichen jedoch nur ungefähr das 10fache des kleinen Speichers. Sie können von etwa
77 % auf rund 16 % reduziert werden. Abb. 10 zeigt für das betrachtete Beispiel die Abnahme
der Speicherwärmeverluste bei zunehmender Speichergröße anschaulich. Es wurde jedoch
nur eine grobe Abschätzung vorgenommen. Temperaturverlauf sowie Temperaturschichtung innerhalb des Langzeit-Wärmespeichers wurden außer Acht gelassen (vgl. dazu auch
Kap. 7).
Aus diesen Beispielen wird zweierlei deutlich:
❏ Langzeit-Wärmespeicherung fühlbarer Wärme kann nur in großen Wärmespeichern stattfinden, da nur hier die Wärmeverluste auf vertretbare Größenordnungen reduziert werden
können;
❏ die große Bedeutung chemischer Speicher für die Langzeit-Wärmespeicherung, da Wärme
ohne Verluste gespeichert werden kann.
21