Papierproduzent (2) (B)

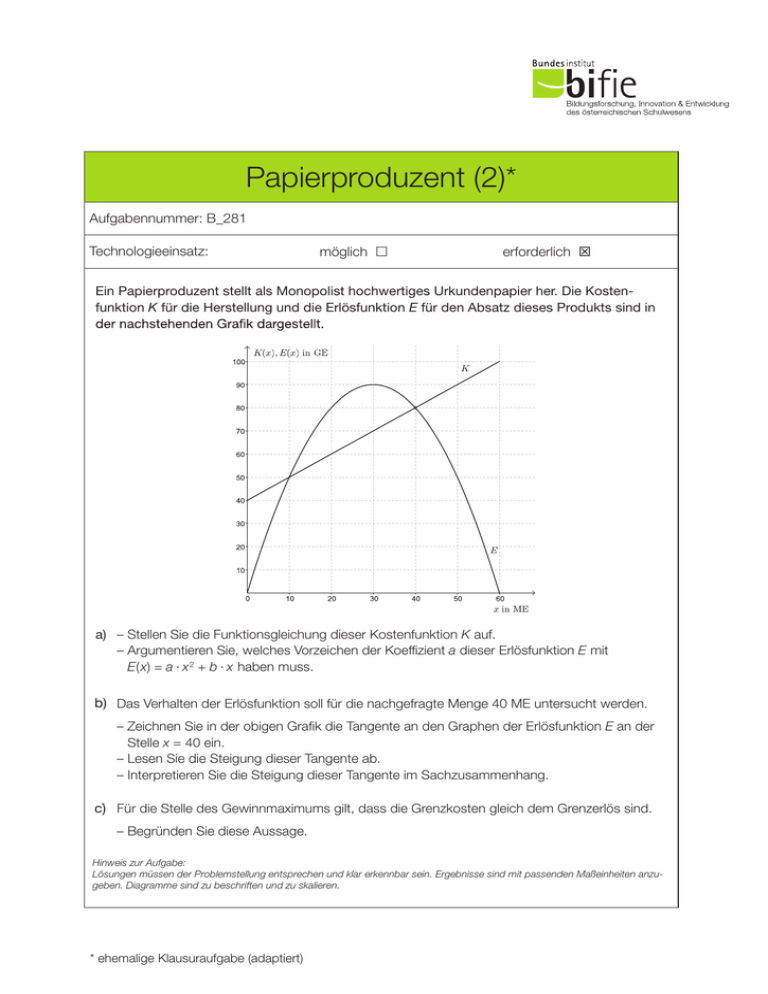
Aufgabe 8
Papierproduzent
Ein Papierproduzent stellt als Monopolist hochwertiges Urkundenpapier her. Die Kostenfunktion K für die Herstellung und die Erlösfunktion E für den Absatz dieses Produkts sind in
Aufgabe 8
Papierproduzent (2)*
Aufgabennummer: B_281
Technologieeinsatz:
Papierproduzent
möglich £
erforderlich T
Ein Papierproduzent stellt als Monopolist hochwertiges Urkundenpapier her. Die Kostenfunktion K für die Herstellung und die Erlösfunktion E für den Absatz dieses Produkts sind in
a) – Stellen Sie die Funktionsgleichung dieser Kostenfunktion K auf.
– Argumentieren Sie, welches Vorzeichen der Koeffizient a dieser Erlösfunktion E mit
E(x) = a · x 2 + b · x haben muss.
b) Der Zusammenhang zwischen dem Preis und der nachgefragten Menge lässt sich durch folgende Preisfunktion der Nachfrage pN beschreiben:
pN(x) = –0,1 · x + 6
x ... Anzahl der nachgefragten Mengeneinheiten (ME)
pN(x) ... Preis in Geldeinheiten pro Mengeneinheit (GE/ME) bei der Nachfrage von x ME
Der Papierproduzent überlegt, den Preis von 5 GE/ME auf 4 GE/ME zu senken. Die Kostenrechnungsabteilung behauptet: „Die Bogenelastizität der Nachfrage für diese Preissenkung
a) –beträgt
Stellen–5.“
Sie die Funktionsgleichung dieser Kostenfunktion K auf.
–– Argumentieren
welchesdie
Vorzeichen
derdieser
Koeffizient
a dieser Erlösfunktion E mit
Überprüfen Sie Sie,
rechnerisch
Richtigkeit
Behauptung.
2
= aSie
· x eine
+ b Funktionsgleichung
· x haben muss.
– E(x)
Stellen
für die Punktelastizität der Nachfrage auf.
b)
zwischen dem
Preis
der nachgefragten
Menge
lässt sich werden.
durch folb)
c) Der
Das Zusammenhang
Verhalten der Erlösfunktion
soll für
dieund
nachgefragte
Menge 40
ME untersucht
gende Preisfunktion der Nachfrage pN beschreiben:
– Zeichnen Sie in der obigen Grafik die Tangente an den Graphen der Erlösfunktion E an der
pNStelle
(x) = –0,1
· x ein.
+6
x = 40
Lesen
Sieder
die nachgefragten
Steigung dieserMengeneinheiten
Tangente ab. (ME)
x– ...
Anzahl
– Interpretieren
die Steigung
Tangente im
Sachzusammenhang.
p
(x) ... Preis in Sie
Geldeinheiten
prodieser
Mengeneinheit
(GE/ME)
bei der Nachfrage von x ME
N
6
Der die
Papierproduzent
überlegt, den Preis
GE/ME
auf 4 GE/ME
senken.
Die Kostend) Für
Stelle des Gewinnmaximums
gilt, von
dass5 die
Grenzkosten
gleichzudem
Grenzerlös
sind.
c)
öffentlichesrechnungsabteilung
Dokument
behauptet: „Die Bogenelastizität der Nachfrage für diese Preissenkung
–beträgt
Begründen
–5.“ Sie diese Aussage.
– Überprüfen
Hinweis
zur Aufgabe: Sie rechnerisch die Richtigkeit dieser Behauptung.
Lösungen
müssenSie
der eine
Problemstellung
entsprechen und
erkennbar
sein. Ergebnisse
mit passenden
– Stellen
Funktionsgleichung
fürklardie
Punktelastizität
dersind
Nachfrage
auf.Maßeinheiten anzugeben. Diagramme sind zu beschriften und zu skalieren.
c) Das Verhalten der Erlösfunktion soll für die nachgefragte Menge 40 ME untersucht werden.
– Zeichnen Sie in der obigen Grafik die Tangente an den Graphen der Erlösfunktion E an der
Stelle x = 40 ein.
* ehemalige Klausuraufgabe (adaptiert)
– Lesen Sie die Steigung dieser Tangente ab.
– Interpretieren Sie die Steigung dieser Tangente im Sachzusammenhang.
Papierproduzent
Möglicher Lösungsweg
Papierproduzent
(2)
2
a) Kostenfunktion: K(x) = x + 40
Aufgabe 8 (Teil B)
Erlösfunktion: Der Koeffizient a muss negativ sein, weil der Funktionsgraph der Erlösfunktion
eine nach unten geöffnete Parabel ist.
Papierproduzent
b) 5 = –0,1 ∙ x + 6 ⇒ x = 10
4 = –0,1 ∙ x + 6 ⇒ x = 20
Möglicher Lösungsweg
∆p
∆x 10
Eine Preissenkung um
= – 1 = –20 % führt zu einer Absatzsteigerung um
=
= 100 %.
p
x
5
10
a) Kostenfunktion: K(x) = x + 40
Die Bogenelastizität der Nachfrage beträgt also tatsächlich: 100 % = –5.
–20 %
Erlösfunktion: Der Koeffizient a muss negativ sein, weil der Funktionsgraph der Erlösfunktion
–0,1 ∙ x + 6
pN(x)
60
eine
nach untender
geöffnete
Parabel
Punktelastizität
Nachfrage:
ε(x) ist.
=
=
=1–
x
x ∙ (–0,1)
x ∙ pN′ (x)
Möglicher Lösungsweg
c) 5 = –0,1 ∙ x + 6 ⇒ x = 10
b)
4 = –0,1 ∙ x + 6 ⇒ x = 20
∆p
∆x 10
Eine Preissenkung um
= – 1 = –20 % führt zu einer Absatzsteigerung um
=
= 100 %.
p
x
5
10
Die Bogenelastizität der Nachfrage beträgt also tatsächlich: 100 % = –5.
–20 %
Punktelastizität der Nachfrage: ε(x) =
–0,1 ∙ x + 6
pN(x)
60
=
=1–
x
x ∙ (–0,1)
x ∙ pN′ (x)
c)
Steigung der Tangente: k = –2
Toleranzbereich: [–2,5; –1,5]
Wird die Absatzmenge um 1 ME erhöht, sinkt der Erlös näherungsweise um 2 GE.
c)
d) G(x) = E(x) – K(x)
An der Stelle des Gewinnmaximums gilt: G′(x) = 0.
G′(x) = 0 = E′(x) – K′(x)
Also: E′(x) = K′(x).
Steigung der Tangente: k = –2
Toleranzbereich: [–2,5; –1,5]
Wird die Absatzmenge um 1 ME erhöht, sinkt der Erlös näherungsweise um 2 GE.
d) G(x) = E(x) – K(x)
öffentliches Dokument
An der Stelle des Gewinnmaximums gilt: G′(x) = 0.
G′(x) = 0 = E′(x) – K′(x)
Also: E′(x) = K′(x).
12
12
öffentliches Dokument
Papierproduzent (2)
3
Lösungsschlüssel
a) 1 × A: für das richtige Aufstellen der Funktionsgleichung
1 × D: für die richtige Argumentation zum Vorzeichen des Koeffizienten a
b) 1 × A: für das richtige Einzeichnen der Tangente
1 × C1: für das richtige Ablesen der Steigung der Tangente im Toleranzbereich [–2,5; –1,5]
1 × C2: für die richtige Interpretation der Steigung der Tangente im Sachzusammenhang
c) 1 × D: für die richtige Begründung