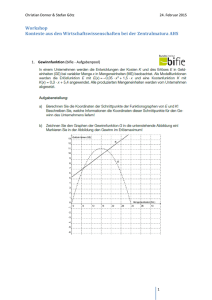
Modellschularbeit Mathematik
Werbung
Kontexte aus den Wirtschaftswissenschaften bei der Zentralmatura AHS http://de.disney.wikia.com/wiki/Datei:Dagobert-duck.jpg Christian Dorner & Stefan Götz Fakultät für Mathematik Bundesseminar Amstetten: 24. Februar 2015 https://www.bifie.at/system/files/dl/srdp_ma_konzept_2013-03-11.pdf Februar 2015 Kleine Dorner Zeitung online vom 18.12.2014 & Götz: Wirtschaftswissenschaften 2 Was sind Typ-2-Aufgaben? Typ-2-Aufgaben sind Aufgaben zur Anwendung und Vernetzung der Grundkompetenzen in definierten Kontexten und Anwendungsbereichen. Dabei handelt es sich um umfangreichere kontextbezogene oder auch innermathematische Aufgabenstellungen, im Rahmen derer unterschiedliche Fragestellungen bearbeitet werden müssen und bei deren Lösung operativen Fertigkeiten gegebenenfalls größere Bedeutung zukommt. Eine selbstständige Anwendung von Wissen und Fertigkeiten ist erforderlich. (Die standardisierte schriftliche Reifeprüfung in Mathematik, S. 23, Hervorhebungen C. D. & S. G.) Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 3 Kontexte bei Typ-2-Aufgaben „Die nachfolgend angeführten Kontexte können jedenfalls ohne detaillierte Erklärung bei der standardisierten Reifeprüfung vorkommen.“ (Die standardisierte schriftliche Reifeprüfung in Mathematik, S. 19, Hervorhebungen C. D. & S. G.) Finanzmathematische Grundlagen: • Zinseszinsrechnung: πΎπ = πΎ0 β 1 + π π mit π = π 100 • Kosten-Preis-Theorie: Erlös(-funktion) Grenzerlös Kosten(-funktion) Grenzkosten Gewinn(-funktion) Grenzgewinn Nachfragepreis(-funktion) Break-even-Point (Die standardisierte schriftliche Reifeprüfung in Mathematik, S. 21 f.) Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 4 Kosten-Preis-Theorie • Erlös- oder Ertragsfunktion … in der Form einer linearen Darstellung: πΈ = π β π₯ mit π … Preis pro Stück und π₯ … Menge der verkauften Ware • Kostenfunktion … in Form einer proportionalen, degressiven, progressiven, regressiven und fixen Darstellung: πΎ π₯ = πΎπ + πΎπ£ (π₯), wobei πΎπ die Fixkosten und πΎπ£ die variablen Kosten sind • Gewinn(-funktion) … als Erlös – Kosten πΊ =πΈ−πΎ • Nachfragepreis(-funktion) … lineare Funktion π = π(π₯) oder π₯ = π₯(π) Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 5 Erlösfunktion oder Ertragsfunktion Achtung: p = p(x) kann passieren!!! Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 6 Kostenfunktion linear Kostenfunktionen sind immer (streng) monoton steigend! Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 7 Kostenfunktion degressiv Mit steigender Produktion werden die Kosten pro Stück geringer! Steigung wird geringer – Krümmung ist negativ Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 8 Kostenfunktion mit Kostenkehre Kostenkehre Wendepunkt Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 9 Modellschularbeit Mathematik (AHS) – Dezember 2014: Aufgabe 6 Achtung: Kontexte auch bei Typ-I-Aufgaben möglich! https://www.bifie.at/node/2744 Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 10 Gewinnfunktion Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 11 Nachfragepreisfunktion Geringer Preis ο große Nachfrage ο große Produktionsmenge Hoher Preis ο geringe Nachfrage ο geringe Produktionsmenge Nachfragepreisfunktion ist immer streng monoton fallend. Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 12 Weitere Begrifflichkeiten: • Break-even-Point: Nullstellen der Gewinnfunktion πΊ =πΈ−πΎ • Grenzkosten: Es handelt sich hierbei um Kosten, die entstehen, wenn von einem Produkt eine Einheit mehr produziert wird. Das ist also die erste Ableitung πΎ ′ der Kostenfunktion. • Grenzerlös πΈ′: analog zu den Grenzkosten πΎ ′ • Grenzgewinn πΊ′: analog zu den Grenzkosten πΎ ′ Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 13 Break-even-Point ο „Die Schnittpunkte der Graphen von Kosten- und Erlösfunktion an den Gewinngrenzen heißen Break-even-Punkte (BEP).“ (S. 69) Malle Götz ο „Als Gewinnschwellen (BEP … Break Even Point) bezeichnet man die Nullstellen der Gewinnfunktion G = E - K; …“ (S. 230) Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 14 Haupttermin 2013/14: Typ-2-Aufgabe „Grenzkosten“ https://www.bifie.at/node/2633 Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 15 Ein Beispiel: Ein Unternehmen arbeitet mit Kosten πΎ π₯ = 0,1π₯ 2 + 0,1x + 2 und dem Preis-Absatz-Zusammenhang 10π + 2,8π₯ = 32, dabei ist π₯ die Absatzmenge und π der (Stück-)Preis: π₯ in Mengeneinheiten ME, π in Geldeinheiten GE Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 16 (1) Gewinn- und Verlustbereich Ges.: die Nullstellen der Gewinnfunktion πΊ = πΈ − πΎ, dazu: 32 − 2,8π₯ πΈ =πβπ₯ = β π₯ = 3,2π₯ − 0,28π₯ 2 = πΈ π₯ 10 ist die Erlös- oder Umsatzfunktion (nicht mehr linear!)→ πΊ(π₯) = 3,2π₯ − 0,28π₯ 2 − 0,1π₯ 2 − 0,1π₯ − 2 = −0,38π₯ 2 + 3,1π₯ − 2: πΊ π₯ = 0 ↔ 0,38π₯ 2 − 3,1π₯ + 2 = 0 π₯1 = 0,7 und π₯2 = 7,45 → Gewinnbereich π, π; π, ππ ME → Verlustbereich β\ π, π; π, ππ ME Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 17 (2) Maximaler Gewinn bei welcher Absatzmenge zu welchem Preis? Dazu: Grenzgewinn πΊ ′ π₯ = −0,76π₯ + 3,1 gleich Null setzen: 0,76π₯ = 3,1 → π₯ = π, π ME und daraus πΊ 4,1 = π, ππ GE und π = Februar 2015 1 10 32 − 2,8 β 4,1 = π, ππ GE Dorner & Götz: Wirtschaftswissenschaften 18 (3) Bedeutet maximaler Gewinn auch maximalen Umsatz? Wie groß ist der Gewinn bei maximalem Erlös? Grenzerlös πΈ ′ π₯ = 3,2 − 0,56π₯ gleich Null setzen: 3,2 3,2 = 0,56π₯ → π₯ = = π, π ME 0,56 → NEIN! πΊ 5,7 = π, ππ GE Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 19 (4) Welche Bedeutung haben die Nullstellen der Erlösfunktion? • πΈ π₯ = π(π₯) β π₯ und • π(π₯) ist eine lineare Funktion von x, π₯ π ist die Umkehrfunktion. ππ = π ME: π1 = π(0) = 3,2 GE, der sogenannte Prohibitivpreis: Das ist der höchstmögliche Stückpreis für dieses Gut. Für höhere Preise besteht keine Nachfrage mehr. Februar 2015 π, π = ππ, ππ ME π, ππ bedeutet π2 = 0 GE, das heißt π₯2 ist die sogenannte Sättigungsmenge, die größtmögliche Verkaufsmenge. ππ = π(π) = Dorner & Götz: Wirtschaftswissenschaften 20 Exkurs - nochmals Haupttermin 2013/14: „Grenzkosten“ Nicht im Kontextkatalog erwähnte Begriffe müssen in der Aufgabenstellung erklärt werden! https://www.bifie.at/node/2633 Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 21 (5) Stückkostenfunktion k 2 π π₯ = 0,1π₯ + 0,1 + π₯ π ′ π₯ = 0,1 − 2 π₯2 und Nullsetzen liefert 0,1= 2 π₯2 bzw. π₯ 2 = 20, was π₯πππ‘ = π, ππ ME zur Folge hat. Die Herstellungsmenge π₯πππ‘ , bei der mit geringsten Stückkosten produziert wird, heißt Betriebsoptimum. Der kleinstmögliche Preis, mit dem gerade noch kostendeckend produziert werden kann, ist dann also π π₯πππ‘ . Februar 2015 Dorner & Götz: Wirtschaftswissenschaften π π₯πππ‘ = π, ππ GE 22 Quelle: Götz, S. und Reichel, H-C.: Mathematik 8 von R. Müller und G. Hanisch. Unter Mitarbeit von C. Wenzel. Mit einer online-Ergänzung von H.-S. Siller und R. Müller. öbv, Wien 2013. Kapitel III.3 Anwendungen von Analysis auf Fragestellungen in der Wirtschaft, S. 229 – 232: Aufgabe 979. Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 23 Spiralprinzip Kosten-Preis-Theorie 8. Klasse: Rekonstruktion der Kostenfunktion aus den Grenzkosten 7. Klasse: • Diskussion von Polynomfunktionen im wirtschaftsmathematischen Kontext • Optimierung (Extremwertaufgaben) 5. Klasse: einfache Modelle mit linearen Funktionen Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 24 5. Klasse: einfache Modelle mit linearen Funktionen Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 25 5. Klasse: einfache Modelle mit linearen Funktionen Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 26 8. Klasse: Rekonstruktion der Kostenfunktion Malle, G., Woschitz, H., Koth, M. u. Salzger, B.: Mathematik verstehen 8. öbv, Wien 2012. Kapitel 4 Anwendungen in der Wirtschaft, S. 62 – 75. Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 27 Spiralprinzip Zinseszinsrechnung 8. Klasse: Dynamische Systeme (Tilgungsplan) 6. Klasse: • geometrische Folgen und Reihen • stetige Verzinsung 3. Klasse: • lineare Verzinsung • Zinseszinsen Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 28 8. Klasse: Dynamische Systeme (Tilgungsplan) Götz, S. und Reichel, H-C.: Mathematik 8 von R. Müller und G. Hanisch. Unter Mitarbeit von C. Wenzel. Mit einer online-Ergänzung von H.-S. Siller und R. Müller. öbv, Wien 2013. Kapitel 1.1 Differenzengleichung erster Ordnung mit einer Variablen, S. 8 – 17: Aufgabe 40. Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 29 ππ+π = ππ β π, ππ − ππππππ, ππ = πππππππ Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 30 Reflexion ο Kennen der einschlägigen Begriffe und ihrer (jeweiligen) Bedeutungen ο Wiedererkennen im Kontext und verständiges Anwenden ο Wissen um Zusammenhänge ο Interpretieren der Ergebnisse im Kontext http://musenblaetter.de/artikel.php?aid=9128 Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 31 „Die Bibel“ Die standardisierte schriftliche Reifeprüfung in Mathematik. Inhaltliche und organisatorische Grundlagen zur Sicherung mathematischer Grundkompetenzen. (Stand: März 2013). Projektteam: V. Aue, M. Frebort, M. Hohenwarter, M. Liebscher, E. Sattlberger, I. Schirmer, H.-S. Siller (Leitung), G. Vormayr, M. Weiß, E. Willau. https://www.bifie.at/node/1442 Februar 2015 Dorner & Götz: Wirtschaftswissenschaften 32
