Das ursprüngliche, durch freie Ladungen erzeugte Feld bezeichnet

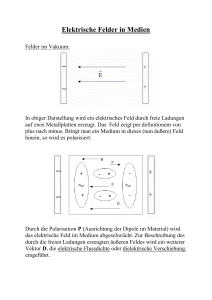
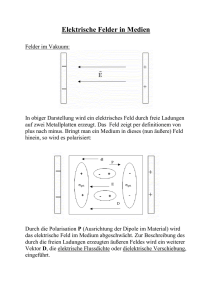
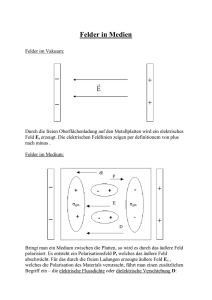
Elektrisches Feld und dielektrische Verschiebung
Das ursprüngliche, durch freie Ladungen erzeugte Feld bezeichnet
man als
dielektrische Verschiebung oder
elektrische Flussdichte
r
D
r
Dabei gilt folgende Beziehung zwischen dem elektrischen Feld E
r
und der dielektrischen Verschiebung D :
r r r
ε0E = D − P
r
Das resultierende elektrische Feld E ergibt sich als Superposition
r
aus dem äußeren Feld und dem Polarisationsfeld P .
Üblicherweise schreibt man:
r
r r
D = ε0E + P
Für die Maßeinheiten gilt:
As
[ε 0 ] =
Vm
r
V
[E] =
m
r
As
[ D] = 2
m
r
As
[P] = 2
m
Aus der Dimension von D und P (Ladung pro Flächeneinheit) ergibt
sich die Bedeutung einer Flächenladungsdichte. Tatsächlich entspricht
den Normalkomponenten von D und P die Oberflächenladungsdichte σ für freie bzw. gebundene Ladungen.
Dn ≡ σfrei
Pn ≡ σgeb.
Durch Einführung der Dielektrizitätszahl εr eliminiert man aus dem
Ausdruck
r
r r
D = ε0E + P
r
die Polarisation P mittels
r
r
D = ε0ε r E
bzw.
r
r
r
P = ε 0 [ ε r − 1]E = ε 0 χ E
χ - dielektrische Suszeptibilität
εr - dielektrische Permeabilität
An der Grenzfläche zweier Medien 1 und 2 mit den Permeabilitäten ε1
und ε2 gelten folgende Bedingungen für die Feldstärken:
Die Normalkomponente Dn der elektrischen Flussdichte ist stetig, d.h.
D n1 = D n 2 = σfrei
Daraus folgt mit
r
r
D = ε0ε r E
r
D 1n = ε 0 ε r1 E n 1 = ε 0 ε r 2 E n 2 = D n 2
das Brechungsgesetz für die Normalkomponente der elektrischen
Feldstärke:
ε r1 E n1 = ε r 2 E n 2
Die Tangentialkomponente der elektrischen Feldstärke ist stetig, d.h.
E t1 = E t 2
Die Größe
r r
Ψ = ∫ D dA
s
bezeichnet man als elektrischen Fluss. Er hat die Dimension einer Ladung.