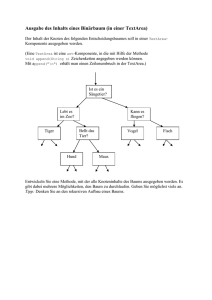
schriftliche Aufgaben - Westsächsische Hochschule Zwickau

Westsächsische Hochschule Zwickau, Fachgruppe Informatik
Prof. S. Schwarz
[email protected]
2.Übung zur Vorlesung Deklarative Programmierung“
”
Wintersemester 2010/2011
gestellt am 19. Oktober 2010
Wiederholung:
• Aufgabe 1.2.c (Binär- zu Dezimaldarstellung)
• Aufgabe 1.4 (strukturelle Induktion auf Peano-Zahlen)
Aufgabe 2.1 (Funktionen auf Listen)
Definieren Sie die folgenden Funktionen (einschließlich Typdeklaration)
a. rev, welche jede gegebene Liste l auf eine Liste der Elemente von l in umgekehrter
Reihenfolge abbildet.
b. palindrom, welche angibt, ob eine eingegebene Zeichenkette ein Palindrom ist.
c. element, welche angibt, ob ein gegebenes Element in einer Liste vorkommt.
d. concat_all, welche alle Zeichenketten in einer gegebenen Liste von Zeichenketten
miteinander verkettet.
e. suffix, welche jede Zeichenkette s auf eine Liste aller Suffixe von s abbildet.
f. praefix, welche jede Zeichenkette s auf eine Liste aller Präfixe von s abbildet.
Aufgabe 2.2 (Induktion auf Listen)
a. Zeigen Sie durch schrittweises Ableiten (Papier), dass gilt:
append [1,4] (append [2] [3,5]) = append (append [1,4] [2]) [3,5]
b. Zeigen Sie, dass für alle Listen xs gilt append xs [] = xs.
c. Zeigen Sie, dass append assoziativ ist, d.h. für alle Listen xs, ys, zs gilt:
append xs (append ys zs) = append (append xs ys) zs
d. Zeigen Sie, dass für Ihre oben entworfene Funktion rev und jede Liste xs gilt:
rev (rev xs) = xs
Aufgabe 2.3 (Funktionen auf Bäumen)
Definieren Sie Funktionen zum
a. Bestimmen der Liste aller Blätter eines binären Baumes
b. Bestimmen der Summe aller Knoten eines binären Baumes (Schlüsseltyp: ganze
Zahlen)
c. Preorder-Duchlauf aller Knoten eines binären Baumes
Aufgabe 2.4 (Induktion auf Bäumen)
Zeigen Sie, das Ihre in der vorigen Aufgabe definierte Funktion zum Einfügen in einen
binären Suchbaum die Suchbaum-Eigenschaft erhält.
Übungsaufgaben, Folien und weitere Hinweise zur Vorlesung finden Sie online unter
http://wwwstud.fh-zwickau.de/~sibsc/lehre/ws10/decprog/.