Serie 5 - HTWK Leipzig

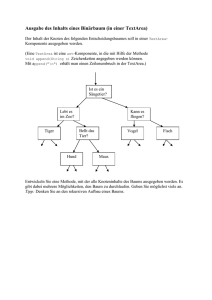
HTWK Leipzig, Fakultät IMN
Prof. Dr. Sibylle Schwarz
[email protected]
5. Praktikum zur Vorlesung Deklarative Programmierung“
”
Sommersemester 2015
gestellt am 18. Mai 2015
Autotool: https://autotool.imn.htwk-leipzig.de/shib/cgi-bin/Super.cgi
Aufgabe 5.1 (Funktionen auf Listen)
Definieren Sie die folgenden Funktionen (Typdeklarationen nicht vergessen):
a. für Int-Listen:
(a) list_prod, welche jede eingegebene Liste von Zahlen auf das Produkt aller
Zahlen in der Liste abbildet.
(b) squares, welche jede eingegebene Liste von Zahlen auf die Liste aller Quadrate der Elemente der Eingabeliste abbildet
(c) square_sum, welche jede eingegebene Liste von Zahlen auf die Summe aller
Quadrate der Elemente der Eingabeliste abbildet
(d) list_min, welche jede eingegebene Liste von Zahlen auf die kleinste in der
Liste vorkommende Zahl abbildet,
(e) all_equal, welche feststellt, ob eine Liste nur gleiche Elemente enthält.
b. für Listen über beliebigem Typ:
(a) n_mal, welche eine eingegebene Liste vervielfacht,
Eingabe: n ∈ , Liste s
Ausgabe: |s ◦ ·{z
· · ◦ s} (mit Verkettung ◦)
N
n−mal
(b) alle_zweimal, welche jedes Element der Ursprungsliste zweimal nacheinander enthält.
(z.B. alle_zweimal [ "foo", "bar" ] = [ "foo", "foo", "bar", "bar"] )
(c) rev, welche jede gegebene Liste xs :: [a] auf die Liste der Elemente von
xs in umgekehrter Reihenfolge abbildet.
(d) palindrom, welche angibt, ob eine eingegebene Zeichenkette ein Palindrom
ist.
(e) element, welche angibt, ob ein gegebenes Element in einer Liste vorkommt.
(f) concat_all, welche alle Zeichenketten in einer gegebenen Liste von Zeichenketten miteinander verkettet.
(g) suffixe, welche jede Zeichenkette s auf eine Liste aller Suffixe von s abbildet.
(h) praefixe, welche jede Zeichenkette s auf eine Liste aller Präfixe von s abbildet.
Aufgabe 5.2 (Induktion auf Listen)
Für die folgenden Aufgaben gelten die Funktions-Definitionen aus der Vorlesung.
a. Bestimmen Sie durch schrittweise Reduktion die Werte der folgenden Ausdrücke:
(a)
append [1,4] (append [2] [3,5])
(b)
append (append [1,4] [2]) [3,5]
(c) len ( append [ 3 , 5 ] [ 7 , 0 ] )
(d) sum ( append [ 3 , 5 ] [ 7 , 0 ] )
(e) sortiert ( append [ 3 , 5 ] [ 7 , 0 ] )
(f) insert 6 ( append [ 3 , 5 ] [ 7 , 0 ] )
b. Zeigen Sie durch strukturelle Induktion, dass
(a) die Funktion append :: [a] -> [a] -> [a] assoziativ ist,
(b) für alle Listen xs, ys :: [ a ] gilt:
len ( append xs ys ) = len xs + len ys
(c) für jede Liste xs :: [ Int ] gilt:
sum ( doubles xs ) = 2 * ( sum xs )
(d) für jede Liste xs :: [ Int ] und jedes x :: Int gilt:
Aus sortiert xs folgt sortiert ( insert x xs )
(e) für die von Ihnenzu Aufgabe 5.1 entworfene Funktion rev und jede Liste xs
gilt: rev ( rev xs ) = xs.
Aufgabe 5.3 (List Comprehensions)
Definieren Sie die folgenden Funktionen mit Hilfe von List Comprehensions, geben Sie
jeweils den Typen der Funktion an und testen Sie ihre Implementierungen an ausdrucksstarken Beispielen.
a. lens, welche jede Liste von Zeichenketten auf die Liste der Längen dieser Zeichenketten abbildet,
b. nonempty, welche jede Liste von Listen auf die Liste aller in dieser Liste enthaltenen nichtleeren Listen abbildet,
c. sums, welche zu einer eingegebenen Liste von Listen natürlicher Zahlen die Liste
der Summen der Elemente der Einzellisten zurückgibt,
d. sums5, welche zu einer eingegebenen Liste von Listen natürlicher Zahlen genau
die Listen zurückgibt, deren Summe > 5 ist,
e. ct47, welche alle Beträge < 50 ct (jeden genau einmal in aufsteigender Reihenfolge) zurückgibt, die sich nur mit 4- und 7-ct-Münzen zahlen lassen.
Übungsaufgaben, Folien und weitere Hinweise zur Vorlesung finden Sie online unter
www.imn.htwk-leipzig.de/~schwarz/lehre/ss15/dp.