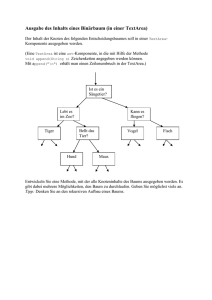
Westsächsische Hochschule Zwickau, Fachgruppe Informatik Prof. S
Werbung

Westsächsische Hochschule Zwickau, Fachgruppe Informatik Prof. S. Schwarz [email protected] 2.Übung zur Vorlesung Deklarative Programmierung“ ” Wintersemester 2011/2012 gestellt am 2. November 2011 Aufgabe 2.1 (Funktionen auf Listen) Definieren Sie die folgenden Funktionen (einschließlich Typdeklaration) a. rev, welche jede gegebene Liste l auf eine Liste der Elemente von l in umgekehrter Reihenfolge abbildet. b. palindrom, welche angibt, ob eine eingegebene Zeichenkette ein Palindrom ist. c. element, welche angibt, ob ein gegebenes Element in einer Liste vorkommt. d. concat_all, welche alle Zeichenketten in einer gegebenen Liste von Zeichenketten miteinander verkettet. e. suffix, welche jede Zeichenkette s auf eine Liste aller Suffixe von s abbildet. f. praefix, welche jede Zeichenkette s auf eine Liste aller Präfixe von s abbildet. Aufgabe 2.2 (Induktion auf Listen) a. Zeigen Sie durch schrittweises Ableiten (Papier), dass gilt: append [1,4] (append [2] [3,5]) = append (append [1,4] [2]) [3,5] b. Zeigen Sie, dass für alle Listen xs gilt append xs [] = xs. c. Zeigen Sie, dass append assoziativ ist, d.h. für alle Listen xs, ys, zs gilt: append xs (append ys zs) = append (append xs ys) zs d. Zeigen Sie, dass für Ihre oben entworfene Funktion rev und jede Liste xs gilt: rev (rev xs) = xs Aufgabe 2.3: Bestimmen Sie (ohne Computer) die folgenden Werte mit Hilfe der in der Vorlesung definierten Funktionen: • fsum double (twice double) 4 • twice twice twice succ 0, • twice twice twice twice succ 0 • ( double . (twice ( \ x -> 3 * x ) ) ) 2 Überlegen Sie sich zunächst für jeden Teilausdruck seinen Typ. Aufgabe 2.4: Wie lautet der (allgemeinste) Typ der Funktion twice twice für twice = \ f x -> f ( f x ) )? Aufgabe 2.5: Definieren Sie die folgenden Funktionen mit Hilfe passender Funktionen höherer Ordnung: a. squares, welche jede Liste natürlicher Zahlen auf die Liste der Quadratzahlen der Elemente der Eingabeliste abbildet. b. lens, welche jede Liste von Zeichenketten auf die Liste der Längen dieser Zeichenketten abbildet. c. nonempty, welche jede Liste von Listen auf die Liste aller in dieser Liste enthaltenen nichtleeren Listen abbildet. Aufgabe 2.6: Überlegen Sie (ohne Computer), welche Funktionen hier definiert werden: a. map (+2) b. foldr (&&) True c. foldr (\ x y -> x || (\ y -> mod y 2 == 0) ) False d. f xs = fold (+) 0 (map (\ x -> x * x) (filter (\ x -> (mod x 2 == 0) ) xs)) Überlegen Sie sich zunächst, welchen Typ die Funktionen haben und bestimmen Sie die Funktionswerte für einige geeignet gewählte Argumente. Aufgabe 2.7: Definieren Sie die folgenden Funktionen mit Hilfe von Funktionen höherer Ordnung a. für Peano-Zahlen: plus, mult, pot. b. für Listen: squares, welche jede eingegebene Liste von Zahlen auf die Liste aller Quadrate der Elemente der Eingabeliste abbildet, append, all_equal, kleinstes Element c. für Binärbäume: Anzahl der Blätter, Anzahl der inneren Knoten, Tiefe des Baumes, kleinster Schlüssel Aufgabe 2.8 (Funktionen auf Bäumen) Definieren Sie Funktionen zum a. Bestimmen der Liste aller Blätter eines binären Baumes b. Bestimmen der Summe aller Knoten eines binären Baumes (Schlüsseltyp: ganze Zahlen) c. Preorder-Duchlauf aller Knoten eines binären Baumes Aufgabe 2.9 (Induktion auf Bäumen) Zeigen Sie, das Ihre in der vorigen Aufgabe definierte Funktion zum Einfügen in einen binären Suchbaum die Suchbaum-Eigenschaft erhält. Übungsaufgaben, Folien und weitere Hinweise zur Vorlesung finden Sie online unter http://www.fh-zwickau.de/~sibsc/lehre/ws11/decprog/.