Halbleiterphysik (PSE 4).
Werbung

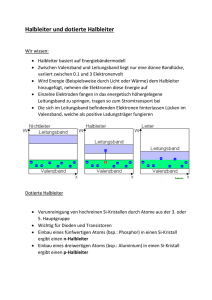
Fakultät Mathematik und Naturwissenschaften Professur für Didaktik der Physik Beleg zur Lehrveranstaltung „Physikalische Schulexperimente 4“ HALBLEITERPHYSIK Tom Köhler Eingereicht am 20. Juli 2010 2 ZUSAMMENFASSUNG Die technische Grundlage unserer inflationär anwachsenden Informationsgesellschaft bildet die Halbleiterindustrie. Und die wiederum wäre nichts ohne die Grundlagenforschung in der Halbleiterphysik. Besonders im Freistaat Sachsen, dem „Silicon Saxony“ mit dem weltweit bedeutenden Halbleiter-Standort Dresden, möchte man meinen, dass ein Abiturient mit verstärkter Physikausbildung (Leistungskurs) ein grundlegendes Wissen zur Halbleiterphysik und damit ein elementares Verständnis für die Vorgänge eines jeden Mikrochips mitbringt. Doch ein Blick in den sächsischen Lehrplan schafft Ernüchterung: die Leitungsvorgänge in Halbleitern verschwinden im Leistungskurs der Klassenstufe 11 in einer Wahlpflicht-Nische. Man könnte fast den Eindruck gewinnen, dass der Freistaat keine eigenen Bürger in dem für ihn so wichtigen Industriezweig sehen möchte. Es obliegt also der Verantwortung des Lehrers (und natürlich den Interessen von Schülern und Lehrer), sich auch in einem Leistungskurs Freiräume für einen Wahlpflichtbereich zu schaffen und somit dieses wichtige Thema hinreichend gut zu behandeln. 3 4 INHALTSVERZEICHNIS 1 Fachlicher Teil 1.1 1.2 1.3 7 Leitungsvorgänge in Halbleitern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.1 Das Bändermodell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.2 Eigenleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.1.3 Dotierte Halbleiter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Der p-n-Übergang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.2.1 Raumladungszone . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.2.2 Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 Transistoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.1 Bipolartransistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.3.2 Feldeffektransistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2 Didaktischer Teil 2.1 Lehrplanübersicht 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 2.2 Analyse des Lernbereichs „Leitungsvorgänge in Halbleitern“ (11 LK) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 2.2.1 Vorwissen und Lernschwierigkeiten . . . . . . . . . . . . . . . . . . . . . . 21 2.2.2 Gliederungsvorschlag . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 5 3 Experimente 25 3.1 Demonstrationsexperiment: Feldeffekttransistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 3.1.1 Aufbau und Durchführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 3.1.2 Ziele des Experiments und Einordnung in den Unterrichtsgang . . . . . . . 27 3.1.3 Vor- und Nachteile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 3.2 Schülerexperiment: Kennlinien einer Halbleiterdiode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 3.3 Das Brummen muss weg: Das Gleichrichter-Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 3.4 Eine intellektuelle Herausforderung: Der astabile Multivibrator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 3.5 Funktionsprinzip einer stabilisierten Spannungsquelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 4 Literatur 31 5 Anhang – Arbeitsblätter 33 6 Inhaltsverzeichnis 1 FACHLICHER TEIL 1.1 LEITUNGSVORGÄNGE IN HALBLEITERN 1.1.1 Das Bändermodell Um das Bändermodell zu beschreiben sind Ausflüge in die Quantenmechanik unumgänglich. Da der Grad der Komplexität nicht unnötig in die Höhe geschraubt werden soll, wird bereits an dieser Stelle eine leicht vereinfachte Darstellung gewählt. Betrachten wir zunächst das Bohrsche Atommodell, angewendet auf ein einzelnes, freies Atom. Dem Modell zufolge können sich die Elektronen nicht beliebig im Coulombpotential des Atomkerns aufhalten, sondern nur auf bestimmten Bahnen („Schalen“) mit klar definierten Energiewerten. Erhält ein Elektron beispielsweise durch thermische Anregung mehr Energie, so kann es in eine Schale höherer Energie gelangen, sofern diese Schale noch einen freien Zustand bereit hält. Wird das Elektron gar auf eine Energie E > 0 angeregt, so hat es das Coulombpotential des Kerns verlassen und kann sich außerhalb frei bewegen. Abbildung 1.1: Erlaubte Energieniveaus im Coulombpotential eines Wasserstoffkerns Halbleiter sind – wie Metalle auch – Festkörper mit einer symmetrischen Gitterstruktur. Die Atome besitzen ihren festen Platz in diesem Atomgitter und können diesen Platz im Allgemeinen nicht verlassen. Im Unterschied zum einzelnen, isolierten Atom treten nun vorrangig zwei Effekte auf, die unsere gerade geschaffene Anschauung etwas abändern. Erstens spalten sich die zulässigen Energieniveaus durch die gegenseitige Beeinflussung der Elektronen der verschiedenen Atome auf. Die Zahl der Aufspaltungen ist proportional zur Zahl der zusammenkommenden Atome. Im Fall unserer Gitterstrukturen, d.h. bei sehr vielen Atomen, entstehen damit mehrere getrennte, selbst aber quasi-kontinuierliche Energiebänder 1 . Der zweite Effekt ist, dass das Coulombpotential der einzelnen Atome nun nicht mehr asympto1 In diesen dicht gepackten Atomgittern sind die einzelnen Atome und ihre zugehörigen Elektronen ununterscheidbar. In der Quantentheorie werden die Elektronen daher als ein einziger, gebundener Zustand betrachtet und mit Wellenfunktionen (Schrödingergleichung) beschrieben, wobei sie im gesamten Kristall stehende Wellen bilden. Über die de-BroglieBeziehung p = λh wird den Wellen ein Impuls und damit eine kinetische Energie zugeordnet. Am „Boden“ eines jeden Bandes besitzen die Wellen den minimalen Impuls pmin , der bis zur oberen Grenze des jeweiligen Bandes zum maximalen Impuls pmax ansteigt. 8 Kapitel 1 Fachlicher Teil Abbildung 1.2: Aufspaltung der Energieniveaus in Energiebänder tisch gegen 0 ansteigt (siehe Abbildung 1), sondern vorher zum nächsten Nachbarn wieder „abbiegt“ (siehe Abbildung 3). Eine Folge dieses Effektes liegt auf der Hand: Die Elektronen können sich nun schon ab einer bestimmten Energie E < 0 frei von Atom zu Atom bewegen. Lediglich an der Oberfläche des Gitters verläuft das Potential gegen den Wert 0, sodass die Elektronen zumindest dort gebunden sind. Abbildung 1.3: Potentialwälle der Atomkerne mit lokalen Maxima Vmax < 0. Wie soeben beschrieben, besitzt das Coulombpotential zwischen jedem Gitteratom ein lokales Maximum Vmax < 0. Elektronen, die sich in Energiebändern mit E < Vmax befinden, sind an den jeweiligen Kern gebunden. Das letzte mit Elektronen besetze Band ist das sogenannte Valenzband 2 . Das nächst energiereichere Band nennt man das Leitungsband, das in Energiebereichen von E > Vmax liegt. 1.1.2 Eigenleitung Elektronenleitung Da Elektronen im Leitungsband so viel Energie besitzen, dass sie nicht im Potential der Gitteratome gefangen sind, können sie sich also außerhalb frei bewegen. Sobald ein elektrisches Feld im Gitter vorliegt, zum Beispiel durch Anlegen einer elektrischen Spannung, wird die stochastisch ungeordnete, thermische Bewegung (brownsche Bewegung) der Elektronen durch eine entlang des Feldes gerichtete Bewegung mit der sogenannten Driftgeschwindigkeit überlagert. Es kommt zum Stromfluss. 2 Streng genommen gilt das nur bei T = 0K, da sich bei einer Temperatur T > 0K stochastisch einige Elektronen auf Grund thermischer Anregung in einem höheren Energieniveau, also einem höheren Band, befinden. 1.1 Leitungsvorgänge in Halbleitern 9 Es wurde bereits gesagt, dass das Valenzband das letzte mit Elektronen besetzte Band ist. Wie gelangen die Elektronen nun in das Leitungsband? Bei metallischen Leitern zeigt sich, dass sich das Valenz- und das Leitungsband berühren oder gar überlappen. Damit sind die Valenzelektronen (also diejenigen im Valenzband) von Metallen immer auch schwach gebundene Leitungselektronen, was die gute elektrische Leitfähigkeit von Metallen erklärt. Abbildung 1.4: Leiter, Halbleiter und Isolatoren Bei Halbleitern (und Isolatoren) liegt eine gewisse Energielücke zwischen Valenz- und Leitungsband vor. Da Elektronen nicht ohne Anregung in ein höheres Energieniveau gelangen können, ist die Leitfähigkeit sehr gering oder verschwindet sogar. Wenn die Elektronen allerdings durch thermische Energie3 oder elektromagnetische Strahlung angeregt werden, so kann zumindest bei Halbleitern eine Elektronenleitung im Leitungsband erfolgen (bei Isolatoren ist die Energielücke so groß, dass es unter „normalen“ Bedingungen unmöglich ist eine signifikante Leitfähigkeit hervorzurufen). Löcherleitung Wenn ein Elektron durch Anregung in das Leitungsband gelangt (und dadurch frei wird), so hinterlässt es an seinem alten Platz einen freien Zustand, den man sich bildlich als ein „Loch“ im Energieniveau vorstellen kann – man spricht von der Erzeugung eines ElektronLoch-Paares. Dieses Loch kann nun von einem anderen Elektron wieder gefüllt werden, entweder von einem aus dem Leitungsband, das an Energie verliert, oder aber von einem gebundenen Elektron eines benachbarten Atoms, was durch den quantenmechanischen Tunneleffekt ermöglicht wird. Liegt ein elektrisches Feld an, so ist die Wahrscheinlichkeit sehr groß, dass ein Elektron gegen das Feld durch den Potentialwall tunnelt, den freien Zustand einnimmt und damit in Feldrichtung ein Atom weiter ein Loch entsteht. Dieser Effekt wird als Löcherleitung bezeichnet. Da die „gelöcherten“ Atome ein Elektron ins Leitungsband verabschiedet haben (wo sich die Elektronen ungebunden und frei bewegen können), herrscht nun ein Elektronenmangel. Das Atom wurde ionisiert und ist jetzt einfach positiv geladen. Daher sieht es bei der Löcherleitung von außen betrachtet auch so aus, als würde eine positive Ladung durch das Gitter wandern. 1.1.3 Dotierte Halbleiter Reine Halbleiter (z.B. Silizium, Germanium, etc.) sind unter Normalbedingungen nahezu nicht leitfähig, da zwischen ihrem (voll besetzten) Valenzband und dem Leitungsband eine Energielücke besteht. Um dennoch Einfluss auf ihre Leitfähigkeit zu nehmen, werden Halbleiter in der Technik 3 Daher 10 sinkt bei Halbleitern der elektrische Widerstand mit steigender Temperatur. Kapitel 1 Fachlicher Teil Abbildung 1.5: Modellhafte Vorstellung der Löcherleitung häufig dotiert. Dabei werden in das Gitter einige wenige Fremdatome eingebracht, die in ihrem vollen Valenzband entweder ein Elektron mehr (Donatoren) oder eines weniger (Akzeptoren) haben. Ein mit Donatoren dotierter Halbleiter besitzt also Fremdatome mit einem Valenzelektron mehr. Dieses zusätzliche Elektron wird zur Bindung mit den Nachbaratomen nicht benötigt und ist daher leicht ablösbar4 , d.h. es kann einfacher in das Leitungsband gelangen als die restlichen Valenzelektronen. Da Elektronen negativ geladen sind, spricht man in diesem Fall von n-dotierten Halbleitern. N-dotierte Halbleiter werden also durch Elektronenleitung leitfähig. Wird der Halbleiter mit Akzeptoren dotiert, so fehlt ein Elektron zur stabilen Bindung mit den Nachbaratomen, weshalb das Fremdatom nun doch noch ein Valenzelektron mehr aufnehmen kann. Dieses Loch ermöglicht wieder die oben beschriebene Löcherleitung. Da das Loch nach außen hin wie eine positive Ladung wirkt, bezeichnet man diese Halbleiter auch als p-dotiert. Es ist zu beachten, dass dotierte Halbleiter, egal welchen Typs, nach außen immer elektrisch neutral sind. Zwar besitzen beispielsweise n-dotierte Halbleiter je Frematom ein Elektron mehr, doch dieses Fremdatom besitzt auch ein Proton mehr im Kern. Diese Tatsache ist wichtig zum Verständnis der p-n-Übergänge. 1.2 DER P-N-ÜBERGANG Die beschriebenen Leitungsvorgänge sind an sich wenig spektakulär. Doch sie ermöglichen einen Effekt, der uns Menschen das Tor in das Zeitalter der technischen Moderne geöffnet hat. Dieser Effekt ist der sogenannte p-n-Übergang, der beim Zusammenführen je eines n- und p-dotierten Halbleiterkristalls an der Kontaktfläche entsteht. 4 Energetisch befindet befindet es sich unmittelbar unter dem Leitungsband. 1.2 Der p-n-Übergang 11 1.2.1 Raumladungszone Beide Kristalle sind zunächst nach außen elektrisch neutral. Der n-dotierte Halbleiter hat jedoch durch die zusätzlichen Elektronen der Donatoren eine höhere Dichte an freien Ladungsträgern als der p-dotierte Halbleiter. Fügt man nun beide Kristalle aneinander, so diffundieren einige Elektronen der n-Schicht5 in die p-Schicht und rekombinieren dort mit den freien Löchern der Akzeptoren, wo sie zunächst (nicht besonders stark) gebunden sind. Das geschieht jedoch nicht beliebig weit in den Kristall hinein. Da beide Kristalle zuvor elektrisch neutral waren, der n-Schicht jetzt aber einige Elektronen abhanden gekommen sind, existiert in dieser nun ein Elektronenmangel, also ein positiv geladener Bereich. Analog herrscht im Grenzgebiet der p-Schicht nun ein Elektronenüberschuss, sodass ein negativ geladener Bereich entsteht. Diese unterschiedlich geladenen Bereiche rufen ein elektrisches Feld hervor, dass einer weiteren Diffusion entgegenwirkt. Liegen Diffusion und die entgegenwirkende Coulomb-Kraft im Gleichgewicht, so spricht man bei den betroffenen n- und p-Bereichen, in denen die Diffusion stattfand, von einer Raumladungszone. Den Potentialunterschied des elektrischen Feldes nennt man auch Diffusionsspannung. Bei Silizium-Dioden beträgt sie etwa 0, 7 Volt. 1.2.2 Anwendungen Wir konstruieren uns nun ein Bauelement, das wie eben beschrieben aufgebaut ist: aus einem n-dotierten und einem p-dotierten Halbleiter, die beide eine Kontaktfläche haben und es so zur Ausbildung einer Raumladungszone kommt. Dieses Bauteil nennen wir elegant Diode. Welche Eigenschaften hat solch eine Diode? Wird die Diode in einen Stromkreis geschaltet, der mit Gleichspannung betrieben wird, so ergeben sich zwei Fälle: 1. Fall (+ an n und − an p): Der Pluspol der Spannungsquelle liegt an der n-Schicht an, der Minuspol an der p-Schicht. Dadurch werden die Elektronen der n-Schicht in Richtung des Pluspols 5 Also 12 Elektronen der n-dotierten Seite. Im Folgenden wird zur Abkürzung von n- und p-Schichten gesprochen. Kapitel 1 Fachlicher Teil gezogen. Die Raumladungszone wird vergrößert; das äußere E-Feld verstärkt, da es ja in die gleiche Richtung zeigt, das E-Feld der Raumladungszone. Den Elektronen der p-Schicht ist es somit nicht mehr (oder kaum noch) möglich, durch die verbreiterte Raumladungszone zu diffundieren, also gegen das elektrische Feld anzukommen. Es wird, wenn überhaupt, nur ein äußerst geringer Strom zu messen sein. Die Diode ist in Sperrrichtung geschaltet. 2. Fall (− an n und + an p): Der Pluspol der Spannungsquelle liegt an der p-Schicht an, der Minuspol an der n-Schicht. Das äußere elektrische Feld wirkt nun entgegen des inneren – die Raumladungszone wird verkleinert. Somit ist es den Elektronen aus der Spannungsquelle möglich, fortwährend durch die Zone zu diffundieren, in der p-Schicht zu rekombinieren und/oder vom Pluspol „abgesaugt“ zu werden. Dieser Stromfluss wird besonders stark ab einer angelegten Spannung, die in etwa der Diffusionsspannung entspricht. Die Diode ist in Durchlassrichtung geschaltet. Auf Grund der Tatsache, dass Dioden nur in einer Richtung Strom durchlassen, werden sie häufig als Gleichrichter eingesetzt, um aus einem Wechselstrom einen (pulsierenden) Gleichstrom zu machen. Zudem sind normale Dioden immer von einer lichtundurchlässigen Schutzschicht umhüllt, die ein Eindringen von Licht in den Halbleiter verhindern soll. Dieses Eindringen von Licht ist bei sogenannten Photodioden und Solarzellen jedoch erwünscht, weshalb ihre Halbleiter blank liegen oder nur eine lichtdurchlässige Schutzschicht haben. Denn das Licht sorgt im Halbleiter für den bekannten Photoeffekt, also für die Entstehung von ElektronLoch-Paaren – auch in der Raumladungszone! Diese Elektronen werden durch die Diffusionsspannung in Richtung n-Schicht beschleunigt. Schließt man die Photodiode in Sperrrichtung (!) an eine Spannungsquelle, so können diese Elektronen abgesaugt werden. Es fließt also genau dann ein Strom durch die in Sperrrichtung geschaltete Photodiode, wenn Licht auf sie trifft. Sie kann damit als Lichtsensor verwendet werden. Solarzellen bestehen aus vielen Photodioden, an denen allerdings keine äußere Spannung angelegt wird. Trifft Licht auf die Photodioden, so ändert sich das E-Feld in der Raumladungszone. Diese Differenz zum vorherigen Potentialunterschied wird abgegriffen und zur Stromerzeugung genutzt. Die mit Abstand bedeutendsten Anwendungen bieten Transistoren, die aus mehreren p-n-Übergängen bestehen. Ihnen wird nun ein eigener Abschnitt gewidmet. 1.3 TRANSISTOREN Konrad Zuse entwickelte 1941 den ersten programmierbaren Digitalrechner der Welt – seinen Zuse Z3. Für seine Flipflops und logischen Schaltungen nutzte er mechanisch arbeitende Relais. Im Deutschen Museum in München steht ein Nachbau dieses Rechners, den man nicht nur sehen, sondern bei Inbetriebnahme vor allem hören kann. Die Schränke voller Relaisbänke klackern bei jeder Eingabe, Berechnung und Ausgabe munter vor sich hin. Aus heutiger Sicht hat diese geniale Leistung Zuses etwas bewundernswertes, doch schon damals stand fest, dass diese Mechanik nicht die Zukunft sein kann. Schon bald darauf nutzte man kompaktere Transistoren als elektrische Schalter, die schneller und vor allem lautlos arbeiteten. Doch auch in der Verstärkertechnik, 1.3 Transistoren 13 v. a. im Rundfunk und der Musikbranche, lösten die Transistoren zunehmend die alten Elektronenröhren als Verstärker ab. Transistoren können also als Schalter und Verstärker dienen. Ihre Funktionsweise wird im folgenden beschrieben. Es gibt mehrere Arten von Transistoren. Die bekanntesten, aus drei Schichten bestehenden Transistortypen sind die Bipolar- und die Feldeffekttransistoren. 1.3.1 Bipolartransistor Bipolartransistoren sind Bauelemente mit drei abwechselnd dotierten, aufeinander folgenden Schichten. Die Schichtungsreihenfolge ist also entweder n-p-n oder p-n-p. Es sind sogenannte stromgesteuerte Transistoren, die den Stromfluss in einem Hauptstromkreis durch den (schwachen) Strom eines Nebenstromkreises steuern. Die drei Anschlüsse – an jeder Schicht einer – werden mit Kollektor (C), Basis (B) und Emitter (E) bezeichnet, wobei die Basis immer die mittlere Schicht ist. Abbildung 1.6: Schaltzeichen der Bipolartransistortypen Funktionsweise Durch die drei abwechselnd dotierten Schichten entstehen an den Grenzen zwei Raumladungszonen mit entgegengesetzten, elektrischen Feldern. Legt man an Emitter und Kollektor eine Spannung an, so könnte kein Strom fließen – eine der Raumladungszonen sperrt den potentiellen Stromfluss. Um dennoch einen Stromfluss zu ermöglichen, kommt die Basis ins Spiel. Im Folgenden wird die Funktionsweise eines n-p-n-Bipolartransistors beschrieben. Ein p-np-Transistor funktioniert analog, jedoch müssen zur Erklärung sämtliche Spannungen und Stromrichtungen umgedreht werden. Denken wir uns zunächst im Kollektor-Emitter-Stromkreis eine Spannung so angelegt, dass der Pluspol am Kollektor und der Minuspol am Emitter anliegt. Es kann kein Strom fließen, da die Kollektor-Basis-Grenzschicht sperrt. Wird an den Basis-Emitter-Kreis ebenfalls eine Spannung mit Pluspol an der Basis angelegt (siehe Abbildung 7), so ist ein Stromfluss zwischen Basis und Emitter möglich. Nun kommt das entscheidende Baumerkmal der Bipolartransistoren zum Tragen: Die Basis-Schicht ist äußerst schmal und nur schwach dotiert. Die zahlreichen Elektronen aus dem stark dotierten 14 Kapitel 1 Fachlicher Teil Abbildung 1.7: Funktionsweise des Bipolartransistors Emitter können durch die verkleinerte Raumladungszone an der Emitter-Basis-Schicht diffundieren. Da die Basis nur eine schwache Dotierung aufweist, kann nur ein kleiner Teil der Elektronen (ca. 1%) mit den Löchern der Basis rekombinieren. Da die Basis-Schicht zudem sehr schmal ist, diffundieren die Elektronen trotz der verbreiterten Raumladungszone weiter zum Kollektor, wo sie schließlich zum Pluspol der Spannungsquelle abgezogen werden. Noch einmal in der Zusammenfassung: Liegt lediglich eine Spannung zwischen Emitter und Kollektor an, so kann zwischen ihnen kein Strom fließen. Sobald aber ein (sehr kleiner) Strom über die Basis zum Emitter fließt, dann fließt auch ein Strom vom Kollektor zum Emitter. Dies erklärt die Schalter-Fähigkeit eines Transistors. Da außerdem die Stromstärke im Kollektor-EmitterStromkreis abhängig von der Stärke des Basis-Emitter-Stroms ist, kann der Transistor auch als stufenloser Regler genutzt werden. Das ist zugleich auch die Erklärung für die Verstärker-Wirkung eines Transistors: Fließt zwischen Basis und Emitter ein pulsierender Strom (z. B. der schwache Induktionsstrom eines dynamischen Mikrophons), so pulsiert der mitunter viel stärkere Strom im Kollektor-Emitter-Stromkreis in gleicher Weise mit. 1.3.2 Feldeffektransistor Man bemerkte schnell, dass sich Transistoren hervorragend für große, komplexe Schaltungen nutzen lassen. Doch ebenso schnell war klar, dass der jeweils sehr kleine Basisstrom in der Summe zu einer nicht unerheblichen Leistungsaufnahme führt. Also machte man sich Gedanken, wie man Transistoren mit einer angelegten Spannung statt mit einem Strom steuern könnte. Feldeffekttransistoren (FET) sind spannungsgesteuerte Transistoren. Ihr Aufbau ist auf den ersten Blick dem der Bipolartransistoren recht ähnlich. Auch sie bestehen aus zwei n-Schichten und einer p-Schicht oder zwei p-Schichten und einer n-Schicht (siehe Abbildung 8). Es gibt viele Arten von Feldeffekttransistoren. Die gängigsten sind die sogenannten Metall-OxidHalbleiter Feldeffekttransistoren (MOSFET). Deren äußere Anschlüsse sind direkt mit den beiden gleich dotierten Schichten verbunden. Über sie fließt der zu regelnde Strom, der vom SourceKontakt (S, Quelle) zum Drain-Kontakt (D, Senke) fließt. Zwischen den beiden Schichten liegt die 1.3 Transistoren 15 Abbildung 1.8: Aufbau eines MOSFET komplementär dotierte Schicht. Der dritte Anschluss ist jedoch nicht direkt mit ihr verbunden, sondern durch eine dünne Isolationsschicht getrennt – es soll ja kein Stromfluss erfolgen. Der dritte Kontakt wird als Gate (G, Tor) bezeichnet. Über ihn wird der Transistor gesteuert. Da Spannung immer Potentialdifferenz bedeutet, gibt es an MOSFETs häufig noch einen vierten, dem Gate gegenüberliegenden Anschluss. Dieser wird mit Bulk (B) bezeichnet. Oftmals wird dieser Anschluss jedoch intern mit Source verbunden, da es ausreicht, nur am Gate ein Potential anzulegen und da eine Spannungsdifferenz zwischen Source und Bulk meist unerwünscht ist. Abbildung 1.9: Schaltzeichen der Feldeffekttransistortypen Funktionsweise Es wird die Funktionsweise eines n-Kanal-MOSFET erklärt, bei dem die mitt- lere Schicht p-dotiert ist und die Stromanschlüsse an n-dotierten Schichten anliegen. Der p-KanalMOSFET funktioniert natürlich wieder analog. Liegt zwischen Gate und Bulk keine Spannung an oder liegt das Gate auf dem gleichen Potantial wie die mittlere p-Schicht, so fließt kein Strom zwischen Source und Drain, da wieder zwei entgegen ausgerichtete Raumladungszonen an den Schichtübergängen vorherrschen, von denen eine sperrt (siehe Abbildung 8). Man sagt, der Transistor ist selbstsperrend oder normal-sperrend 6 . Erhält das Gate nun ein positives Potential (gegenüber Bulk oder dem Rest des Transistors) entsteht um das Gate herum ein elektrisches Feld, das auch in die mittlere p-Schicht hineinreicht. 6 Es gibt auch MOSFETs, die selbstleitend (normal-leitend) sind, also bei nicht angelegter Spannung bereits leiten. Um den Rahmen dieser Arbeit nicht unnötig zu dehnen, beschränken wir uns auf die selbstsperrenden MOSFETs. 16 Kapitel 1 Fachlicher Teil Dieses Feld führt zu einem gewissen Effekt, daher der Name „Feldeffekttransistor“. Der Effekt ist folgender: Einige Elektronen der p-Schicht wandern in Richtung des Gates, also zum positiven Potential. Durch das Feld werden diese Elektronen ins Leitungsband angehoben, wodurch ihnen diese Wanderung ermöglicht wird. Dank der Isolationsschicht können sie jedoch nicht zum Gate direkt gelangen. In der Nähe des Gates rekombinieren sie mit den Löchern der p-Schicht. Von außen betrachtet wirkt es daher so, als würden die Löcher vom Gate weg gedrängt. Ist die angelegte Spannung (bzw. das positive Potential am Gate) groß genug, dann sind die Löcher so weit verdrängt worden, dass sie nicht mehr für eine Rekombination zur Verfügung stehen. Am Gate (natürlich noch vor der Isolationsschicht) bildet sich damit in dem eigentlichen p-Kristall ein n-leitender Bereich aus. Abbildung 1.10: MOSFET mit angelegter Gate-Spannung Dieser n-leitende Bereich bildet einen Kanal zwischen den n-dotierten Schichten an Source und Drain, wodurch zwischen diesen ein Stromfluss ermöglicht wird. Der Name dieses Transistortyps, nämlich n-Kanal-MOSFET, wird nun auch verständlich. Der entscheidende Vorteil der Feldeffekttransistoren gegenüber den Bipolartransistoren besteht also darin, dass die Steuerung des Hauptstromes durch das Variieren des am Gate anliegenden Potentials erreicht wird. Es fließt kein Steuerstrom. Daher gelten Feldeffekttransistoren als weitgehend verlustfrei. 1.3 Transistoren 17 18 Kapitel 1 Fachlicher Teil 2 DIDAKTISCHER TEIL 2.1 LEHRPLANÜBERSICHT Die Gymnasiasten in Sachsen werden laut dem überarbeiteten Lehrplan von 2009 nur maximal drei mal mit Halbleitern konfrontiert. In Klasse 8, Lernbereich 3 „Eigenschaften elektrischer Bauelemente“, untersuchen die Schüler das Temperaturverhalten und die I(U)-Kennlinien von ohmschen Bauelementen und reinen Halbleitern. In die eher anwendungsorientierte Elektronik geht es dann in Klasse 9, Lernbereich 1 „Grundlagen der Elektronik“. Hier lernen die Schüler die Grundlagen der Halbleitertechnik und einige Anwendungen kennen. Interessant: Während im Lehrplan von 2007 hier lediglich ein „Hinweis auf pn-Übergang“ gefordert war, ist der Übergang in der 2009er Fassung nun fest verankert. Für die meisten Schüler endet an dieser Stelle leider die Ausbildung im Halbleiterbereich. Nur im Wahlpflichtbereich 2 des Leistungskurses Klasse 11 tauchen noch einmal „Leitungsvorgänge in Halbleitern“ auf. Die folgende Tabelle gibt einen Überblick über die Themen in den jeweiligen Klassenstufen. Klassenstufe 8 Lernbereich und wichtige Inhalte LB 3: Eigenschaften elektrischer Bauelemente Abhängigkeit des elektrischen Widerstands von der Temperatur bei Metallen und Halbleitern, I(U)-Kennlinien von Metallen und (reinen) Halbleitern 9 LB 1: Grundlagen der Elektronik Aufbau und Herstellung von Halbleitern, Grundlagen der Leitungsvorgänge (Dotierung, n- und p-Leitung), typische Halbleiterbauelemente (Dioden, Transistoren), Schaltungen zum Untersuchen von Eigenschaften und für Anwendungen 11 (LK) WP 2: Leitungsvorgänge in Halbleitern Leitungsvorgänge (Bändermodell mit Bandaufspaltung, Eigenleitung, n- und p-Leitung), Dioden, Bipolar- und Feldeffekttransistoren (Funktionsweise, Kennlinien, Anwendungen), Beispiele für logische Schaltungen 2.2 ANALYSE DES LERNBEREICHS „LEITUNGSVORGÄNGE IN HALBLEITERN“ (11 LK) Der Lernbereich „Leitungsvorgänge in Halbleitern“ ist lediglich im Leistungskurs der Klassenstufe 11 vertreten und dort auch nur als Wahlpflichtbereich. Da ich grundsätzlich die Meinung vertrete, dass Wahlpflichtbereiche – sofern überhaupt noch Zeit für sie bleibt – in Absprache mit den Schülern ausgewählt werden sollten, muss sich dieser Lernbereich mit den zwei anderen, ebenfalls sehr interessanten Bereichen „Physik des Fahrens“ und „Wechselstromkreis“ messen. In Anbetracht der Bedeutung der Halbleiterphysik für den Freistaat Sachsen und insbesondere für 20 Kapitel 2 Didaktischer Teil den Halbleiterstandort Dresden ist eine leichte Beeinflussung der Schülerwünsche zu Gunsten des hier vorzustellenden Lernbereichs sicherlich zu rechtfertigen. Der fachliche Teil der vorliegenden Arbeit lag bereits auf einem weniger hoch angesiedelten Niveau, welches daher auch in gleicher Weise für einen Leistungskurs geeignet sein sollte. Das Vorwissen der Schüler bietet dafür gute Voraussetzungen und auch neue Themen wie die Bandaufspaltung als Grundlage des Bändermodells sind für die Schüler zumutbar. 2.2.1 Vorwissen und Lernschwierigkeiten Atommodell Voraussetzung für die Behandlung des Bändermodells ist ein hinreichend gutes Atommodell, welches die Bewegungen der Elektronen auf bestimmten Energiebahnen mit bestimmten Energiewerten beschreibt. Gut geeignet wäre das Bohrsche Atommodell, doch das wird erst in Klasse 12 ausführlich behandelt. Ein Blick in den sächsischen Chemie-Lehrplan (2009) gibt aber Entwarnung: Im Lernbereich 2 des Grundkurses Klasse 111 , „Chemie der Nebengruppenelemente“, wird das Bohr-Sommerfeldsche Atommodell eingeführt. Die Schüler müssen dieses Atommodell zwar nur „kennen“, dennoch gehen die Inhalte dieses erweiterten Bohrschen Modells weit über das hinaus, was in Physik in Klasse 12 behandelt wird. Es greift viel tiefer in die quantenmechanischen Vorgänge ein2 . Bandaufspaltung Die zentralen Themen, also die p- und n-Leitung sowie der p-n-Übergang, kennen die Schüler bereits aus Klasse 9. Es darf jedoch nicht erwartet werden, dass das Wissen nach über 2 Jahren bei jedem Schüler abrufbereit ist. Eher das Gegenteil wird der Fall sein. Richtig problematisch dagegen kann es beim Bändermodell werden, insbesondere bei der Bandaufspaltung. Die Aufspaltung der einzelnen Elektronenbahnen in breite Energiebänder ist nicht ohne weiteres sofort einzusehen. In dem Lehrbuch „Metzler Physik“ (2. Auflage) bedient man sich eines mechanischen Analogons, bei dem mehrere gekoppelte Pendel, die alle eine spezifische Eigenfrequenz haben, von außen periodisch angeregt werden. Bei N gekoppelten Pendeln stellen sich N mögliche Resonanzfrequenzen ein, was der Aufspaltung entsprechen soll. Mal abgesehen davon, wie im Bereich der Atome nun die äußere, periodische Anregung erklärt werden soll, eignet sich das Analogon auch schlicht deshalb schlecht, weil solche komplexeren Schwingungssysteme erst in Klasse 12 behandelt werden. Einen Ausweg aus dieser Misere bietet abermals der bereits erwähnt Lernbereich „Chemie der Nebengruppenelemente“ aus dem Grundkurs Chemie, Klasse 11. Im Gegensatz zum Bohrschen Atommodell wird im Bohr-Sommerfeldschen Modell bereits die intrinsische Aufspaltung der Elektronenbahnen eines einzelnen Atoms beschrieben, was u. a. auf Wechselwirkung zwischen den Elektronen des Atoms zurückzuführen ist. Mit diesem Vorwissen sollte es möglich sein, den Schülern qualitativ klar zu machen, dass die Wechselwirkungen mit weiteren Atomen zu weiteren Aufspaltungen führt. 1 Ein Leistungskurs-Physik-Schüler wird mit Sicherheit lediglich einen Grundkurs Chemie besuchen dem Pauli-Prinzip u. a. auch Hundsche Regel. 2 Neben 2.2 Analyse des Lernbereichs „Leitungsvorgänge in Halbleitern“ (11 LK) 21 p-n-Übergang Das Bändermodell wird zunächst nur zur Erklärung der Leitungsvorgänge in rei- nen und dotierten Halbleitern herangezogen. Viele Lehrbücher (u. a. auch „Metzler Physik“) greifen auch beim p-n-Übergang auf das Bändermodell zurück, was durchaus auf Verständnisprobleme stoßen kann. Betrachtet man den Übergang im Bändermodell, so muss auf mehrere Dinge gleichzeitig geachtet werden: Je nachdem, welchen Bereich des Übergangs man gerade betrachtet (p-Leiter, n-Leiter, Raumladungszone), muss man sich im Klaren sein, wie die Ladungsverteilung und das entsprechende Potential aussieht und wie die Bänder letztlich im Energiediagramm liegen. Zudem muss man beachten, in welchen Energiebereichen die Donaten und die Akzeptoren liegen und am Ende auch noch, wie sich die Energiebänder vertikal verschieben, wenn eine äußere elektrische Spannung angelegt wird. Da im schulischen Bereich in der Halbleiterphysik ohnehin meist nur qualitative Aussagen gemacht werden, genügt meines Erachtens die einfachere Erklärung aus dem fachlichen Teil, die auf das Bändermodell verzichtet und lediglich mit den Begriffen „Diffusion“ und „Elektrisches Feld“ auskommt – beides Begriffe, die den Schülern wohl bekannt sind. Die Diffusion der Elektronen ist sehr plausibel. Die Schüler kennen bereits seit Klasse 7 das Elektronengasmodell und natürlich die Diffusion bei normalen Gasen. Das Elektronengas verhält sich nun ähnlich wie ein richtiges Gas: Obwohl n- und p-Schicht jeweils elektrisch neutral sind, so ist die Elektronenkonzentration im n-Leiter gegenüber der im p-Leiter leicht erhöht, weshalb einige Elektronen in die p-Schicht diffundieren. Die daraus resultierenden Ladungsverteilungen erzeugen ein elektrisches Feld, das einer weiteren Diffusion entgegenwirkt. Legt man eine äußere Spannung an, so wird das Feld je nach Polung entweder verstärkt (Sperrrichtung) oder abgeschwächt (Durchlassrichtung). Transistoren Bereits in Klasse 9 wurden Versuche mit Transistoren durchgeführt, jedoch nicht ihre Funktionsweise erklärt. Das ist auch erst mit einem tieferen Verständnis für den p-n-Übergang möglich. Beim Bipolartransistor treffen nun sogar drei Schichten aufeinander, was vielen Schülern Schwierigkeiten bereitet, die Funktionsweise nachzuvollziehen. Dieser intellektuellen Herausforderung muss sich ein Leistungskursschüler einfach selbst stellen. Ein Lehrer mag die Funktionsweise vielleicht wunderbar erklären können, sodass der Schüler das Gefühl hat, alles verstanden zu haben. Doch das hat er erst, wenn er es selbst einwandfrei erklären kann, und das ist selten sofort der Fall. Der Schüler muss sich ganz einfach selbst hinsetzen und sich in die Materie vertiefen. Das komplexe Zusammenspiel der dotierten Schichten, Ströme und Raumladungszonen muss sich jeder Schüler noch einmal selbst verinnerlichen. Ein viel trivialeres Verständnisproblem tut sich oftmals bei den Anwendungsgebieten der Transistoren auf. So wird häufig gelehrt, dass Transistoren als „Schalter, Regler oder Verstärker“ dienen. Der Lehrer sollte hierbei ausdrücklich betonen, dass, wie im fachlichen Teil beschrieben, diese drei Möglichkeiten ein und dasselbe sind. Ein Transistor ist zugleich Schalter und Verstärker (und durch die stetige Zunahme des Kollektor-Emitter-Stroms mit dem Basis-Emitter-Strom auch noch ein Regler). 22 Kapitel 2 Didaktischer Teil 2.2.2 Gliederungsvorschlag Im Rahmen des Lernbereiches sollten nicht nur die theoretischen Grundlagen der Halbleiterphysik behandelt, sondern auch Anwendungsbeispiele aufgezeigt und besprochen werden. Letzteres entfällt im Lehrplan leider gänzlich; lediglich zu integrierten Schalten sollen einige Schaltungsbeispiele betrachtet werden, die aber eher Schaltprinzipien darstellen und alleine nicht in einem Experiment zur Anwendung kommen können. Im Kapitel „Experimente“ werden mehrere anwendungsbezogene Versuche vorgestellt, von denen einer zu Beginn des Lernbereiches vorgeführt werden kann, um damit ein klares Ziel zu setzen: Dieses Verhalten soll erklärt werden. Einen hohen Motivationseffekt könnte auch das beschriebene Demonstrationsexperiment mit dem MOSFET haben. Die Schüler kennen das Bauelement des Feldeffekttransistors möglicherweise noch nicht und können sich damit das Verhalten der äußerst einfachen Schaltung nicht erklären. Damit ist bereits in den ersten Minuten das Ziel des gesamten Lernbereiches abgesteckt. Der Weg zum Verständnis führt systematisch über die Leitungsvorgänge in Halbleitern. Als Grundlage wird das Bohr-Sommerfeldsche Atommodell, dass die Schüler aus dem Chemie Grundkurs kennen, wiederholt. Mit dem Modell nähern wir uns behutsam der Bandaufspaltung und gelangen schließlich zum Bändermodell, welches bereits die Eigenleitung von reinen Halbleitern (sowie das Temperaturverhalten) erklären kann. Im Anschluss wird die Dotierung wiederholt, mit der die Leitungsvorgänge beeinflusst werden können. Das sind die Grundlagen für alles Weitere. Es folgt eine vertiefte Betrachtung des p-n-Übergangs, der uns zum Anwendungsbereich der Dioden führt. Hier könnte ein Schwerpunkt abseits der Lehrplanvorgaben gesetzt werden, in dem man im Rahmen der Umwelterziehung den Sinn und Nutzen von Solarzellen erörtert, was in der aktuellen Energieproblematik sicher viel Diskussionsstoff liefert. Wir können aber auch zielstrebig weiter unser Ziel verfolgen – das Eingangsexperiment verstehen. Mit Dioden ist das noch nicht möglich. Zu Zielerreichung kann nun die Behandlung der Feldeffekttransistoren angeschlossen werden. Häufig sind zwar zuerst die Bipolartransistoren an der Reihe, doch es gibt keinen Grund, diese Reihenfolge einzuhalten. Feldeffekttransistoren kommen bei der Erklärung ihrer Wirkungsweise mit dem Begriff des elektrischen Feldes aus – somit kommt man mit einfachen Mitteln soweit, dass man zum einen das Experiment erklären, zum anderen aber auch viele weitere Anwendungen (auch integrierte Schaltungen) untersuchen kann. Da es auch Anwendungsbeispiele gibt, wo von Steuerung des Transistores mit Hilfe eines Steuerstroms (statt einer Steuerspannung) sinnvoll wäre, wird im Anschluss noch der Vollständigkeit halber der Bipolartransisor untersucht – als intellektueller Höhepunkt und Abschluss des Lernbereichs und wahrscheinlich des Schuljahres. 2.2 Analyse des Lernbereichs „Leitungsvorgänge in Halbleitern“ (11 LK) 23 24 Kapitel 2 Didaktischer Teil 3 EXPERIMENTE Ich bin der Auffassung, dass innerhalb eines Wahlpflichtbereiches mehr anwendungsbezogene Experimente stehen sollten, die eher einen Motivationsschub leisten können als Experimente zu Kennlinien, die lediglich einen tieferen Einblick in die Eigenschaften der Bauelemente gestatten. Bei einem einzelnen p-n-Übergang, also einer Diode, mag die Untersuchung der Kennlinien sicherlich noch Sinn machen, vor allem wenn man einen Schwerpunkt auf das Verständnis des Übergangs legt. Bei Transistoren grenzt ein Untersuchen der Kennlinien fast schon an fanatische Detail-Liebe. Immerhin gibt es zahlreiche Kombinationen, in denen man die Zusammenhänge der Ströme und Spannungen der drei Anschlüsse untereinander untersuchen kann. Diese Kennlinien mögen für die Hersteller und die Industrie von ausschlaggebender Bedeutung sein, für den Schüler und auch den Lehrer sind sie eher ermüdend, zumal sie keinen wesentlichen Wissensfortschritt bieten. An die blinkenden LEDs eines astabilen Multivibrators wird sich ein Schüler wohl eher mal wieder erinnern als an die spannenden1 Kennlinien eines 20-Volt-Feldeffekttransistors. 3.1 DEMONSTRATIONSEXPERIMENT: FELDEFFEKTTRANSISTOR Mit Hilfe eines MOSFET lässt sich eine äußerst einfache und sehr verblüffende Schaltung aufbauen, die so manchen Beobachter in Staunen versetzen und zum Grübeln anregen kann. 3.1.1 Aufbau und Durchführung Für den Versuch wird ein MOSFET mit möglichst hoher Gatespannungstoleranz2 und eine einfache 6V-Glühbirne in Reihe geschaltet. Als Spannungsquelle dient ein Stromversorgungsgerät oder, als mobile Variante, eine Flach- oder Blockbatterie. Der Lehrer muss die Kabel selbst an den Anschlüssen des Transistors anlöten. Am Gate-Anschluss wird ein kleines, offenes Kabel als „Antenne“ angelötet. Zu beachten ist, dass der Source-Anschluss an den Minuspol angeschlossen wird. Im Prinzip sollten die MOSFETs zwar symmetrisch funktionieren, jedoch werden sie meist mit einer asymmetrischen Struktur hergestellt. Besonders wichtig beim Umgang mit MOSFETs ist es, sich vor dem Berühren der Transistoren zu erden. Ist man statisch aufgeladen und berührt das Gate, welches nur eine gewisse Spannung verträgt (z.B. 20 Volt), kann es sein, dass durch die Entladung des Körpers eine viel zu hohe Spannung auf das Gate gelangt und der Transistor unbrauchbar wird! Zur Durchführung gibt es mehrere Möglichkeiten. Bei einem selbstsperrenden Transistor leuchtet die Lampe zunächst nicht. Der Lehrer greift nun mit einer Hand an das offene Ende der Antenne (die mit dem Gate verbunden ist) und mit der anderen Hand an einen Kontakt mit einem beliebigen Potential, zum Beispiel an offene Kontaktstellen der Spannungsquelle, womit er das Potential auf das Gate überträgt. Die Lampe leuchtet nun. Wenn der Lehrer trockene Hände hat kann er 1 Achtung: Ironie! Beispiel der selbstsperrende n-Kanal MOSFET BUZ 11 FAI, erhältlich bei Conrad. Er verträgt Gatespannungen bis maximal 20 Volt. Im abgebildeten Schaltplan wurde auch das spezielle Schaltzeichen dieses Transistortyps verwendet. 2 Zum 26 Kapitel 3 Experimente Abbildung 3.1: Schaltplan des Demonstrationsexperiments auch versuchen, die Kontakte nur schwach zu berühren. Somit wird die Lampe nur schrittweise heller – der Lehrer fungiert quasi als Dimmer. Ein Berühren des Minuspols schaltet die Lampe wieder aus. Besonders eindrucksvoll ist jedoch die Dimmwirkung, die mittels Influenz erzeugt werden kann. Man bringt die Lampe zunächst auf mittlere Helligkeit. Nun reibt man einen Stab, sodass dieser elektrostatisch aufgeladen wird und bringt diesen Stab vorsichtig in die Nähe der Antenne, in welcher Ladungsträger auf Grund von Influenz getrennt werden, wodurch am Gate wieder ein Potentialzuwachs oder -abfall stattfindet, der die Lampe heller bzw. dunkler leuchten lässt. Entfernt man den Stab wieder, so leuchtet die Lampe wieder in ihrer mittleren Helligkeit. Wichtig ist hier wieder, dass der Stab nicht zu nah an die Antenne gebracht wird, da sonst das Potential am Gate zu groß und der Transistor zerstört werden kann. Daher wird die Lampe vorher auch auf mittlere Helligkeit gebracht, da man manchmal vorher nicht weiß, wie der Stab geladen ist – die Lampe könnte heller oder dunkler werden. 3.1.2 Ziele des Experiments und Einordnung in den Unterrichtsgang Der Versuch ist einerseits ein schönes Beispiel für die Anwendung von Feldeffekttransistoren. Häufig werden ja nur Experimente gezeigt, die mit Bipolartransistoren durchgeführt werden. Diese Transistoren haben in diesem Versuch allerdings keine Wirkung. Der wesentlich entscheidendere Nutzen des Experiments ist jedoch sein Motivationspotential. Und genau mit diesem Ziel kann er auch im Unterricht eingesetzt werden. Entweder bei der Behandlung der Feldeffekttransistoren oder aber als motivierender Einstieg in den Lernbereich mit dem Ziel im Ausblick, das Verhalten der Lampe erklären zu können. Der Versuch könnte dann an passender Stelle im Unterrichtsgang wiederholt werden. 3.1 Demonstrationsexperiment: Feldeffekttransistor 27 3.1.3 Vor- und Nachteile Der entscheidende Vorteil des Versuchs wurde bereits genannt: Er begeistert. Zudem ist er schnell und einfach aufgebaut, sehr übersichtlich und auch schnell mal durchgeführt. Man kann also mit wenig Aufwand in kurzer Zeit viel Aufmerksamkeit erreichen und Motivation hervorrufen. Der Versuch hat aber auch einige Nachteile. Zum einen ist er relativ klein und von weitem nur schlecht zu sehen. In größeren Klassen könnte das problematisch werden, doch Leistungskurse Physik bestehen häufig nur aus sehr wenigen Schülern, wo es kein Problem ist, die Schüler zu sich vor an den Lehrertisch zu holen. Abmilderung kann auch die Vorgabe des Schaltplans schaffen, wobei man das Schaltzeichen für den FET durch ein geeignetes „unbekanntes Bauelement“ ersetzen muss, wenn man den Versuch zu Beginn des Lernbereiches vorführen möchte. Auch der Transistor selbst ist (baubedingt) sehr klein, weshalb sich alternativ auch eine Übertragung des Versuchs mittels Kamera und Beamer anbietet. Ein weiterer Nachteil ist die Gatespannungstoleranz. Bei vielen Transistoren liegt diese im Millivoltbereich – für den Versuch sind solche Transistoren also gänzlich unbrauchbar. Hier muss der Lehrer vorher sorgfältig auswählen. Der Versuch sollte daher auch immer ein Demonstrationsversuch bleiben, da es Schüler (z. B. bei der Influenz) gern einmal zu weit treiben. 3.2 SCHÜLEREXPERIMENT: KENNLINIEN EINER HALBLEITERDIODE Bei einer Halbleiterdiode macht es durchaus Sinn, die I(U)-Kennlinien in Durchlass- und Sperrrichtung zu untersuchen, um das Verhalten des p-n-Übergangs zu studieren. Der Versuch wird bereits in Klasse 9 durchgeführt. Hier bietet er sich jedoch erneut an, um einen Vergleich zur Theorie des p-n-Übergangs zu ziehen, z. B. um die Diffusionsspannung zu ermitteln. Abbildung 3.2: Schaltplan zum Ermitteln der Kennlinie Zur Durchführung nutzt man eine Gleichspannungsquelle, die sowohl einen hohen Spannungsbereich abdecken kann (ca. 20 Volt) als auch feine Einstellungen (0,1 Volt Abstände) zulassen. Alternativ kann, da es ein Schülerexperiment sein soll, auch eine Spannungsquelle mit grober Abstufung und ein Potentiometer verbaut werden. Wichtig ist, dass vor die Diode ein Schutzwiderstand geschaltet wird. 28 Kapitel 3 Experimente Bevor man die Messung beginnt, sollte man sich überlegen, in welchen Spannungsbereichen man arbeiten muss und welche Stromstärken zu erwarten sind. Bei Siliziumdioden beträgt die Diffusionsspannung etwa 0,7 Volt, daher sollte die Arbeitsspannung in Durchlassrichtung maximal in diesem Bereich liegen. Die Stromstärke bleibt zunächst bei Null, steigt dann jedoch rasch an. Bei Messungen in Sperrrichtung sind höhere Spannungen nötig; die Ströme bleiben sehr klein. Ein mögliches Arbeitsblatt ist im Anhang zu finden. 3.3 DAS BRUMMEN MUSS WEG: DAS GLEICHRICHTER-PROBLEM Das Gleichrichter-Problem eignet sich gut für problemorientierten Unterricht. Die Schüler sollen dabei möglichst selbstständig von einer sinusförmigen Wechselspannung zu einer gut geglätteten Gleichspannung gelangen. Die jeweiligen Zwischenschritte auf dem Weg dahin, also die veränderten Spannungsverläufe, werden durch einen Lautsprecher sowohl hörbar sowie durch einen Oszillosgraphen auch sichtbar gemacht. Wegen des Oszillosgraphen eignet sich der Versuch eher für ein Praktikum in Stationen. Eine mögliche Implementierung im Unterricht wird auf dem Aufgabenzettel im Anhang vorgeschlagen. 3.4 EINE INTELLEKTUELLE HERAUSFORDERUNG: DER ASTABILE MULTIVIBRATOR Der astabile Multivibrator, auch astabile Kippstufe genannt, ist ein Beispiel für Transistoren als integrierte Schalter, wobei sich zwei Transistoren gegenseitig ein- und ausschalten. Ein Versuchsaufbau sowie eine Versuchsanleitung für Schüler ist im Anhang zu finden. Neben dem tollen Blinkeffekt werden diese Kippstufen vor allem zur Erzeugung von periodischen Rechtecksignalen verwendet, die als Taktgeber für verschiedene Prozesse dienen können. Diese Rechteckspannung wird über Kollektor und Emitter eines Transistors abgegriffen. Neben der astabilen Kippstufe gibt es auch stabile Varianten, wo die anliegende Spannung an einem Transistor (bzw. am entsprechenden Kondensator) nicht automatisch durch den anderen Transistor genullt, sondern gespeichert wird. Diese Flip Flops sind grundlegende Elemente der Rechentechnik. Die Erklärung des Versuchs gelingt dann besonders gut, wenn der Lehrer im Rahmen der Elektrodynamik nicht nur von Spannungen, sondern auch von Potentialen gesprochen hat. Nur so ist es relativ einfach zu erklären, dass der Kondensator, der gerade geladen wird, der Basis des gegenüberliegenden Transistors das Potential entzieht, sodass über die Basis kein Strom mehr fließen kann und der Transistor damit sperrt. 3.3 Das Brummen muss weg: Das Gleichrichter-Problem 29 3.5 FUNKTIONSPRINZIP EINER STABILISIERTEN SPANNUNGSQUELLE Ähnlich wie das Gleichrichterproblem eignet sich auch die Suche nach stabilisierten Spannungsquellen für problemorientierten Unterricht. Dabei verwendet man ein (nicht stabilisiertes) Netzgerät und ein Potentiometer, um die Spannung für ein einfaches Radio so einzustellen, damit es betrieben werden kann. Über dem Radio wird die Spannung gemessen. Ändert man nun die Lautstärke, so verändert sich auf Grund von Widerstandsänderungen auch die über dem Radio abfallende Spannung. Das kann zum Ausfall oder gar zum Defekt des Radios führen. Abhilfe kann eine einfache Transistorschaltung schaffen. Im Anhang ist ein Aufgabenblatt zu finden, das diesen Versuch darstellt. Statt eines Radios wurde eine Glühlampe mit Schalter verwendet. Ist der Schalter geöffnet, so fließt zwar kein Strom, über dem „Gerät“ Lampe mit Schalter liegt aber dennoch die vorläufige Betriebsspannung (Leerlaufspannung) an. Wird der Schalter geschlossen, sinkt die über der Lampe und dem Schalter abfallende Spannung stark ab. Mit der angegebenen Transistorschaltung wird dieses Absinken zwar nicht gänzlich verhindert, aber dennoch abgemildert. Als Zusätz könnte man den Schülern die (freiwillige) Aufgabe geben, sich über Verbesserungen dieses Verfahrens zu informieren. Diese Zusatzaufgabe könnte somit als kleiner Anstoß für interessierte Schüler sein, die sich damit in eine intrinsische Motivation hineinsteigern können. 30 Kapitel 3 Experimente 4 LITERATUR Dorn-Bader: „Physik – Oberstufe Gesamtband 12/13“ (1986, Schroedel) Joachim Grehn et al.: „Metzler Physik“ (1998, Schroedel) Ernst W. Otten: „Repetitorium Experimentalphysik“ (2003, Springer) Datenblatt MOSFET BUZ 11: http://www.produktinfo.conrad.com/datenblaetter/150000-174999/151334-da-01-en-BUZ11_MOSFET.pdf (Letzter Zugriff: 07.07.2010) 32 Kapitel 4 Literatur 5 ANHANG – ARBEITSBLÄTTER Achtung: Online-Version! Anhänge als Word-Dokumente Das Gleichrichter-Problem.docx Der astabile Multivibrator.docx Funktionsprinzip einer stabilisierten Spannungsquelle.docx Kennlinien einer Halbleiterdiode.docx 34 Kapitel 5 Anhang – Arbeitsblätter