Gruppengeschwindigkeit: Spezielle Lösung der Wellengleichung

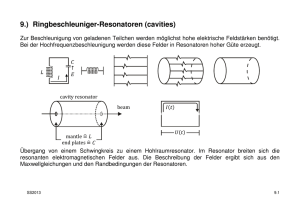
Wiederholung
Mit dieser Geschwindigkeit
Gruppengeschwindigkeit:
wird die Energie
Spezielle Lösung der Wellengleichung:
transportiert!
Lineare Überlagerung!
spezieller für t=0
Es gilt
Endlicher Wellenzug:
k0
k
x
Ist A(k) relativ eng um k0 konzentriert
das ist aber u(x',0)
mit
Zum
Vergleich:
Gruppengeschwindigkeit
gilt immer!
10.11. Hohlraumresonator
Der Grenzfall eines Kondensators bei sehr hohen Frequenzen
(Fläche umrandet von
Magnetfeld im Kondensator
Die ''Kapazität'' ist
nicht mehr
Faraday:
Fläche umrandet von
zusätzlicher Beitrag
Aufspaltung in zwei Teile
(Korrektur durch das B-Feld)
für r=0 (Im Zentrum
des Kondensators)
E ist die 1. Näherung
ändert auch
………
Besselfunktion:
(Immer Lösungsansatz bei Zylindersymmetrie)
Bei noch höherer Frequenz: bei
B sieht entsprechend so aus:
Hohlraumresonator:
bei r=a kann auch eine leitende Wand
angebracht
werden!
Hochfrequenzkreis mit Resonator:
Q=Güte des
Resonators bis
10
bei supraleitenden
Hohlraumresonatoren!
10.12 Ausbreitung von Wellen im Rechteckhohlleiter
An den Stellen, an denen E=0, kann man Metallplatten anbringen
Wellenleiter!
Wellenlänge ohne,
Wellenlänge im Hohlleiter
da
nur Ausbreitung wenn
Schönes Beispiel für Phasengeschwindigkeit:
immer
z sei Ausbreitungsrichtung
für
und
damit