Klausur Analyse elektr. Schaltgn. SS 13 am 18.07.2013 Prof. H

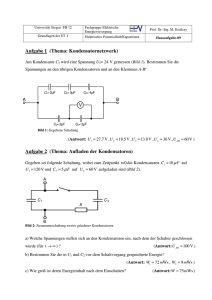
Klausur Analyse elektr. Schaltgn. SS 13 am 18.07.2013 Prof. H. Edlich S.- 1 Bitte Ankreuzen !!!!
Letzter Versuch ( dritter Gesamtversuch )?
Ja
Nein
Name, Vorname __________________________________
EDV-Nr.
__________________________________
__________________________________
Beurteilung
Der Austausch von Unterlagen zwischen den Kandidaten während der Klausur ist nicht
gestattet. Ergebnisse werden nur bewertet, wenn alle Zwischenrechnungen auch bei
Matrizen aufgeführt sind. Bitte tintenfesten Stift verwenden ! Der Gebrauch von Handys,
PAD’s, Laptops, Bluetooth, WLAN oder aller dem Betrug dienenden Mittel ist nicht
gestattet !! Es wird nicht gesprochen !
1. Aufgabe ( Netzwerke)
Iq2
In nebenstehender Schaltung (Bild 1) sind Uq1, Iq2,
R3 und IL gegeben. Gesucht ist die Spannung UL
und der Lastwiderstand RL
1.1 als Funktion der allgemeinen obigen Werte,
Uq1
1.2 für die Werte Uq1 = 5V, Iq2 = 2 mA,
Ω, IL = 1 mA.
R3 = 1kΩ
1.3 Begründen Sie bitte, warum Sie diese Berechnungsmethode gewählt haben und welche
anderen Berechnungsverfahren für diese Schaltung existieren.
R3
RL
UL
ΙL
Bild 1
2. Aufgabe (Elektrostatik)
Gegeben sind zwei Kondensatoren mit nebenstehenden Kapazitäten C, den Isolationswiderständen Ris und den Nennspannungen
UN = 1000V (Bild 2).
2.1 Parallelschaltung der Kondensatoren
Berechnen Sie bitte die Gesamtkapazität Cges1
der Kondensatoren, den gesamten
Isolationswiderstand Risges1 und die zulässige
Gesamtspannung Uges1 der Parallelschaltung.
C1 =
600µ
µF
C2 =
800µ
µF
Ris1 =
2 MΩ
Ω
Ris2 =
3 MΩ
Ω
Bild 2
2.2 Reihenschaltung der Kondensatoren
Welche Maßnahmen sind erforderlich, um für Gleichspannung die gleiche Spannung UN an
den Kondensatoren zu erzielen, wobei die Nennspannung nicht überschritten werden soll?
Berechnen Sie die dazu erforderlichen Bauelemente. Wie groß ist die Gesamtkapazität
Cges2 der Kondensatoren, der gesamter Isolationswiderstand Risges2 mit
Zusatzbauelementen und die zulässige Gesamtspannung Uges2 der Parallelschaltung?
2.3 Welchen Scheinwiderstand (Impedanz) Z hat C1 für die Frequenz f = 50 Hz ? Sind die
Isolationswiderstände bei diesen oder höheren Frequenzen zu beachten?
WordXP/Klausuren_Weingarten/Klaus2013_2013_WS_AN_Sem
HS Weingarten-Rav. FB ET u. IF
Analyse el. Schaltgn. Prof. H. Edlich S.- 1 -
Klausur Analyse elektr. Schaltgn. SS 13 am 18.07.2013 Prof. H. Edlich S.- 2 3. Aufgabe (Magnetostatik)
Ein Kleinrelais besteht im Prinzip aus einem U-förmigen
Kleinrelais
Eisenkern mit einer Spule und einem beweglichen
Anker (Bild 3). Der Anker wird ohne Strom durch eine
Feder vom Kern weggedrückt (Relais abgefallen), mit
Strom bewegt sich der Anker zum Kern und betätigt die
Kontakte (Relais angezogen).
Kern
Spule:
Strom
Ι = 50 mA,
Windungszahl
N = 1000 Wdgn.
Fläche von Eisen u. Luftspalt:
A = 25,13 mm2
Magnetische Widerstände RM: E = Eisen, L = Luft
Spule
6
Ι
Kern einschließich Anker :
RME = 3,979*10 1/H
Ι
7
Luftspalt :
RML = 3,5811*10 1/H
Der Luftspalt am Drehpunkt B des Ankers wird vernachlässigt.
3.1 Berechnen Sie bitte die magnetische Spannung (oder Durchflutung) die
Spulenstrom entsteht. Ist die magnetische Spannung meßbar ?
Luftspalt
Anker
Drehpunkt
B des
Ankers
Bild 3
durch den
3.2 Abgefallener Zustand des Relais
Berechnen Sie den Gesamtfluß ΦEL und die Flußdichte BEL im magn. Kreis sowie die
Kraft FEL auf den Anker anhand der Formel FEL = (A*BEL2) / (2*µ
µo), (A = Fläche des
Luftspaltes).
3.3 Angezogener Zustand des Relais
Berechnen Sie den Gesamtfluß ΦE und die Flußdichte BE im magn. Kreis sowie die Kraft
FE auf den Anker anhand der Formel FE = (A*BE2) / (2*µ
µo),
3.4 Angezogener Zustand des Relais, Stromabschaltung
Nach dem Abschalten des Stromes entsteht durch die Restmagnetisierung (Remanenz) ein
Restfeld BR und eine Kraft FR, die den Anker am Kern halten will. Berechnen Sie die
zulässige Größe der Remanenz BR, wenn die die Remanenzkraft FR = 0,2*FEL sein soll.
Welche Wert hat sinnvollerweise die Gegenkraft FG der Feder, die den Anker wieder
abfallen läßt?
4. Aufgabe (Übertragungsfunktionen)
Gegeben ist nebenstehende Schaltung (Bild 4).
4.1 Berechnen Sie bitte in allgemeiner Form die
Übertragungsfunktion H und Dämpfungsfunktion D als
Funktion der zunächst unbekannten Bauelemente R, L, C und
der Frequenz. Welche Filterart und Ordnung liegt vor ? Geben
Sie die Normalform des Filters sowie die Werte Ho, a1, b1 an.
4.2 Berechnen Sie das Dämpfungsmaß a/dB für die Frequenz
f = 20 kHz sowie L = 10 mH, R = 888,6 Ω,
C = 6,3325 nF.
L
U1
C
R U2
Bild 4
4.3 Welche Bedeutung hat die Grenzfrequenz und welchen
Dämpfungswert hat sie in der Regel ?
Viel Erfolg!
WordXP/Klausuren_Weingarten/Klaus2013_2013_WS_AN_Sem
HS Weingarten-Rav. FB ET u. IF
Analyse el. Schaltgn. Prof. H. Edlich S.- 2 -
Klausur Analyse elektr. Schaltgn. SS 13 am 18.07.2013 Prof. H. Edlich S.- 3 Lösungen:
1. Aufgabe
1.1 UL = Uq1 – R3*(Ιq2 + ΙL)
1.2 UL = 2V, RL = 2kΩ.
1.3 Es sind fast alle anderen Verfahren möglich.
2. Aufgabe
2.1 Cges = 1 400 µF, Rges = 1,2 MΩ, Uges = 1000 V.
2.2 Cges = 342,86 µF, R2zus = 6 MΩ, Rges = 4 MΩ, Uges = 2000 V !
2.3 ZC = - j*5,305Ω.
3. Aufgabe
3.1
3.2
3.3
3.4
4. Aufgabe
4.1 D = 1 + P*ωg*L/R + P2*ωg2*L*C, Ho = 1, a1 = ωg*L/R, b1 = ωg2*L*C,
4.2 a(20 kHz) = 3,0103 dB,
4,3 Die Grenzfrequenz fg trennt den Durchlaßbereich vom Sperrbereich bei
allen Filterarten und hat in Regel den Dämpfungswert a ≈ 3 dB.
UM = Θ = 50 A,
FEL = 0,025 N
FE = 2,5 N
FR = 0,005 N
BR = 0,02236 Tesla
Federkraft Fg FEL > Fg > FR z.B. Fg = 0,01 N.
Word/Klausuren/Klausur_2013_2013_SS_AN_Sem+Loes
Edlich
 6. 05. 2013
Prof. H.
WordXP/Klausuren_Weingarten/Klaus2013_2013_WS_AN_Sem
HS Weingarten-Rav. FB ET u. IF
Analyse el. Schaltgn. Prof. H. Edlich S.- 3 -