Lösungen Aufgaben 37.38.39

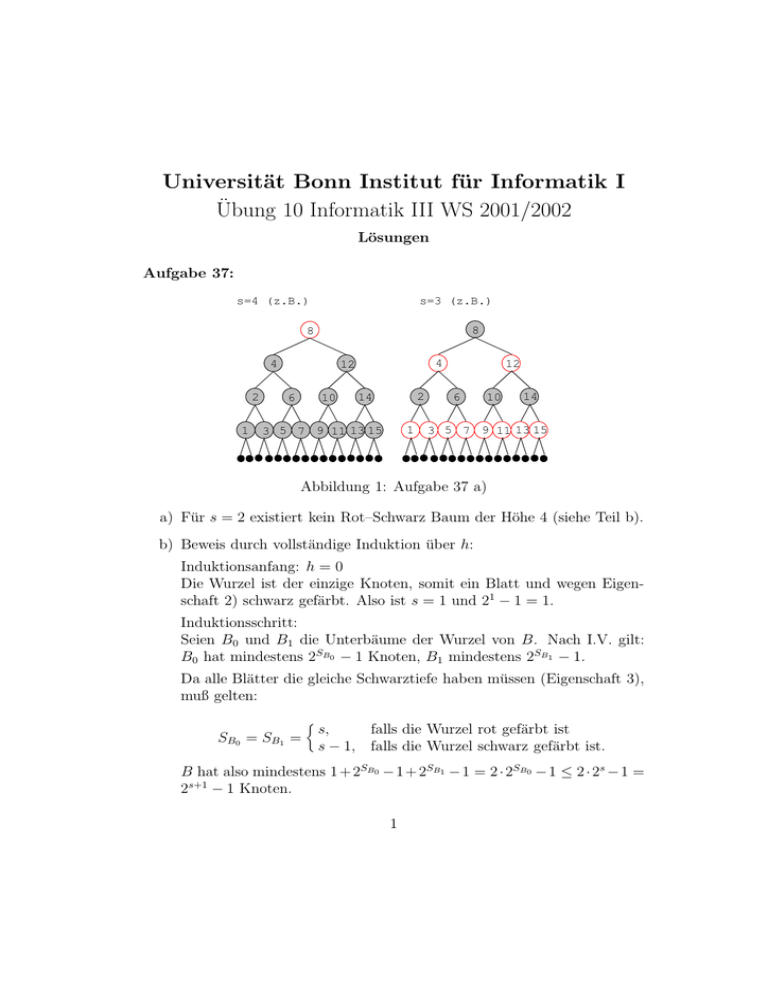
Universität Bonn Institut für Informatik I
Übung 10 Informatik III WS 2001/2002
Lösungen
Aufgabe 37:
s=4 (z.B.)
s=3 (z.B.)
8
8
4
2
1
4
12
6
10
2
14
1
3 5 7 9 11 13 15
12
6
10
14
3 5 7 9 11 13 15
Abbildung 1: Aufgabe 37 a)
a) Für s = 2 existiert kein Rot–Schwarz Baum der Höhe 4 (siehe Teil b).
b) Beweis durch vollständige Induktion über h:
Induktionsanfang: h = 0
Die Wurzel ist der einzige Knoten, somit ein Blatt und wegen Eigenschaft 2) schwarz gefärbt. Also ist s = 1 und 21 − 1 = 1.
Induktionsschritt:
Seien B0 und B1 die Unterbäume der Wurzel von B. Nach I.V. gilt:
B0 hat mindestens 2SB0 − 1 Knoten, B1 mindestens 2SB1 − 1.
Da alle Blätter die gleiche Schwarztiefe haben müssen (Eigenschaft 3),
muß gelten:
SB0 = SB1 =
s,
falls die Wurzel rot gefärbt ist
s − 1, falls die Wurzel schwarz gefärbt ist.
B hat also mindestens 1 + 2SB0 − 1 + 2SB1 − 1 = 2 · 2SB0 − 1 ≤ 2 · 2s − 1 =
2s+1 − 1 Knoten.
1
c) Da auf einem Pfad zwischen Wurzel und Blatt nie zwei rote Knoten
aufeinander folgen (Eigenschaft 4), muß auf einem maximalem Pfad
mindestens die Hälfte aller Knoten schwarz sein, es gilt also
s≥
h+1
.
2
Es gilt also h ≤ 2s − 1, die maximale Anzahl an Knoten wird für
h = 2s−1 erreicht. Aus Aufgabe 34b) wissen wir, daß in einem binären
der Baum der Höhe 2s − 1 die maximale Anzahl von Knoten 22s − 1
ist.
Aufgabe 38 a):
a) Siehe Abbildung 2
b) Nein!
Bezeichne A(k) die minimale Anzahl von Knoten eines AVL–Baumes
der Höhe k. Offensichtlich gilt: A(0) = 1 und A(1) = 2. Für k ≥ 2
muß ein AVL–Baum der Höhe k eine Wurzel haben, und ein Teilbaum
muß Höhe k − 1 haben — damit mindestens A(k − 1) Knoten —,
der andere Teilbaum mindestens die Höhe k − 2 und damit mindestens
A(k−2). Andererseits können wir auch einen AVL–Baum konstruieren,
indem wir als Teilbäume AVL–Bäume der Höhen k − 2 und k − 1 mit
minimaler Knotenzahl benutzen. Es folgt für k ≥ 2:
A(k) = 1 + A(k − 1) + A(k − 2).
Dies läßt sich auch mit Hilfe der Fibonacci–Zahlen1 ausdrücken:
A(k) = Fk+3 − 1.
Das läßt sich durch Induktion über k zeigen:
A(0) = 1 = F3 − 1
A(1) = 2 = F4 − 1
A(k) = 1+A(k −1)+A(k −2) =(I.A.) 1+Fk+2 −1+Fk+1 −1 = Fk+3 −1
Somit gilt A(9) = F12 − 1 = 143 > 100 ⇒ ein AVL–Baum der Höhe 9
mit 100 Knoten existiert nicht.
2
Aufgabe 39:
Sei ein halb-balancierter binärer Baum T der Höhe h ≥ 1 mit n Blättern
gegeben. Der kürzeste Pfad von der Wurzel von T zu einem Blatt hat mindestens die Länge h/2 falls h gerade ist und mindestens die Länge (h + 1)/2
falls h ungerade ist, das folgt direkt aus der Halb-Balancierung von T .
Ein vollständiger Baum der Höhe x hat 2x Blätter, unser bei Höhe h/2 bzw.
(h + 1)/2 abgeschnittene Baum hat also 2h/2 bzw. 2(h+1)/2 Blätter, unser
Baum T hat jedenfalls mindestens so viele Blätter.
n ≥ 2h/2
⇐⇒
h ≤ 2 log n
Diese Abschätzung läßt sich geringfügig weiter verbessern, wenn man noch
genauer die Blätter von T zählt, die alle nötig sind, damit T wirklich die
Höhe h erreicht; alle Teilbäume von T sind auch halbbalanciert.
1
mit F0 = 0, F1 = 1.
3
4