Schwingungsspektroskopie
Werbung

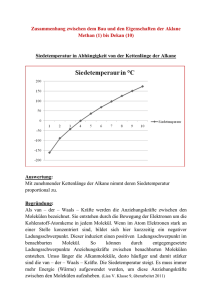
Schwingungsspektroskopie • In N-atomigen Molekülen haben wir 3N-5 (linear) bzw. 3N-6 (nichtlinear) Freiheitsgrade der Schwingung, welche die Position der Atome relativ zueinander beschreiben. Der Potentialterm wird zu einer komplizierten Matrix, da jede Auslenkung eines Atoms im Prinzip die Kraft auf alle anderen beeinflusst. Man kann jedoch einen Satz von Koordinaten finden, welche die Matrix der potentiellen Energie diagonalisieren. Diese heißen Normalkoordinaten (-schwingungen oder – moden), und stellen eine Überlagerung von Bewegungen aller Atome dar. • Jede Normalschwingung kann als unabhängiger harmonischer Oszillator mit einer Eigenfrequenz ωi verstanden werden. Die Schwingungsenergie des Moleküls ergibt sich als Summe der Energien der unabhängigen Oszillatoren. Schwingungsspektroskopie • Die Normalschwingungen eines dreiatomigen Moleküls sind die symmetrische und asymmetrische Streckschwingung, sowie die Biegeschwingung. Streckschwingungen haben höhere Frequenzen als Biegeschwingungen, die asymmetrische i.a. eine höhere Frequenz als die symmetrische • Die Anregung einer Normalschwingung ist erlaubt, wenn sich das Dipolmoment entlang der Normalkoordinate wahrend der Schwingung verändert. • Die symmetrische Streckschwingung des CO2 ist daher IR-inaktiv. Im H2O tauchen dagegen alle Schwingungen im IR-Spektrum auf. •Wird die Anharmonizität einbezogen treten auch Obertöne und Kombinationsbanden auf. Schwingungsspektroskopie •Oft sind bestimmte Kraftkonstanten zwischen zwei Atomen groß und auch in verschiedenen Molekülen sehr ähnlich. Dies führt zum Konzept der Gruppenschwingung und ermöglicht die Identifikation funktioneller Gruppen. Die folgende Tabelle zeigt einige Beispiele: Wellenzahl /cm-1 Funktionelle Gruppe 3600 -O-H 3400 -N-H, -NH2 (zwei Banden) 3300 C H 2900-3000 -CH3, -CH2 2800 CO-H (Aldehyd, zwei Banden) 1750 -C=O 1650 -C=C- 1500/1600 Benzolring 700 C-Cl Schwingungsspektroskopie • Fourier-Transform Spektroskopie beruht darauf, dass Zeit- und Frequenzdomäne äquivalent sind. Das Spektrum wird in der Zeitdomäne beobachtet und die beteiligten Frequenzen durch Fourier-Transformation gewonnen. In Analogie zur Musik wird ein ganzer „Akkord“ aufgenommen und in seine einzelnen „Töne“ zerlegt. • Im IR werden daher Fourier-IR Spektrometer (FT-IR) verwendet, deren zentrales Element ein Michelson-Interferometer ist. Seine Vorteile liegen in der schnelleren Aufnahme von Spektren, dem besseren Signal/Rausch Verhältnis und der Möglichkeit, niederfrequente Schwingungen (< 400 cm-1) zu beobachten. Ramanspektroskopie • Eine Alternative in der Schwingungsspektroskopie bietet der Raman-Effekt, die inelastische Streuung von Licht an Molekülen. Der Raman-Effekt beruht auf dem durch die Strahlung induzierten Dipolmoment. Dieses ist proportional zur molekularen Polarisierbarkeit, die ein Maß für die Verschiebbarkeit positiver und negativer Ladungen relativ zueinander darstellt. • Zusätzlich zum elastisch gestreuten Primärlicht (Rayleigh-Linie) treten noch die Stokes- und Anti-Stokes-Linien auf, deren Frequenzverschiebung einem Schwingungsübergang entspricht. Stokes Anti-Stokes ν0-∆ν ν0 ν0+∆ν v=1 v=0 Stokes Anti-Stokes Ramanspektroskopie • Bedingung für Raman-Aktivität ist eine sich während der Schwingung ändernde Polarisierbarkeit. Diese Bedingung ist für alle zweiatomigen Moleküle, auch homonukleare, erfüllt, sowie für viele IR-inaktive Banden in mehratomigen Molekülen. Infrarot- und Raman-Spektroskopie ergänzen sich daher hervorragend. • Für die Intensität des Streulichts gilt I Streu = 1 λ 4 daher ist eine Anregung im Vis bzw. UV Bereich vorteilhaft. • Die Vorteile der Raman-Spektroskopie bestehen a) in der Möglichkeit IRverbotene Banden zu beobachten, b) der Detektion im sichtbaren Spektralbereich, c) der leichten Kombination mit Mikroskopie und d) der Tatsache, dass Wasser ein schwacher Raman-Streuer ist. Die Raman-Spektroskopie erfordert eine intensive, schmalbandige Lichtquelle (Laser) zur Anregung sowie eine gute Unterdrückung der Anregungsfrequenz IR- vs. Ramanspektroskopie „Alternativverbot“ in Molekülen mit Inversionszentrum CS2 Infrarotspektrum Ramanspektrum Frank-M. Schnepel, Chemie in unserer Zeit, 13, S. 33 (1979) Klausuranmeldung Di, 24. Juni 18 Uhr, HS A TecFun & LA Gym Elektronische Prüfungsanmeldung mit sb@home http://www.uniwuerzburg.de/fuer/studierene/online-service/ Teilmodul: Physikalische Chemie II (Grundlagen der Quantenmechanik und Spektroskopie) für Studierende der Ingenieurwissenschaften Kurzbezeichnung 08-IPC2; TM-Nr:300025 eingetragen : Semester : 20081 Prüfer : Fischer Prüfungsdatum : 24.06.2008 Uhrzeit : 18:00 Uhr Beginn Anmeldung : 02.06.2008 Ende Anmeldung : 20.06.2008 Ende Rücktritt : 20.06.2008 TecFun-Scheine Scheine IPC1, WS 2007/08 können täglich zwischen 8 und 11 Uhr bei Frau König im Sekretariat Physikalische Chemie, 2. Stock abgeholt werden Bescheinigung Herr Vorname Nachname Matrikelnummer 11111111 hat im Wintersemester 2007/08 an dem Teilmodul Physikalische Chemie 1 für Ingenieure (IPC 1 und IPC 2) mit Erfolg teilgenommen. Die Veranstaltung entspricht 6 ECTS Punkten Die Teilmodulprüfung wurde mit der Note bewertet Teilchen auf dem Ring Behandlung in Polarkoordinaten r und φ Hamilton-Operator: Wellenfunktion: Φ = Aml ⋅ eimlφ Energie: ml2 ⋅ h 2 E= 2I Drehimpuls: ml=±2 ml=±1 ml=0 2 2 − h ∂ Hˆ = 2 I ∂φ 2 Lz = ml ⋅ h • Rotationsenergie ist quantisiert • Abstände zwischen Energieniveaus nehmen zu mit ml • ml –Entartung Teilchen auf dem Ring Wellenfunktionen 2π ⋅ r λ= ml ml=0: Wellenfunktion hat überall die gleiche Amplitude, Aufenthaltswahrscheinlichkeit ist überall gleich, Teilchen ist komplett delokalisiert. Daher darf der Impuls genau bestimmt sein, ohne die Unschärferelation zu verletzen.