Bäume (Nachtrag) - johner.org: Home

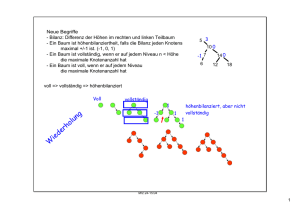
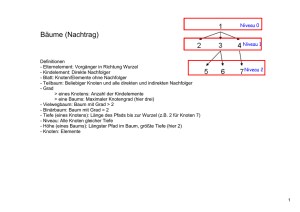
SOTE1­2016­04­04.notebook
Bäume (Nachtrag)
Definition
• Elternelement: Direkter Vorgänger (Richtung Wurzel)
• Kindelement: Direkte Nachfolger
• Blatt: Alle Knoten ohne Kindelemente
• Teilbaum: Beliebiges Element im Baum mit allen direkten und indirekten Nachfolgern
• Grad
> eines Knotens: Anzahl der direkten Nachfolger
> eines Baums: Maximaler Knotengrad (hier: 3)
• Vielwegbaum: Baum mit Grad > 2
• Binärbaum: Baum mit Grad 2
• Tiefe eines Knotens: Länge des Pfads zur Wurzel z.B. 7 hat Tiefe 2
• Niveau: Alle Knoten gleicher Tiefe
• Höhe (eines Baums): Größte Tiefe, längster Pfad (hier 2)
April 04, 2016
Niveau 0
Niveau 2
1
SOTE1­2016­04­04.notebook
April 04, 2016
Binäre Suchbäume
Baum des Grads 2, bei denen sich im linken Teilbaum kleinere und im rechten Teilbaum größere Elemente befinden.
2
SOTE1­2016­04­04.notebook
April 04, 2016
Elemente in einen binären Suchbaum einsortieren
a) 10, 5, 14, 7, 18, 12, 6
10
14
5
7 12 18
6
c) 5, 6,7, 10, 12, 14, 18
5
6
7
10
12
14
b) 5, 10, 7, 14, 12, 18, 6
5
10
14
7
6
18
12
18
ein zu einer linearen Liste entarteter Suchbaum
3
SOTE1­2016­04­04.notebook
April 04, 2016
Begriffe
• Bilanz : Differenz der Höhen im rechten und linken teilbaum
• Höhenbilanzierter Baum : Baum, bei dem jeder Knoten die Bilanz 0, 1 oder ­1 hat
• Vollständiger Baum : Baum, der auf jedem Niveau n < Höhe die maximale Knotenanzahl hat (auf jedem Niveau außer dem "untersten")
­1
10
• Voller Baum : Baum, der auf jedem Niveau die maximale Knotenanzahl hat
14 0
2 5
18
­1 7 12
0
6
Voll ­­> Vollständig ­­> höhenbilanziert
0
1
1
1
1
­1
1 Nicht vollständig, da hier Knoten fehlt
2
4
SOTE1­2016­04­04.notebook
April 04, 2016
AVL­Bäume
­ Adelson, Veliskii und Landis
­ höhenbilanzierte binäre Suchbäume
Rezept / Algorithmus zum Einfügen von Elementen in binären Suchbäumen
1. Element einfügen wie bisher
2. Sofort auf Höhenbilanziertheit prüfen
3. Falls die Balance (B) < ­1 oder > +1, sofort umstrukturieren
1. Linksrotation falls B > 1
2. Rechtsrotation, falls B < ­1 3. Rechts­Links­Rotation, falls B > 1 und B(Nachfolgers) ­1
4. Links­Rechts­Rotation, falls B < ­1 und B(Nachfolgers) +1
5
SOTE1­2016­04­04.notebook
April 04, 2016
m
f
f
f
o
a
h
m
a
c
c
m
a
h
o
c
h
o
Regel für Rechts/Linksrotation
Falls ein Knoten nicht höhenbilanziert ist (hier m), wird er nach rechts/links geschoben.
Ein möglicher rechter/linker Nachfolger (hier h) wird linker/rechter Nachfolger des rotierten Knotens (m)
6
SOTE1­2016­04­04.notebook
April 04, 2016
Aufgabe: 5­8­2­6­10­9
2
5
2
8
81
6
10 ­1
5
2
6 9
10
9
Ein möglicher rechter/linker Nachfolger (hier h) wird linker/rechter Nachfolger des rotierten Knotens (m)
7
SOTE1­2016­04­04.notebook
April 04, 2016
­2
1
0
­1
5
2
1
5
5
7
4
2
4
3
1
3
7
4
7
2
1
3
1. Teilschritt: Linksrotation
5
4
4
7
2
1
3
5
2
1
3
1, 7, 3, 4, 2, 6, 5
7
2. Teilschritt: Rechtsrotation (um "Problemknoten")
8
SOTE1­2016­04­04.notebook
April 04, 2016
1, 7, 3, 4, 2, 6, 5
2
1
1
7 ­1
3
3
3
7 ­2
1
7
2
1
3
3
41
6
7
1
2
6
4
1
1
6
2
­1
4+1
5
7
9