Vorlesungsmitschrieb

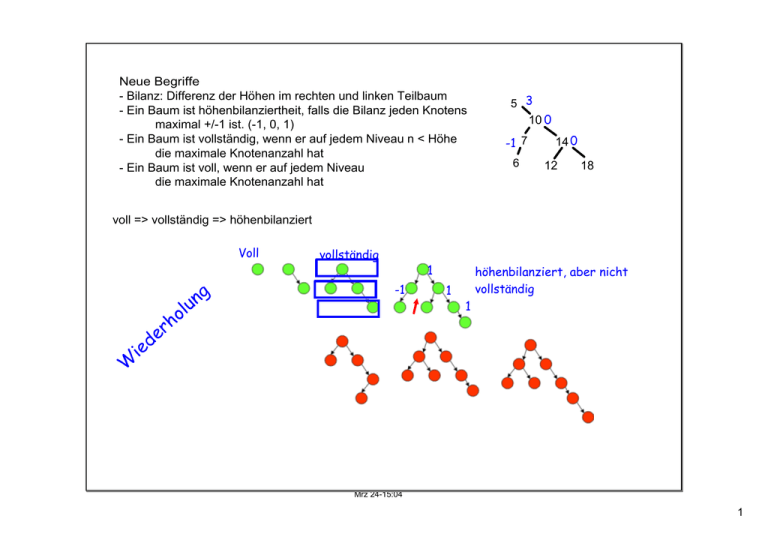
Neue Begriffe
­ Bilanz: Differenz der Höhen im rechten und linken Teilbaum
­ Ein Baum ist höhenbilanziertheit, falls die Bilanz jeden Knotens maximal +/­1 ist. (­1, 0, 1)
­ Ein Baum ist vollständig, wenn er auf jedem Niveau n < Höhe
die maximale Knotenanzahl hat
­ Ein Baum ist voll, wenn er auf jedem Niveau die maximale Knotenanzahl hat
5 3
10 0
-1 7
6
14 0
12
18
voll => vollständig => höhenbilanziert
Voll
vollständig
1
g
n
u
e
d
e
-1
ol
h
r
höhenbilanziert, aber nicht
vollständig
1
1
i
W
Mrz 24­15:04
1
AVL­ Bäume
­ Adelson­ Velskii­ Landis
­ höhenbilanzierte binäre Suchbäume
Nächste Stunde: Rezept zum Einfügen von Elementen, dass der Baum höhenbilanzert bleibt.
Rezept (Algorithmus) zum Einfügen von Elementen in AVL­Bäume
1) Einfügen wie bisher
2) Sofort auf Höhenbilanziertheit prüfen
3) Falls nicht höhenbilanziert (die Balance < ­1 oder > +1), dann sofort umstrukturieren:
a) Linksrotation, falls B > 1
b) Rechtsrotation, falls B < ­1 c) Rechtlinksrotation, falls B > 1 und B(Nachfolger) ­1 d) Linksrechtsrotation, falls B < ­1 und B(Nachfolger) +1 Mrz 24­15:11
2
Regel für Rechts­/Linksrotation:
Falls ein Knoten nicht höhenbilanziert ist (hier M), wird er nach rechts/links geschoben. Ein möglicher rechter/linker Nachfolger (H) wird linker/rechter Nachfolger des rotierten Knotens (hier M).
M
F
F
F
M
H
O
A
A
M
A
O
H
C
C
H
O
C
5­8­2­6­10­9
Mrz 31­14:07
3
Rezept (Algorithmus) zum Einfügen von Elementen in AVL­Bäume
1) Einfügen wie bisher
2) Sofort auf Höhenbilanziertheit prüfen
3) Falls nicht höhenbilanziert (die Balance < ­1 oder > +1), dann sofort umstrukturieren:
a) Linksrotation, falls B > 1
b) Rechtsrotation, falls B < ­1 c) Rechtlinksrotation, falls B > 1 und B(Nachfolger) ­1 d) Linksrechtsrotation, falls B < ­1 und B(Nachfolger) +1 Regel für Rechts­/Linksrotation:
Falls ein Knoten nicht höhenbilanziert ist (hier 5), wird er nach rechts/links geschoben. Ein möglicher rechter/linker Nachfolger (6) wird linker/rechter Nachfolger des rotierten Knotens (hier 5).
5­8­2­6­10­9
8
5 3-1=2
0 2
8
6
5
2-1=1
10
8
2
05
6
10
9
2
6
0
10 -1
9
0-1=-1
9
Mrz 31­14:14
4
c) Rechtlinksrotation, falls B > 1 und B(Nachfolger) ­1 d) Linksrechtsrotation, falls B < ­1 und B(Nachfolger) +1 5
-2
1
5
5
0
4
4
2
7
7
7
2
2 3
1
1
4
3
1
3
1. Teilschritt: Links-Rotation
5
4
1, 7, 3, 4, 2, 6, 5
4
7
5
2
2
7
1
3
1
3
2. Teilschritt: Rechts-Rotation
Mrz 31­14:32
5
c) Rechtlinksrotation, falls B > 1 und B(Nachfolger) ­1 d) Linksrechtsrotation, falls B < ­1 und B(Nachfolger) +1 1, 7, 3, 4, 2, 6, 5
1 2
1
7 -1
3 1
3
3
1
7
7 -1
1
7
3
3 0
4
7 -1
1
2
4
Recht-Links-Rotation
3 1
3
7 -2
1
2
41
6
3 1
7
1
2
6
4
6 -1
1 1
2
4
1
5
7
höhenbilanzierter, aber nicht
vollständiger und nicht voller Baum
Links-Rechts-Rotation
Mrz 31­14:49
6
Nachtrag zu binären Suchbäumen (nicht speziell für AVL­Bäume)
Löschen von Elementen
3
1. Fall: Zu löschender Knoten ist ein Blatt: einfach Blatt löschen. Bsp: Knoten 2
6
1
2
7
5
2. Fall: Zu löschener Knoten hat ein Kindelement z.B. 4: Kindelement des zu löschenden Knotens (hier 5) direkt mit dem Elternelement des zu löschenden Knotens (hier 6) verbinden
3. Fall: Zu löschender Knoten hat zwei Kindelemente z.B. 3: Element mit dem größten Element des linken (2) bzw. kleinsten Element des rechten Teilbaums (4)
ersetzen.
Bei AVL­Bäumen müsste zusätzlich die Höhenbilanziertheit wieder hergestellt werden.
Lösungen zu Übungsaufgaben selbst prüfen z.B. mit
http://alfi.ira.uka.de/lehre/sommer2002/AVLTreeApplet/avl.html
sonst suchen nach AVL Baum Applet
Mrz 31­15:03
7