Selbstgeführte Wechselrichter - antriebstechnik.fh

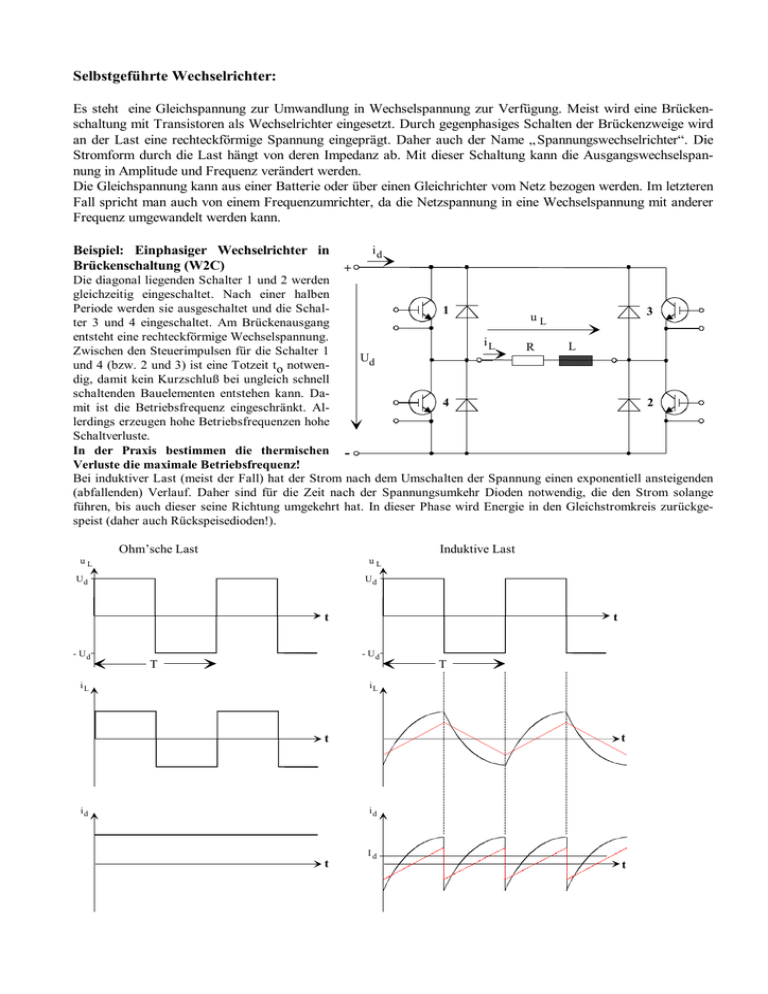
Selbstgeführte Wechselrichter:
Es steht eine Gleichspannung zur Umwandlung in Wechselspannung zur Verfügung. Meist wird eine Brückenschaltung mit Transistoren als Wechselrichter eingesetzt. Durch gegenphasiges Schalten der Brückenzweige wird
an der Last eine rechteckförmige Spannung eingeprägt. Daher auch der Name „Spannungswechselrichter“. Die
Stromform durch die Last hängt von deren Impedanz ab. Mit dieser Schaltung kann die Ausgangswechselspannung in Amplitude und Frequenz verändert werden.
Die Gleichspannung kann aus einer Batterie oder über einen Gleichrichter vom Netz bezogen werden. Im letzteren
Fall spricht man auch von einem Frequenzumrichter, da die Netzspannung in eine Wechselspannung mit anderer
Frequenz umgewandelt werden kann.
Beispiel: Einphasiger Wechselrichter in
Brückenschaltung (W2C)
id
+
Die diagonal liegenden Schalter 1 und 2 werden
gleichzeitig eingeschaltet. Nach einer halben
Periode werden sie ausgeschaltet und die Schal1
3
uL
ter 3 und 4 eingeschaltet. Am Brückenausgang
entsteht eine rechteckförmige Wechselspannung.
iL
L
R
Zwischen den Steuerimpulsen für die Schalter 1
Ud
und 4 (bzw. 2 und 3) ist eine Totzeit to notwendig, damit kein Kurzschluß bei ungleich schnell
schaltenden Bauelementen entstehen kann. Da4
2
mit ist die Betriebsfrequenz eingeschränkt. Allerdings erzeugen hohe Betriebsfrequenzen hohe
Schaltverluste.
In der Praxis bestimmen die thermischen Verluste die maximale Betriebsfrequenz!
Bei induktiver Last (meist der Fall) hat der Strom nach dem Umschalten der Spannung einen exponentiell ansteigenden
(abfallenden) Verlauf. Daher sind für die Zeit nach der Spannungsumkehr Dioden notwendig, die den Strom solange
führen, bis auch dieser seine Richtung umgekehrt hat. In dieser Phase wird Energie in den Gleichstromkreis zurückgespeist (daher auch Rückspeisedioden!).
Ohm’sche Last
Induktive Last
uL
uL
Ud
Ud
t
- Ud
t
- Ud
T
iL
T
iL
t
t
id
id
t
Id
t
Ausgangsgrößen des Wechselrichters (Wechselstromseite)
Spannungen:
ohmsche Last
u$ L = U d
4
u$1L = U d
π
induktive Last dominiert
u$ L = U d
4
u$1L = U d
π
Scheitelwert
i$L = U d / R
Effektivwert
I L = Ud / R
4 Ud
i$1L =
π R
1 4 Ud
I1L =
2π R
T Ud
i$L =
4 L
I L = i$L / 3
2T U
i$1L = 2 d
π L
2 U
I1L = 2 T d
L
π
Scheinleistung gesamt
S = U d2 / R
S = I LU d =
Grundschw. scheinleistung
S1 =
Wirkleistung gesamt
P = U d2 / R
P≈
Grundschwingungsfaktor
g = S1 / S = 0,81
g = 0, 89
Scheitelwert
Scheitelwert d. Grundschw.
Strom:
Scheitelwert d. Grundschw.
Effektivwert d. Grundschw.
Leistung:
8 U d2
π2 R
S1 =
T
U d2
4 3L
4T U d2
π3 L
U d2
48τ 2 f 2 R
mit τ = L / R
Eingangsgrößen des Wechselrichters (Gleichstromseite):
Ud
Ud
Gleichstrommittelwert
Id = I L = Ud / R
Effektivstrom
I dRMS = I L = U d / R
Ud
Id ≈
48τ 2 f 2 R
T Ud
I dRMS =
4 3 L
ges. Scheinleistung
S = P = U d2 / R
Spannung:
Strom:
Leistung:
S ≈U d I dRMS =
T U d2
4 3 L
aufgenommene Wirkleistung =abgegebene Wirkleistung!
Steuern der Ausgangsleistung:Über die Gleichspannung Ud, die Frequenz f=1/T oder die Pulsbreite T1:
Für ohm'sche Last gilt:
U L = Ud
2T1
T
IL =
Steuersignal
Ud
R
2T1
T
P=
U d2 2T1
R T
Wird das Tastverhältnis T1/T = 1/3 gewählt, werden die Oberschwingungen zugunsten der Grundschwingung reduziert! (Die dritte Oberschwingung verschwindet)
t
T1
T
Ausgangsleistung eines einphasigen Wechselrichters
1
0,01
0,02
0,03
0,04
0,06
0,10
0,16
0,25
0,40
0,63
1,00
1,58
2,51
3,98
6,31
10,00
Leistungsfaktor
0,1
Wirkleistung
normiert
0,01
Wirkleistung
0,001
0,0001
Frequenz * Lastzeitkonstante f* τ
Oberschwingungen beim einphasigen Wechselrichter
1,2
1
G rundschwingung
0,8
2*PHI
0,6
Oberschwingung mit der Ordnungszahl v
0,4
v = 3
0,2
v = 5
v = 11
v = 7
v = 9
0
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
-0,2
-0,4
Ausschaltphase
PHI
Grund- und Oberschwingungsfaktor des einphasigen Wechselrichters
1,200
1,000
0,800
0,600
0,400
g=
k=
0,200
0,000
0
5
10
15
20
25
30
35
40
45
50
Ausschaltphase PHI
55
60
65
70
75
80
85
90
Spannungsdimensionierung der Schalter
Durch das Abschalten des Transistors T1 kommutiert der Laststromes, der zu
diesem Zeitpunkt gerade seinen Scheitelwert erreicht hat, von T1 nach D4.
Dadurch entsteht an der Induktivität der Zuleitungen Ls eine Spannungsspitze.
Diese muß u. U. durch Beschaltungskondensatoren in der Höhe begrenzt werden.
Kurz vor der Kommutierung ist infolge des Laststromes in der Induktivität Ls
Energie gespeichert:
i Ls = i$L WLs = Ls * i$L2 / 2
U CE 1 = 0
T1
R
D1
C
Ls
T4
R
IL
Last
C
D4
Nach der Kommutierung:
Die Energie der Streuinduktivität schwingt in den Kondensator über und erzeugt an diesem die Überspannung ∆U.
Die zulässige Transistorsperrspannung UCE max muß größer als die Summe von Batteriespannung und Überspannung sein!
i Ls = 0 WLs = C∗ ∆U 2 / 2
U CE = U d + ∆U < U CE max
Durch Vergrößern des Beschaltungskondensators C wird die Überspannung geringer. Die Überspannung klingt in
einer gedämpften Schwingung ab. Der Kondensator hat beim Wiedereinschalten des Transistors die Spannung Ud
und wird über den Transistor entladen. Der Widerstand R begrenzt diesen Entladestrom.
Dreiphasenwechselrichter:
Zweistufenwechselrichter (Blockwechselrichter):
Werden drei Ventilzweige zur Erzeugung einer dreiphasigen Ausgangsspannung verwendet, so müssen diese um
T/3 zeitlich versetzt getaktet werden. In jedem Ventilzweig werden das obere und das untere Ventil wie beim einphasigen Wechselrichter jeweils im Gegentakt geschaltet. Als Außenleiterspannung entstehen Spannungsblöcke
mit dem Scheitelwert Ud und einer Dauer von T/3. Aufgrund dieser Spannungsform wird diese Schaltung mit
diesem Betrieb als Blockwechselrichter bezeichnet.
+
UV
Ud
=
2
Ud
=
2
3
1
5
Ud
M
4
6
V
U
i
U
i
W
i
N
U
0
120
240
360
480
0
120
240
360
480
W
i
U
ωt
2
U
V
UN
D1
UV
T1
D4 T4
ωt
D1
Zweistufen WR
2 / 3 = 0,817
2 3 / π = 1103
,
2 / 3 = 0,471
2 / π = 0,637
Ud
3/π
Effektive verkett.Spg. UUV/Ud
Grundschwingungsampl. d. verk. Spg. Û1UV/Ud
Effektive Phasenspg. UUN/Ud
Grundschwingungsampl. d. Phasenspg.Û1UN/Ud
Ventilspannung (ohne Überspannungsspitzen)
Grundschwingungsfaktor g = U1 UV/UUV
Pulswechselrichter:
In der oben gezeichneten Schaltung werden die Ventile eines Zweiges mit einer hohen Taktfrequenz (einige kHz)
so geschaltet, daß die Spannung an einer Phase aus Pulsen mit sinusförmig variierender Breite besteht. Wird diese
Ausgangsspannung über ein Tiefpaßfilter geführt, so wird die Ausgangsspannung sinusförmig. Voraussetzung
sind schnell schaltende Ventile mit niedrigen Schaltverlusten (meist IGBT’s, oder auch MOSFET’s oder Bipolare
Transistoren). Damit können Asynchronmotoren nahezu ideal in einem sehr weiten Drehzahlbereich verlustarm
angetrieben werden.
Blockschaltbild eines kompletten Pulswechselrichters:
Netz
1~, 3~
Gleichrichter
Zwischenkreis
Id
Wechselrichter Motorfilter
Ud
Motor (ASM)
U
V
W
U N , cos ϕ N
U M I M cos ϕ Μ
Das Netzfilter dient zur Reduzierung der Netzstromoberschwingungen. Der Gleichrichter erzeugt die Zwischenkreis-Gleichspannung. Soll diese verändert werden, wird ein gesteuerter Gelichrichter verwendet. Der Zwischenkreiskondensator glättet die Zwischenkreisspannung. Die Glättungsdrossel im Zwischenkreis dient insbesondere
bei höheren Leistungen zur Verbesserung des Leistungsfaktors des Netzstromes. Der Wechselrichter dient zur
Erzeugung der dreiphasigen Wechselspannung. Das Motorfilter glättet die Ausgangsspannung und verhindert
einen ausgangsseitigen Totalkurzschluß des Wechselrichters.
Das nachstehende Bild zeigt, wie groß die Einschaltdauern von Transistor und Diode während einer Pulsperiode
sind, wie die Spannung einer Phase zwischen +Ud/2 und - Ud/2 geschaltet wird und wann die Transistoren bzw.
die Rückspeisedioden den Laststrom führen. Je größer die Phasenverschiebung zwischen Motorspannung und –
strom ist, desto größer wird der Diodenstrom, entsprechend kleiner der Transistorstrom und bei ϕ > 90 0 speist
der Motor Energie in den Gleichstromzwischenkreis zurück. In diesem Fall muß entweder der
Zwischenkreiskondensator die Energie aufnehmen (geht nur sehr kurze Zeit) oder ein zugeschalteter
Bremswiderstand vernichtet diese Energie. Bei längerer Rückspeisung (Bahnen) speist eine antiparallele
Gleichrichterschaltung diese Energie ins Netz zurück.
E inschaltdauer
100 %
Transistor T1
Transistor T4
D io d e D 1
50 %
D iode D 1
D iode D 4
0 %
Spannung
Strom
Transistor T1
D io d e D 4
Größen des PWR:
Motor:
P = 3 * U M * I M * cosϕ
Wechselrichter:
U UV = U M =
Zwischenkreis:
Id = P / Ud
Id =
i$M = 2 I M
3 Ud
= 0,612 * U d
2 2
(Sinusbewertete Modulation)
(Gleichstrommittelwert)
3P
3
= IM
cosϕ = 1,06 * I M * cosϕ (Sinusbewertete Modulation)
2 2U M
2 2