Blatt 3 - Uni Regensburg/Physik

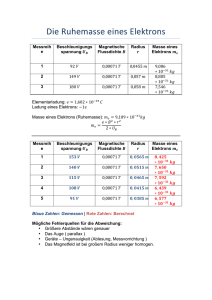
Übungen zur Vorlesung Aufbau der Materie 2b
SoSe 16
C. Uebler, P. Plössl, N. Offen
Blatt 3
—
Ausgabe: 26.4.2016
—
Abgabe: 3./4.5.2016
Aufgabe 8: ”Photon-Zerfall” und Elektron-Positron-Vernichtung
In der Vorlesung wurde der Prozess der Paarvernichtung angesprochen, wobei ein Elektron e− und ein Positron e+ übergehen in ein Photon γ,
e− + e+ → γ.
(1)
a) Wie groß ist die Ruhemasse und Ladung des Elektrons bzw. Positrons?
b) Wir wissen bereits, daß Photonen keine Ruhemasse besitzen, weswegen das Quadrat des Vierer-Impuls pγ des Photons verschwindet, p2γ = 0. Ist obiger Prozess
überhaupt kinematisch möglich für p2γ = 0? Begründen Sie Ihre Antwort.
Betrachten wir nun den umgekehrten Prozess γ → e− + e+ .
c) Ist obiger Prozess möglich für p2γ = 0?
d) Ist es möglich in ein Bezugssystem zu wechseln, in dem das Photon in Ruhe ist?
Aufgabe 9: Compton-Streuung
Ein Photon γ mit Vierer-Impuls (kµ ) = (E/c, ~k) wird an einem ruhenden Elektron e−
mit Vierer-Impuls pµ und Ruhemasse me gestreut. Nach der Streuung hat das Photon
den Vierer-Impuls k′µ und das Elektron den Vierer-Impuls p′µ .
a) Skizzieren Sie den Prozeß. Welche Beziehung zwischen den Vierer-Impulsen kµ , pµ ,
k′µ , p′µ folgt aus der Erhaltung des Vierer-Impulses?
b) Wie groß ist die Ruhemasse des Photons? Wie groß ist k2 ? Welche Beziehung
zwischen E und |~k| folgt daraus?
c) Wie groß ist k′2 ? Welche Beziehung zwischen E ′ und |~k′ | folgt daraus?
d) Welche nicht-verschwindenden Komponenten hat pµ . Wie groß ist p2 ? Was folgt
daraus für die nicht-verschwindenden Komponenten von pµ ? Wie groß ist p′2 ?
e) Welche Beziehung besteht zwischen dem Skalarprodukt ~k · ~k′ der beiden (Dreier)Impulse ~k, ~k′ und ihrer Beträge |~k|,|~k′ | und dem Zwischen- bzw. Streuwinkel θ.
f ) Zeigen Sie, daß die Energie des gestreuten Photons E ′ = k′0 durch
E′ =
E
1+
E
(1
me c2
− cos θ)
(2)
gegeben ist.
g) Fassen wir nun das Photon als Lichtwelle auf. Welche Beziehung besteht zwischen
Energie und Wellenlängen einer Lichtwelle? Ist die Wellenlänge der gestreuten
Lichtwelle größer oder kleiner als die der einfallenden Lichtwelle?
Hinweise:
ˆ Vierer-Impulserhaltung besagt k+p = k ′ +p′ und ist eine Möglichkeit, die klassische
Energie- und Impulserhaltung in eine Gleichung zu schreiben.
ˆ Berechnen Sie in Teilaufgabe f) (p − p′ )2 und (k ′ − k)2 und setzen Sie beide Ausdrücke in Beziehung mittels der Vierer-Impulserhaltung. Ersetzen Sie dann die
Energie Ee′ = p′0 des gestreuten Elektrons mittels Energieerhaltung durch E, E ′
und me und lösen nach E ′ auf.
Aufgabe 10: Schwerpunkts-Energie bei einer Zwei-Teilchen-Streuung
Die Schwerpunktsenergie ECM wird für eine elastische Zwei-Teilchen-Streuung über
p
ECM = c2 (p1 + p2 )2
definiert, wobei p1 und p2 die Vierer-Impulse der beiden beteiligten Teilchen sind. Nehmen Sie nun an, es werden identische Teilchen gestreut.
a) Drücken Sie die Schwerpunktsenergie durch die Energien der beiden beteiligten
Teilchen im Schwerpunktssystem aus.
b) Drücken Sie die Schwerpunktsenergie durch die Energien der beiden beteiligten
Teilchen im Ruhesystem eines der beiden Teilchen aus.
c) Was bedeutet dies für die Schwerpunktsenergie von Collider- und Fixed-TargetExperimenten? In welchem Experimenttyp lassen sich höhere Schwerpunktsenergien erreichen?
Aufgabe 11: Neutron-Zerfall (Staats-Examen Herbst 2013)
Original-Text: In einer Nebelkammer werden beim Betazerfall eines freien ruhenden
Neutron, das sich in einem homogenen Magnetfeld mit der magnetischen Flussdichte
B=0.050T befindet, die Kreisbahnen des enstehenden Protons und Elektrons beobachtet. Die Kreisbahnen liegen senkrecht zu den Magnetfeldlinien. Für den Bahnradius des
Protons misst man rp = 65mm und für den Bahnradius des Elektrons re = 33mm.
Nehmen Sie für die folgenden Rechnungen vereinfachend an, daß die Ruhemasse des
Antineutrinos vernachlässigt werden kann.
Hinweis: Ein freies Neutron n zerfällt in ein Proton p, ein Elektron e− und ein Antineutrino ν̄e : n → p + e− + ν̄e .
a) Berechnen Sie den Impuls und die kinetische Energie (in eV) des Protons und
des Elektrons! Rechnen Sie dabei für das Proton klassisch und für das Elektron
relativistisch!
Hinweis: Die Lorentzkraft liefert für den Impuls eines Teilchens mit der Elementarladung e und einem Bahnradius r in einem Magnetfeld der magnetischen Flussdichte B die klassisch und relativistisch gültige Beziehung: p = eBr.
(Ersatzlösung für kinetische Energie des Protons = 400 eV und für kinetische
Energie des Elektrons = 180 keV).
b) Berechnen Sie aus dem Massendefekt der Reaktion die gesamte kinetische Energie
(in eV), die Proton, Elektron und Antineutrino zusammen besitzen.
(Ersatzlösung: 700keV)
c) Berechnen Sie die Gesamtenergie des Antineutrinos in der Einheit Elektronenvolt!
d) Berechnen Sie den Impuls des Antineutrinos!
e) Begründen Sie, warum ein freies Proton NICHT in ein Neutron n, Positron e+ und
Neutrino νe zerfallen kann: p 6→ n + e+ + νe .