AB B2 B1 - an der ZHAW

1
Rekursion in Relationalen Datenbanken
April 2010
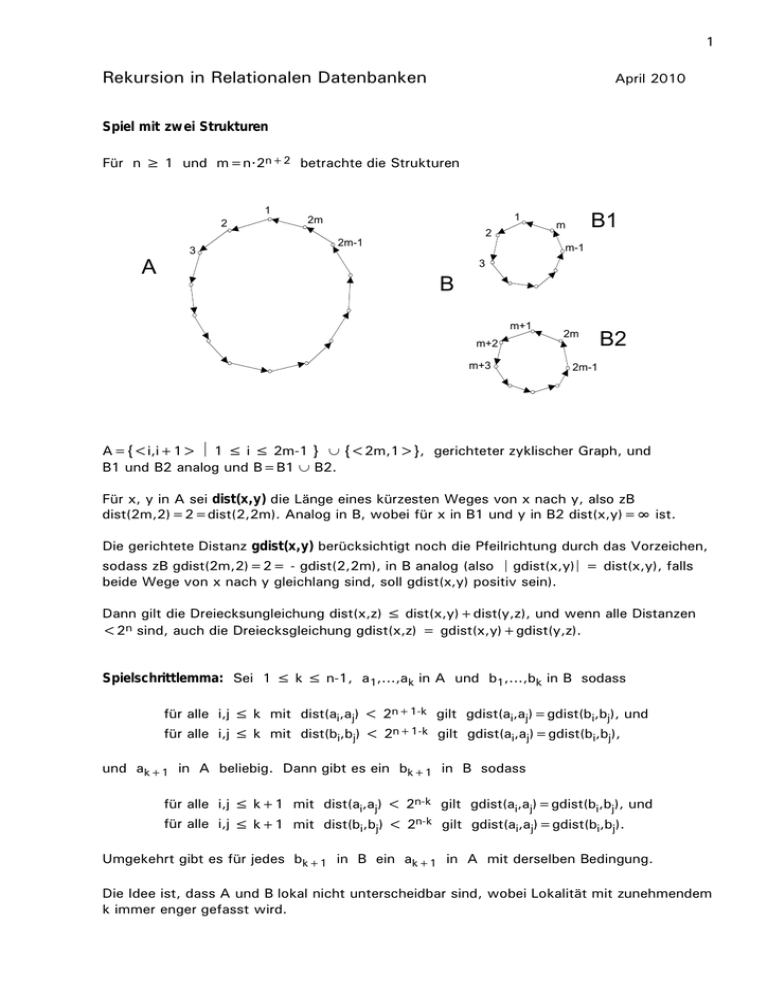
Spiel mit zwei Strukturen
Für n ≥ 1 und m=n.2n+2 betrachte die Strukturen
1
2
1
2m
2
3
A
2m-1
B1
m
m-1
3
B
m+1
m+2
m+3
2m
B2
2m-1
A={<i,i+1>  1 ≤ i ≤ 2m-1 }  {<2m,1>}, gerichteter zyklischer Graph, und
B1 und B2 analog und B=B1  B2.
Für x, y in A sei dist(x,y) die Länge eines kürzesten Weges von x nach y, also zB
dist(2m,2)=2=dist(2,2m). Analog in B, wobei für x in B1 und y in B2 dist(x,y)=∞ ist.
Die gerichtete Distanz gdist(x,y) berücksichtigt noch die Pfeilrichtung durch das Vorzeichen,
sodass zB gdist(2m,2)=2= - gdist(2,2m), in B analog (also ∣ gdist(x,y)∣ = dist(x,y), falls
beide Wege von x nach y gleichlang sind, soll gdist(x,y) positiv sein).
Dann gilt die Dreiecksungleichung dist(x,z) ≤ dist(x,y)+dist(y,z), und wenn alle Distanzen
<2n sind, auch die Dreiecksgleichung gdist(x,z) = gdist(x,y)+gdist(y,z).
Spielschrittlemma: Sei 1 ≤ k ≤ n-1, a1,...,ak in A und b1,...,bk in B sodass
für alle i,j ≤ k mit dist(ai,aj) < 2n+1-k gilt gdist(ai,aj)=gdist(bi,bj), und
für alle i,j ≤ k mit dist(bi,bj) < 2n+1-k gilt gdist(ai,aj)=gdist(bi,bj),
und ak+1 in A beliebig. Dann gibt es ein bk+1 in B sodass
für alle i,j ≤ k+1 mit dist(ai,aj) < 2n-k gilt gdist(ai,aj)=gdist(bi,bj), und
für alle i,j ≤ k+1 mit dist(bi,bj) < 2n-k gilt gdist(ai,aj)=gdist(bi,bj).
Umgekehrt gibt es für jedes bk+1 in B ein ak+1 in A mit derselben Bedingung.
Die Idee ist, dass A und B lokal nicht unterscheidbar sind, wobei Lokalität mit zunehmendem
k immer enger gefasst wird.
2
Beweis des Spielschrittlemma:
Fall: für alle i ≤ k ist dist(ai,ak+1) ≥ 2n-k. Dann wähle bk+1 in B sodass für
alle i ≤ k gilt dist(bi,bk+1) ≥ 2n-k. Beachte dass dies in jedem Falle möglich ist weil
es für jedes k Lücken ohne bereits gewählte Elemente gibt von mindestens der Länge
m/k, also > m/n = 2n+2.
Fall: es gibt ein i ≤ k mit dist(ai,ak+1) < 2n-k. Dann wähle bk+1 in B sodass
gdist(ai,ak+1)=gdist(bi,bk+1).
Wir zeigen: für j ≤ k und dist(aj,ak+1) < 2n-k gilt gdist(aj,ak+1)=gdist(bj,bk+1).
Gemäss Konstruktion gibt es ein i ≤ k mit dist(ai,ak+1) < 2n-k und
gdist(ai,ak+1)=gdist(bi,bk+1). Damit ist wegen der Dreiecksungleichung dist(ai,aj) ≤
dist(ai,ak+1)+dist(aj,ak+1) < 2n-k +2n-k =2n+1-k und deshalb nach (Induktions-)
Voraussetzung gdist(ai,aj)=gdist(bi,bj). Da alle beteiligten Distanzen < 2n sind, gilt mit
gdist(ai,ak+1)=gdist(bi,bk+1) und gdist(ai,aj)=gdist(bi,bj) wegen der Dreiecksgleichung
aber auch gdist(aj,ak+1)=gdist(bj,bk+1).
Der Beweis dass für j ≤ k und dist(bj,bk+1) < 2n-k gilt gdist(aj,ak+1)=gdist(bj,bk+1)
verläuft völlig symmetrisch.
Beachte dass der Beweis nur Eigenschaften der Strukturen A und B benutzt hat, welche
beiden gemeinsam sind. Deshalb gilt auch die Richtung von bk+1 in B nach ak+1 in A.
Spielt man also n Schritte dieses Spieles, mit beliebigem a1 in A und b1 in B beginnend,
und in jedem nächsten Schritt ein beliebiges ak+1 in A oder bk+1 in B wählend und ein
jeweiliges gemäss Spielschrittlemma korrespondierendes bk+1 in B oder ak+1 in A
dazunehmend, so hat man nach n Schritten einander korrespondierende Elemente a1,...,an
in A und b1,...,bn in B sodass
für alle i,j ≤ n mit dist(ai,aj) < 2 gilt gdist(ai,aj)=gdist(bi,bj).
A und B als Modelle binärer Relationen
Betrachten wir eine Sprache L die als einziges nichtlogisches Symbol, also nebst der
Gleichheit, ein binäres Relationssymbol R(.,.) hat. Dann werden A und B durch die
Interpretationen
A ⊨ R(a,a’) iff gdist(a,a’)=1 in A, und
B ⊨ R(b,b’) iff gdist(b,b’)=1 in B
zu Modellen der Sprache L. Nun betrachten wir einen beliebigen Satz von L in pränexer
Form mit n Quantoren
 ≡ Q1x1Q2x2....Qnxn (x1,x2,...,xn), mit Qk{,} und  quantorenfrei
3
Behauptung: Dann ist A ⊨  iff B ⊨  , das heisst der Satz ist gültig in A genau dann
wenn er gültig ist in B.
Beweis: Wir nehmen oBdA an dass A ⊨  und B ⊨  . Die Negation  ist dann
äquivalent zu Q1’x1Q2’x2....Qn’xn (x1,x2,...,xn), wobei für jedes k Qk’= ist falls Qk=
ist und umgekehrt. Wiederum oBdA nehmen wir noch an dass Q1= ist. Wegen
A ⊨ x1Q2x2....Qnxn (x1,x2,...,xn) gibt es dann ein a1 in A mit
A ⊨ Q2x2....Qnxn (a1,x2,...,xn). Wähle b1 in B beliebig. Wegen
B ⊨ x1Q2’x2....Qn’xn (x1,x2,...,xn) gilt dann
B ⊨ Q2’x2....Qn’xn (b1,x2,...,xn).
Ist im nächsten Schritt Q2 der  Quantor, dann nehmen wir ein a2 in A mit
A ⊨ Q3x3....Qnxn (a1,a2,x3,...,xn) und ein korrespondierendes b2 in B gemäss
Spielschrittlemma, für das dann
B ⊨ Q3’x3....Qn’xn (b1,b2,x3,...,xn) gilt weil ja in diesem Fall Q2’= ist. Ist aber Q2’ der
 Quantor, dann nehmen wir zuerst ein b2 in B sodass
B ⊨ Q3’x3....Qn’xn (b1,b2,x3,...,xn), und dann ein korrespondierendes a2 in A gemäss
Spielschrittlemma, für das dann
A ⊨ Q3x3....Qnxn (a1,a2,x3,...,xn) gilt (wegen Q2= in diesem Fall).
Auf diese Art fahren wir weiter, von ak+1 zu bk+1 falls Qk+1 der Existenzquantor ist, und
umgekehrt, sodass wir nach n Schritten einander gemäss Spielschrittlemma
korrespondierende Elemente a1,...,an in A und b1,...,bn in B haben mit
A ⊨ (a1,a2,a3,...,an) und B ⊨ (b1,b2,b3,...,bn).
Wegen dem Spielschrittlemma und der Interpretation von R(.,.) in A und B ist dann
A ⊨ R(ai,aj) iff B ⊨ R(bi, bj), und weil  quantorenfrei ist deshalb
für alle i,j ≤ n
auch A ⊨ (a1,a2,a3,...,an) iff B ⊨ (b1,b2,b3,...,bn), was einen Widerspruch darstellt.
Das bedeutet, dass connectivity nicht ausdrückbar ist in der Logik (erster Stufe), das heisst
es gibt keinen Satz  der Sprache L welcher in einem Modell A zur Sprache L (={R(.,.)})
genau dann gültig ist, wenn der durch A definierte Graph zusammenhängend ist.
Damit ist auch transitive closure nicht ausdrückbar, denn gäbe es eine Formel (x1,x2) die
in allen Modellen A mit Elementen a1,a2 in A genau dann gültig wäre, A ⊨ (a1,a2) , wenn
<a1,a2> oder <a2,a1> zur transitiven Hülle des durch A definierten Graphen gehören, so
wäre
x1x2(x1=x2 ∨ (x1,x2)) ein Satz der connectivity ausdrückt.
(die transitive Hülle von A, transitive closure, ist
A* = {<x,y>  x0,x1,...,xn  i<n <xi,xi+1>  A})
4
Zusammenhang mit der Relationalen Algebra
Relationen werden üblicherweise als Teilmengen von Produkten von Wertebereichen
genommen, r  D1  D2  D3 und die Operationen via Begriffswelt von Mengen definiert,
zum Beispiel die Projektion von r auf D1 und D2 als
1,2(r) = {<t(1),t(2)>  t  r}  D1  D2
Neben der Projektion werden traditionell noch Selektion, Vereinigung, Differenz sowie ein
Kreuzprodukt als Basisoperationen zur relationalen Algebra gezählt, und je nach Behandlung
der Attribute auch noch ein Renaming, auf das wir uns hier nicht einlassen (mehr dazu
mündlich bei Bedarf).
Statt dieses Tupelkalkül kann man ein gleichmächtiges Domänenkalkül betrachten, welches
formal noch etwas näher an der Logik erster Stufe steht,
1,2(r) = {<x1,x2>  x3 <x1,x2,x3>  r},
oder, mit Relationen als Sprachelementen, R(.,.,.) in unserem Fall,
1,2(r) = {<x1,x2>  x3 R(x1,x2,x3)}.
x3 R(x1,x2,x3) ist eine Formel mit den freien Variablen x1 und x2 , und so definiert jede
Formel (x1,x2,...,xn) einer Sprache die nur Relationszeichen enthält, eine Abfrage, eine
Query respektive eine Sicht auf die Basisdaten R(a1,a2,a3), S(b4,b5,b6,b7,b8), usw, die in
Form von Tabellen gespeichert gedacht sind.
Eine langweilige formale Analyse, durch so schöne Gleichungen wie
{<x1,x2> (x1,x2)}  {<x1,x2>(x1,x2)} = {<x1,x2> (x1,x2)  (x1,x2)}
getragen, zeigt, dass das Kalkül der relationalen Algebra, das Tupelkalkül und das
Domänenkalkül logisch sozusagen gleichmächtig sind, woraus man mit dem oben
Dargestellten dann schliessen kann, dass in der relationalen Algebra die transitive Hülle nicht
darstellbar ist.
Deshalb haben die Hersteller von relationalen Datenbank Systemen und 1999 auch der ANSI
Standard die Abfragesprache SQL erweitert um eine rekursive Komponente.
Die transitive Hülle als Rekursion
Für binäre Relationen R(.,.) und S(.,.) bezeichne R∘S die Zusammensetzung
R∘S = {<a,b>  z(R(a,z) ∧ S(z,b))}
Damit lässt sich für eine binäre Relation E(.,.) die transitive Hülle
E* = {<x,y>  x0,x1,...,xn  i<n <xi,xi+1>  E}
rekursiv beschreiben als E*=E  (E*∘E) ( Fixpunkt von f(X)=E  (X∘E) ).
5
E* ist die kleinste Menge die E enthält mit
<x,y>  E* ∧ <y,z>  E* → <x,z>  E*.
Die Gleichung E*=E  (E*∘E) ist direkt in SQL übersetzt worden, mit E(Links,Rechts) als
WITH ESTAR (Links,Rechts) AS
(SELECT Links, Rechts FROM E
UNION ALL
SELECT x.Links, y.Rechts FROM ESTAR x, E y WHERE x.Rechts=y.Links)
SELECT Links, Rechts
FROM ESTAR
Was aber, wenn das Datenbanksystem keine Rekursion kennt?
Weil Rekursion in SQL erst spät erschienen ist und noch nicht alle Datenbanksysteme
Rekursion implementiert haben, sind Strukturen untersucht worden, die wenigstens gewisse
typische praktische Fragestellungen von transitiven Hüllen ohne Rekursion beantworten
können, wie zum Beispiel das “Parts Explosion Problem“, dh finde in einer hierarchischen
Struktur zu einem Node alle darunterliegenden.
Eine bekanntere unter diesen Strukturen ist das “Nested Set Model“:
a
1
14
aa
2
ab
3
4
ac
9
aba
5
10
13
abb
6
7
aca
8
11
12
Die Numerierung erfolgt top-down, left-right (“preorder traversal“).
Hier wird in einer Relation zum Beispiel E(Node, Down, Up) festgehalten, also
<a,1,14> in E, <aa,2,3> in E, usw. Es ist klar, dass Insert und Delete von Nodes extrem
mühsam sind, hingegen gewisse Abfragen einfach respektive erst möglich ohne Rekursion.
Vor ein paar Jahren habe ich firmenintern die Frage gestellt bekommen, ob es etwas
Aehnliches auch gäbe für nichthierarchische (aber gerichtete azyklische) Graphen, von einem
Problem der firmeninternen “Business Data Language“ stammend, und einem Benutzer der
ein kleines Datenbanksystem verwenden wollte welches Rekursion nicht kennt.
6
Die Antwort war ein mathematisches Paper “A valuation function for finite directed acyclic
graphs“, und ein Strukturvorschlag, nämlich dass man zum gegebenen Graphen (in Form
einer Relation E(Links,Rechts)) eine zweite Relation unterhält,
Wege(Anfang, Ende, Anzahl),
welche zu je zwei Knoten des Graphen, Anfang und Ende, festhalten soll, wieviele
verschiedene Wege vom einen zum anderen führen.
Aenderungen des Graphen führen zwar ebenfalls zu Aenderungen ganzer Mengen von
Tupeln in “Wege“, aber sie sind einfacher zu verstehen. Soll zum Beispiel die Kante <a,b>
neu in E eingefügt werden,
y
b
x
a
so erhöht sich die Anzahl Wege von x nach y um die Anzahl Wege von x nach a,
multipliziert mit der Anzahl Wege von b nach y,
Anzahlneu(x,y):=Anzahlalt(x,y) + Anzahlalt(x,a).Anzahlalt(b,y), für x,y ∉ {a,b}, usw.
Allerdings darf man froh sein, dass anständige Systeme mittlerweile die Rekursion in SQL
kennen:
Andere Beispiele aus der Praxis:
In einem ETL-tool (Extract-Transform-Load) sollen Abhängigkeiten definiert werden zwischen
Tabellen, weil wenn eine Tabelle eine referentielle Abhängigkeit zu einer anderen hat, muss
diese andere zuerst geladen werden.
Weil der Abhängigkeitsgraph E(Nachher,Vorher) hunderte von Einträgen hat, möchte man
ihn möglichst redundanzfrei haben, das heisst, bei jedem vorhandenen Pfad
x0,x1,...,xn mit n>1 und  i<n <xi,xi+1>  E
7
im Sinne der Nachher-Vorher Abhängigkeit muss <x0,xn> nicht auch noch festgehalten
werden, weil es sich von selbst ergibt.
Diese Aufgabenstellung ist die gegenteilige des Suchens der transitiven Hülle,
mit E>1 =(E∘E )  (E>1∘E) ist E \ E>1 gesucht, sehr direkt in SQL übersetzt:
WITH Egroessereins(Nachher,Vorher) AS
(SELECT x.Nachher, y.Vorher FROM E x, E y
WHERE x.Vorher=y.Nachher
UNION ALL
SELECT x.Nachher, y.Vorher FROM Egroessereins x, E y
WHERE x.Vorher=y.Nachher)
SELECT Nachher, Vorher FROM E
EXCEPT ALL
SELECT Nachher, Vorher FROM Egroessereins
Natürlich wurde in diesem Praxisbeispiel ein strenger mathematischer Beweis dafür gemacht
bzw vorgelegt, dass die Lösung nicht zuviel eliminiert aus dem ursprünglich gegebenen
Graphen, da natürlich alle Abhängigkeiten eingehalten werden müssen (sonst stürzen die
Jobs im ETL tool ab...).
Etwas präziser, zwei Nodes die durch einen Pfad verbunden sind, müssen auch nach der
Redundanz Elimination noch durch (mindestens) einen Pfad verbunden sein.
Ein anderes Praxisbeispiel ist die Beantwortung von Fragen zu Abhängigkeiten von Firmen im
Konzern, beispielsweise mit
Particip(FinYear,Version,Simtyp,Parent,Child,Share_Perc,Share_Nom)
die Frage nach dem maximalen Abhängigkeitslevel, nach indirekten Abhängigkeiten, nach
Zyklen, usw. (Version ist zB ’factual’, ’plan’, projections ’P1’, ’P2’, usw).