Mathematische Formel für Vielfalt des Denkens
Werbung

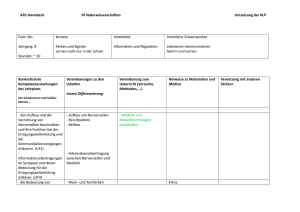
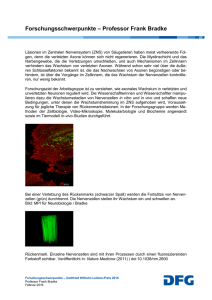
22 WISSENSCHAFT & WETTER Mittwoch, 4. Januar 2006 Mathematische Formel für Vielfalt des Denkens Kurz notiert Göttinger Max-Planck-Forscher entwickelt neues Modell für Entwicklung des Gehirns Pflanzenbau: „Pflanzenbauliche Versuche zur integrierten Kontrolle von Rhizoctonia solani an Zuckerrübe und Mais: Einfluss von Sortenwahl und Fruchtfolge“: Dr. Stephanie Kluth, Institut für Zuckerrübenforschung, Göttingen. Institut für Pflanzenbau und Pflanzenzüchtung, Von-Siebold-Straße 8, Kurssaal L02, um 16.15 Uhr. Pflanzenpathologie: „Einfluss einer mehrjährig differenzierten Bodenbearbeitung auf die Befallsdichte und Populationsentwicklung von Schadinsekten in Winterrapskulturen“: Claudia Schierbaum-Schickler. Institut für Pflanzenpathologie und Pflanzenschutz, Grisebachstraße 6, Seminarraum L07 (Erdgeschoss)um 16.15 Uhr. Geowissenschaften: Isotope in den Geowissenschaften“: Prof. Bent T. Hansen. Geowissenschaftliches Zentrum, Goldschmidtstraße, MN 14, um 17.15 Uhr. Ringvorlesung Selbstbestimmung am Lebensende: „Recht auf Euthanasie? Die Patientenverfügung zwischen Lebensschutz und Selbstbestimmung“: Prof. Volker Lipp, Juristische Fakultät. Paulinerkirche, Papendiek 14, um 18.15 Uhr. Neurologie: „Patientenautonomie bei Wachkoma und fortgeschrittener Demenz“: Prof. Hilmar Prange. Klinikum, Robert-Koch-Straße 40, Hörsaal 55, um 17 Uhr. Mittwoch, 4. Januar 2006, um 18.15 Uhr Umweltgeschichte: „Die Historisierung der Natur: Zeit und Raum als Kategorien der Umweltgeschichte. Ein Vergleich zwischen deutschen und USamerikanischen Forschungsansätzen“: Prof. Ursula Lehmkuhl, Berlin. Institut für Zoologie, Anthropologie und Entwicklungsbiologie, Bürgerstraße 50, Hörsaal, um 18.15 Uhr. Wirtschafts- und Sozialgeschichte: „Economic History over the Very Long Run. A Brief Economic History of the World“: Prof. Gregory Clark, University of California. Institut für Wirtschafts- und Sozialgeschichte, Mehrzweckgebäude, Platz der Göttinger Sieben 5, MZG 1616, um 18.15 Uhr. Die Entwicklung des Gehirns in den ersten Lebensmonaten ist abhängig von den Reizen, die empfangen werden. Der Göttinger Neurophysiker Dr. Fred Wolf hat eine Gleichung entwickelt, die erklärt, wie die Gehirnentwicklung zwar strengen mathematischen Gesetzen folgt und andererseits vielfältig im Ergebnis ist. as menschliche Gehirn ist D bei der Geburt noch ein sehr unfertiges Gebilde. Es ähnelt einer Baustelle für ein Haus: Die Baustoffe in Form von Nervenzellen sind zwar bereits reichlich vorhanden, ein Grundgerüst steht auch schon, aber der Aufbau ist noch unvollständig, die Statik provisorisch. Innerhalb weniger Monate entwickelt sich aus diesem wackeligen Gebilde ein stabiles System, in dem Dr. Fred Wolf Milliarden von Nervenzellen auf vielfältigste Weise miteinander verknüpft sind. Wie aber entwickelt sich diese erstaunliche Architektur? Bislang gab es für diesen Prozess nur unzureichende Modelle. Neurophysiker Wolf hat jetzt erstmals eine Gleichung dafür entwickelt, die erklärt, wie die Gehirnentwicklung zwar strengen mathematischen Gesetzen folgt, aber trotzdem jedes Hirn anders „gestrickt“ ist. In seiner Arbeit, die jetzt in dem Fachmagazin „Physical Review Letters“ veröffentlicht wurde, untersucht der Leiter der Forschungsgruppe Theoretische Neurophysik vom Max-Planck-Institut für Dynamik und Selbstorganisation in Göttingen die Entwicklung des visuellen Kortex. In dieser Hirnregion werden optische Eindrücke zuerst verarbeitet. Die dort liegenden Nervenzellen (Neurone) reagieren besonders auf visuelle Elemente, die Konturen markieren. Jede Nervenzelle ist dabei auf eine bestimmte Orientierung spezialisiert: Manche Neurone reagieren auf waagerechte Linien, andere beispielsweise auf Konturen im 30-Grad-Winkel. Damit das Gehirn aus diesen einzelnen Eindrücken ein Bild zusammensetzen kann, kommt es darauf an, wie diese spezialisierten Nervenzellen angeordnet und mit anderen Neuronen verschaltet sind. Mit bildgebenden Verfahren lassen sich inzwischen „Landkarten“ des Gehirns er- sen oder chemischen Reaktionen reagieren bei biologischen Prozessen die einzelnen Elemente nicht nur mit ihren direkten Nachbarn. „Nervenzellen treten vielmehr über weite Distanzen miteinander in Kontakt“, erläutert Wolf. Unterschiedliche Reize Landkarte des Gehirns: Kortikale Orientierungskarte im Sehsystem der Katze. S. Löwel, IfN Magdeburg stellen, die zeigen, wie diese Nervenzellen verteilt sind. So sind Neurone, die auf die gleiche Richtung reagieren, zu Gruppen zusammengefügt, und Bereiche mit einer ähnlichen Orientierung liegen meist nebeneinander. Fähigkeit der Nervenzellen Bisherige Modelle der Hirnentwicklung sagten voraus, dass sich die Anordnung der Nervenzellen wie bei einem Kachelmuster periodisch wiederholt. Tatsächlich ist der Aufbau des Hirns jedoch sehr viel chaotischer, und die Anordnung und Verschaltung der Nervenzellen ist von Hirn zu Hirn völlig verschieden – selbst bei eineiigen Zwillingen. Um diesen Entwicklungsprozess realitätsnäher abbilden zu können, hat der Göttinger Neurophysiker in die Modellbildung eine Fähigkeit der Nervenzellen einfließen lassen, die bei den bisherigen Modellen nicht berücksichtigt worden war: Anders als bei physikalischen Prozes- Bei den Aktivitäten des Gehirns gibt es gewissermaßen viele „Ferngespräche“, die über unzählige Stationen laufen. Deshalb ist die Entwicklung des Hirns auch viel komplexer. Der Selbstorganisationsprozess beginnt bereits in den ersten Tagen nach der Geburt. Ständig entstehen neue neuronale Kontakte und werden andere wieder gelöst – eine Baustelle bei laufendem Betrieb. Da jedes Kleinkind völlig unterschiedlichen Reizen ausgesetzt ist, ist auch der Aufbau der Verschaltungen individuell völlig verschieden. Für diesen verwickelten Prozess hat Wolf nun eine Gleichung gefunden, die eine sehr große Zahl von Mustern zulässt, deren Entstehung mit den gleichen mathematischen Gesetzen vereinbar ist. Die von ihm gefundene mathematische Formel ermöglicht damit jene Vielfalt, die auch das menschliche Denken auszeichnet. Heidi Niemann Mittwoch, 4. Januar Die Wissenschaftsredaktion ist per E-Mail erreichbar: [email protected]