Prof. Dr. K. Kassner Kosmologie (WPF Vertiefungsrichtung) Blatt 2

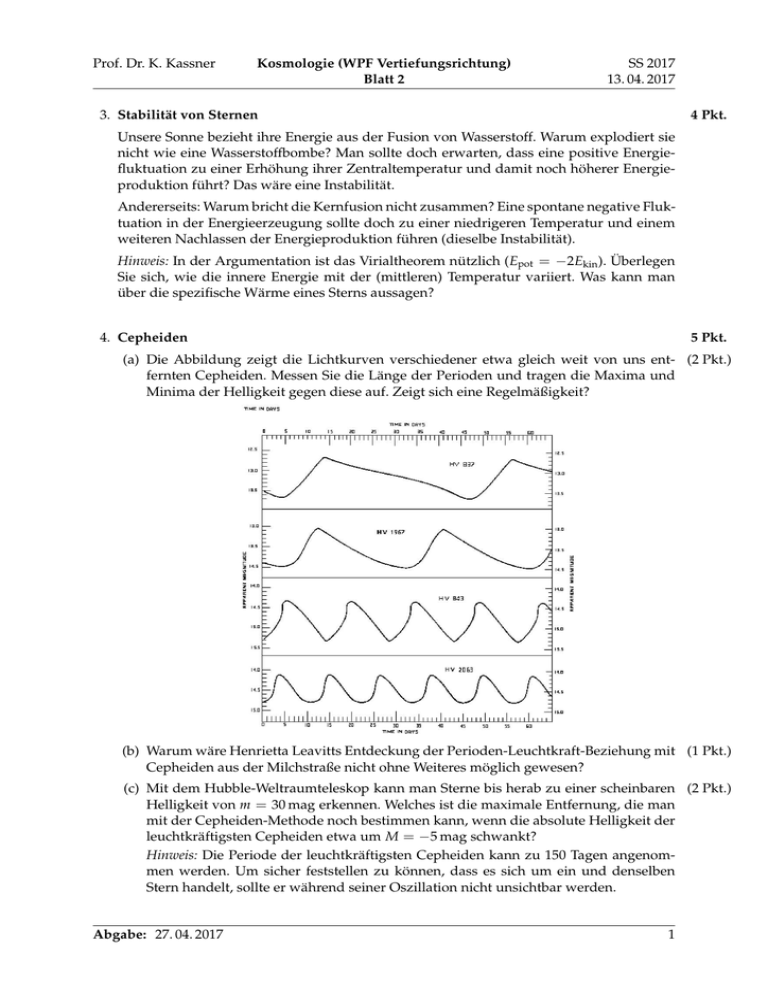
Prof. Dr. K. Kassner
Kosmologie (WPF Vertiefungsrichtung)
Blatt 2
SS 2017
13. 04. 2017
3. Stabilität von Sternen
4 Pkt.
Unsere Sonne bezieht ihre Energie aus der Fusion von Wasserstoff. Warum explodiert sie
nicht wie eine Wasserstoffbombe? Man sollte doch erwarten, dass eine positive Energiefluktuation zu einer Erhöhung ihrer Zentraltemperatur und damit noch höherer Energieproduktion führt? Das wäre eine Instabilität.
Andererseits: Warum bricht die Kernfusion nicht zusammen? Eine spontane negative Fluktuation in der Energieerzeugung sollte doch zu einer niedrigeren Temperatur und einem
weiteren Nachlassen der Energieproduktion führen (dieselbe Instabilität).
Hinweis: In der Argumentation ist das Virialtheorem nützlich (Epot = −2Ekin ). Überlegen
Sie sich, wie die innere Energie mit der (mittleren) Temperatur variiert. Was kann man
über die spezifische Wärme eines Sterns aussagen?
4. Cepheiden
5 Pkt.
(a) Die Abbildung zeigt die Lichtkurven verschiedener etwa gleich weit von uns ent- (2 Pkt.)
fernten Cepheiden. Messen Sie die Länge der Perioden und tragen die Maxima und
Minima der Helligkeit gegen diese auf. Zeigt sich eine Regelmäßigkeit?
(b) Warum wäre Henrietta Leavitts Entdeckung der Perioden-Leuchtkraft-Beziehung mit (1 Pkt.)
Cepheiden aus der Milchstraße nicht ohne Weiteres möglich gewesen?
(c) Mit dem Hubble-Weltraumteleskop kann man Sterne bis herab zu einer scheinbaren (2 Pkt.)
Helligkeit von m = 30 mag erkennen. Welches ist die maximale Entfernung, die man
mit der Cepheiden-Methode noch bestimmen kann, wenn die absolute Helligkeit der
leuchtkräftigsten Cepheiden etwa um M = −5 mag schwankt?
Hinweis: Die Periode der leuchtkräftigsten Cepheiden kann zu 150 Tagen angenommen werden. Um sicher feststellen zu können, dass es sich um ein und denselben
Stern handelt, sollte er während seiner Oszillation nicht unsichtbar werden.
Abgabe: 27. 04. 2017
1
Kosmologie
SS 2017
5. Chandrasekhar-Masse
14 Pkt.
Wenn ein Stern seinen nuklearen Brennstoff erschöpft hat, bleibt ihm als einzige Möglichkeit, den durch die Gravitation erzeugten Druck auszugleichen, der Widerstand, den
ein Fermigas aufgrund des paulischen Ausschließungsprinzips seiner Kompression entgegensetzt. Ein entartetes Fermigas hat selbst bei verschwindender Temperatur noch einen
endlichen Druck.
Wie Chandrasekhar zeigte, reicht dieser Gegendruck nicht aus, den Stern zu stabilisieren,
wenn seine Masse einen gewissen Grenzwert überschreitet. Unterhalb dieser Grenzmasse
ist das Endstadium des Lebens eines Sterns die Existenz als Weißer Zwerg, dessen mechanisches Gleichgewicht durch die Entartung des Elektronengases aufrecht erhalten wird.
Liegt die Masse des Sterns oberhalb der Grenzmasse, so kann durch Rekombination von
Elektronen und Protonen zu Neutronen aus dem Weißen Zwerg ein Neutronenstern mit
mehr als milliardenfach höherer Dichte entstehen, stabilisiert durch den Entartungsdruck
der Neutronen. Ist jedoch die Masse zu hoch, so reicht auch dieser Druck nicht zur Stabilisierung des Sterns und es entsteht ein schwarzes Loch.
Wir wollen in dieser Aufgabe einige der Überlegungen nachvollziehen, die die Existenz
einer Grenzmasse zeigen und diese auch abschätzen.
(a) Begründen Sie, dass für mechanisches Gleichgewicht einer kugelsymmetrischen Mas- (2 Pkt.)
senverteilung unter ihrer Eigengravitation gelten muss
dp
m (r ) ρ (r )
= −G
,
dr
r2
(5.1)
wo p(r ) der Druck im Abstand r vom Zentrum, m(r ) die in der Kugel vom Radius r
eingeschlossenen Teilmasse und ρ(r ) die lokale Dichte beim Abstand r ist. G ist die
Gravitationskonstante.
Hinweis: Betrachten Sie die Kräfte auf ein Volumenelement dA dr zwischen den Orten
r und r + dr.
(b) Zeigen Sie dann
dp
m (r )
= −G
.
dm
4πr4
(1 Pkt.)
(5.2)
Hinweis: Was ist dm/dr für eine Kugelschale?
(c) Zeigen Sie, dass der Ausdruck
p̃ = p +
Gm2 (r )
8πr4
(3 Pkt.)
(5.3)
eine (streng) monoton fallende Funktion von r ist. Benützen Sie das, um zu zeigen,
dass für den Druck p Z im Zentrum des Sterns gelten muss
pZ >
GM2
,
8πR4
(5.4)
wobei M und R Gesamtmasse und -radius des Sterns sind.
Hinweis: Überlegen Sie sich, dass limr→0 m(r )/r2 = 0.
(d) Der Entartungsdruck eines nichtrelativistischen Elektronengases ist
1
p=
20
Abgabe: 27. 04. 2017
2/3 2
3
h 5/3
n ,
π
me
(3 Pkt.)
(5.5)
2
Kosmologie
SS 2017
wobei me = 9.11 × 10−31 kg die Elektronenmasse und n = ρ/(me + m p ) die lokale
Anzahldichte der Elektronen ist. m p ist die (bekannte) Protonenmasse, h = 6.62 ×
10−34 Js ist das plancksche Wirkungsquantum.
Ersetzen Sie n durch die mittlere Anzahldichte des Sterns und berechnen Sie den Radius, den der Stern nicht überschreiten darf, damit der Entartungsdruck (5.5) dem
Gravitationsdruck (5.4) die Waage halten kann. Nehmen Sie zwecks Erhalt eines Zahlenwerts M = M an.
(e) Es zeigt sich, dass die benötigten Dichten so groß werden, dass die Elektronen auf- (5 Pkt.)
grund der Heisenbergschen Unschärferelation relativistische Geschwindigkeiten erreichen. Dann gilt aber nicht mehr die Zustandsgleichung (5.5) sondern stattdessen
die relativistische Gleichung
1
p=
16
1/3
3
hcn4/3 .
π
(5.6)
(Warum tritt hierin wohl die Elektronenmasse nicht mehr auf?)
Wieso kann der Stern nun den Gravitationsdruck (5.4) nicht mehr durch Verkleinerung seines Radius ausgleichen? Wie groß ist die Masse, oberhalb derer p den Wert
p Z nicht mehr erreichen kann? Wieviele Sonnenmassen M sind das? Wie verändert
sich das Ergebnis bei einer Verdopplung von p Z (was zu einer realistischeren Abschätzung des Drucks im Zentrum führt)? Unser Ergebnis ist natürlich nur eine Näherung.
Wie könnte man es im Prinzip verbessern?
Es sind insgesamt 23 Punkte zu erreichen. Die Lösungen der Aufgaben sind zum unten
genannten Termin abzugeben..
Abgabe: 27. 04. 2017
3