Aufgaben - VMP

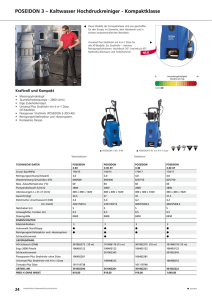
D-MATH/D-PHYS
Prof. R. Wallny
Studienjahr FS11
ETH Zürich
Klausur, Sommer 2011, Physik 2
Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus, und kreuzen Sie
Ihre Studienrichtung an. Bitte beachten Sie:
• Nicht immer hängen Teilaufgaben von den Lösungen der vorhergehenden Teilaufgaben ab!
• Die Aufgaben sind nicht nach Schwierigkeitsgrad, sondern thematisch geordnet.
• Schreiben Sie auf ALLE verwendeten Blätter (auch Notizblätter) Ihren Namen und geben Sie
sie ab.
• Bitte verwenden Sie für neue Aufgaben ein neues Blatt und kennzeichnen Sie eindeutig, an
welcher Aufgabe Sie arbeiten.
Erlaubte Hilfsmittel:
•
•
•
•
Taschenrechner: Programmierbarkeit darf nicht benutzt werden.
Mathematische Formelsammlung
Handgeschriebene Zusammenfassung, 10 A4 Seiten
Sämtliche Kommunikationsgeräte (Mobiltelephone, Laptop) sind auszuschalten und müssen
offen auf den Tisch gelegt oder in einer verschlossenen Tasche unter dem Tisch verstaut werden.
Name
Vorname
Legi-Nummer
Formelsammlung
Studienrichtung
! D-PHYS ! D-MATH ! CHAB-IN
! Andere:
Aufgabe Max.Pkt.
1
13
2
12
3
13
4
11
5
9
6
10
7
8
8
9
Total
85
Punkte
1
Visum 1
Visum 2
Aufgabe 1: Multiple Choice (13 Punkte)
a) (1 Punkt) Überprüfen Sie, dass auf der ersten Seite alle Informationen eingetragen sind: Name,
Legi-Nummer, und Studienrichtung. Bitte schreiben Sie zudem auf jedes Blatt der Klausur oben
rechts Ihren Namen.
b) (2 Punkte) Wie können Sie eine pulsförmige Störung schneller entlang einer gespannten Schnur
wandern lassen?
(a) Während Sie den Puls erzeugen, bewegen Sie Ihre Hand schneller nach oben und unten.
(b) Während Sie den Puls erzeugen, bewegen Sie Ihre Hand über eine grössere Distanz nach oben
und unten.
(c) Sie verwenden eine schwerere Schnur derselben Länge unter derselben Spannung.
(d) Sie verwenden eine leichtere Schnur derselben Länge unter derselben Spannung.
c) (2 Punkte) Eine Batterie der Spannung V ist an einen zylindrischen Drahtwiderstand der
Länge L und Querschnittsfläche A angeschlossen. Nun verdoppeln Sie die Länge L des Widerstands,
schliessen ihn aber an dieselbe Batterie an. Was passiert dann mit der Driftgeschwindigkeit (vd ) der
Elektronen in dem neuen Widerstand (verglichen mit dem kürzeren) ?
(a) vd wird kleiner
(b) vd bleibt gleich
(c) vd wird grösser
(d) unbestimmbar - nicht genug Informationen.
d) (2 Punkte) Ein Dielektrikum wird zwischen die beiden Platten eines Kondensators gebracht.
Das System wird nun mittels einer Batterie aufgeladen und anschliessend wieder von der Batterie
getrennt. Nun wird das Dielektrikum wieder entfernt. Die im Kondensator gespeicherte elektrostatische Energie ist jetzt
(a) grösser als wenn das Dielektrikum nicht entfernt worden wäre.
(b) gleich gross als wenn das Dielektrikum nicht entfernt worden wäre.
(c) kleiner als wenn das Dielektrikum nicht entfernt worden wäre.
(d) unbestimmbar - hängt von der Dielektrizitätskonstanten κ ab.
f ) (2 Punkte) Ein Elektron bewegt sich rechtwinklig zu einem magnetischen Feld. Was ist die
" ?
Richtung von B
(a) Nach links.
(b) Nach oben.
(c) Nach unten.
(d) In das Blatt hinein.
(e) Aus dem Blatt heraus.
3
e) (2 Punkte) Ordnen Sie die Potentiale Va bis Ve an den Punkten a bis e der Grösse nach, vom
grössten zum kleinsten.
(a) Va = Vb = Vc = Vd = Ve
(b) Va = Vb > Vc > Vd = Ve
(c) Vd = Ve > Vc > Va = Vb
(d) Vb = Vc = Ve > Va = Vd
(e) Va = Vb = Vd = Ve > Vc
g) (2 Punkte) Ein mit einer Glühbirne (B) verbundener Kondensator (C) wird mittels einer Batterie auf eine Anfangsladung q aufgeladen. Dann wird der Schalter S geöffnet und die Batterie
abgetrennt (siehe Bild unten).
Der Schalter S wird nun geschlossen, und der Kondensator entlädt sich über die Glühbirne. Nun
wiederholen Sie das Experiment mit Glühbirnen höherer Leistungsklassifizierung, behalten aber
dieselbe Anfangsladung q bei jedem Experiment bei. Eine Glühbirne höherer Leisungsklassifizierung
(a) brennt länger als eine Glühbirne mit tieferer Leistungsklassifizierung.
(b) brennt gleich lang wie eine Glühbirne mit tieferer Leistungsklassifizierung.
(c) brennt kürzer als eine Glühbirne mit tieferer Leistungsklassifizierung.
(d) unbestimmbar - hängt von der Spannung der Batterie ab.
4
Aufgabe 2: gekoppeltes Pendel (12 Punkte)
a) Gegeben zwei gekoppelte Pendel mit gleicher Pendellänge l und gleichen Massen m. Die beiden
Pendel seien durch eine Feder mit Federkonstante k verbunden, die an den Pendeln im Abstand d
von ihrem jeweiligen Aufhängepunkt fixiert sei. Stellen Sie die Bewegungsgleichung im Falle kleiner
Auslenkungen auf. (6 Punkte)
b) Finden Sie aus den Bewegungsgleichungen von (a) die Eigenfrequenzen und Eigenmoden. Interpretieren und skizzieren Sie diese. (6 Punkte)
Abbildung 1: Gekoppeltes Pendel gem. Aufgabenstellung
5
Aufgabe 3: “Raumschiffe” (13 Punkte)
Der Raumkreuzer Poseidon entfernt sich auf dem interstellaren Hyperspeedway von der stationären
Raumstation Neptun. Ihm kommt auf der parallel dazu verlaufenden Gegenflugbahn der Raumshuttle Artemis entgegen. Im System S der Raumstation betragen die Geschwindigkeiten der Poseidon
vp = 0.6 c und der Artemis va = −0.7 c und die Längen der Poseidon Lp = 2950 m und der Artermis
La = 125 m. Der Abstand zwischen den Flugbahnen beträgt im System der Raumstation d=10 km.
a) Bestimmen Sie die Längen La,0 und Lp,0 beider Raumschiffe, wenn sie an der Raumstation andocken um Treibstoff aufzunehmen? (2 Punkte)
b) Mit welcher Geschwindigkeit va! sieht die Crew der Poseidon die Artemis auf sich zukommen? In
welchem Abstand d’ verläuft für die Poseidon die Gegenflugbahn? (3 Punkte)
c) Berechnen Sie die Zeitspanne ∆t = t2 − t1 , die für ein Crew-Mitglied der Artemis während des
Vorbeifluges an der Poseidon vergeht. (3 Punkte)
Hinweis: Ereignis 1: Spitze von Raumschiff Artemis passiert die Spitze der Poseidon. Ereignis 2:
Spitze von Raumschiff Artemis passiert das hintere Ende der Poseidon.
d) Für Transfers zwischen Poseidon und Planeten kann ein kleines Raumshuttle der Masse ms,0
benutzt werden (ms,0 < mp,0 Masse der Poseidon ohne Shuttle). Das Raumshuttle entfernt sich
mit der Geschwindigkeit vs im ursprünglichen Ruhesystem der Poseidon (vor dem Absprengen des
Shuttles). Welche Energie Ein muss für diesen Vorgang eingebracht werden (rechnen Sie auch hier
relativistisch)? (5 Punkte)
6
Aufgabe 4: Elektrostatik (11 Punkte)
Hinweis: Die beiden Teilaufgaben können unabhängig von einander gelöst werden.
a) Ein Stück dünnen Drahtes habe die Form eines Kreisbogens des Radius R. Der Draht habe
die Länge l und trage die Ladung Q.
y
l
R
/2 /2
x
• Bestimmen Sie die Form sowie den Betrag der elektrisches Feldes im Koordinatenursprung als Funktion des Kreisbogenwinkels α = L/R. (3 Punkte)
b) Eine leitende Sphäre mit Radius R sei geerdet. Im Innern der Sphäre befinde sich eine homogene Raumladungsdichte ρ.
• Bestimmen Sie das elektrostatische Potential ϕ im Zentrum der Sphäre. (3 Punkte)
"
• Bestimmen Sie das elektrostatische Feld E(r)
für r > R. (1 Punkt)
• Berechnen Sie die elektrostatische Energie des Systems. (2 Punkte)
Stellen Sie sich nun vor, die Leiteroberfläche sei nicht geerdet und zudem trage der Leiter eine
Gesamtladung Q1 . Nehmen Sie an die Raumladungsdichte ρ(r) im Innern der Sphäre habe
die Form
ρ(r) = ρ0 r/R.
(1)
"
• Bestimmen Sie das elektrostatische Feld ausserhalb der leitenden Sphäre E(r)
für r > R.
(2 Punkte)
7
Aufgabe 5: Stromfaden (9 Punkte)
Gegeben sei ein dünner Stromfaden endlicher Leitfähigkeit σ der sich entlang der z-Achse von −L
bis +L erstreckt. Bei z = L sei das Potential als V0 gegeben. Bei z = −L ist der Stromfaden geerdet.
Effekte durch Zuleitungen sollen vernachlässigt werden.
x
V(-L)=0
-L
0
y
V(+L)
+L
z
a) Berechnen Sie das Potential V (z) im Inneren des Stromfadens. (3 Punkte)
Hinweis: Benützen Sie die Laplace Gleichung: ∆V = 0.
" im Inneren des Stromfadens. (1 Punkt)
b) Berechnen Sie die elektrische Feldstärke E
c) Wie gross ist die Stromdichte "j? (1 Punkt)
" eines dünnen Drahtes (Radius a << L) mit Stromdichte
d) Berechnen Sie das Vektorpotential A
"j für Abstände r >> a. (4 Punkte)
√
!
1
Hinweis: √ax2 +bx+c
dx = √1a ln |2ax + b + 2 ax2 + bx + c| + C.
8
Aufgabe 6: Magnetische Induktion (10 Punkte)
Zwei unendlich lange, gerade Drähte führen entgegengesetzte Ströme gleicher Intensität I(t), die
sich als Funktion der Zeit verändert. Der Abstand zwischen beiden Drähten sei d. Ausserdem liegt
eine rechtwinklige Drahtschleife mit dem Gesamtwiderstand R und den Abmessungen d × d im
Abstand d von Draht 1 entfernt (siehe Abbildung 2). Wählen Sie Ihren Koordinatenursprung auf
Draht 1.
Abbildung 2: Zwei unendlich lange Drähte und eine rechtwinklige Leiterschleife mit Widerstand R.
a) Berechnen Sie das Magnetfeld in der durch die Drähte 1 und 2 definierten Ebene. Achten Sie
dabei darauf, eine Lösung sowohl zwischen den Drähten als auch ausserhalb anzugeben. (3
Punkte)
b) Angenommen zum Zeitpunkt t = 0 werden in beiden Drähten Ströme derart angeschaltet,
dass sich für I(t) > 0 die Richtungen in Abbildung 2 ergeben. Zeichnen Sie die Richtung des
in der Leiterschleife induzierten Stromes Iind beim Einschalten auf und begründen Sie Ihre
Antwort. (2 Punkte)
c) Bestimmen Sie Iind (t) als Funktion der Zeit für t > 0, wenn sich der Strom in den unendlich
langen Drähten wie I(t) = I0 sin(ωt) verhält. (5 Punkte)
9
Aufgabe 7: Stromkreis (8 Punkte)
Betrachten Sie das abgebildete Widerstandsnetzwerk und bestimmen Sie vorzeichenrichtig das Potential am Punkt P für U1 = 6 V, U2 = 4 V und R = 100 Ω.
10
Aufgabe 8: Raumschiff mit Licht-Antrieb (9 Punkte)
Ein Raumschiff werde anhand eines Laser-Antriebs beschleunigt: Am Heck des Raumschiffs befindet sich ein Laser der eine elektromagnetische Welle entgegen der Ausbreitungsrichtung der Rakete
emittiere. Die Rakete habe eine Masse M = 10 t und befinde sich im Vakuum. Es wirke keine
Gravitation.
" = E
" 0 cos(ωt − "r"k) mit |E"0 | =
a) Die elektromagnetische Welle des Lasers habe die Form E
6
4.75 · 10 V/m. Bestimmen Sie die funktionale Form des B-Feld der elektromagnetischen Welle.
(1 Punkt)
" wobei S
" der Poyntingb) Die Intensität der elektromagnetischen Welle ist gegeben durch I := |S|,
Vektor ist:
"= 1E
" × B.
"
S
(2)
µ0
Finden Sie die zeitgemittelte Intensität < I(t) >. (3 Punkte)
" Nehmen Sie an,
c) Der Strahlungsdruck einer elektromagentischen Welle wird definiert als "π = 1c S.
2
die ebene elektromagnetische Welle werde auf einer Fläche von A = 100 cm emittiert (dies entspräche der Oberfläche der Laser-Lichtquelle). Bestimmen Sie die Beschleunigung (inclusive RIchtung)
des Raumschiffs aufgrund des Rückstosses des Strahlungsdrucks der emittierten Welle. (3 Punkte)
–
Stellen Sie sich nun vor, das Raumschiff werde nicht mit einem Laser beschleunigt sondern verfüge
über ein Sonnensegel der Fläche A! = 100 m2 . Stellen Sie sich dieses Sonnensegel als totalreflektierenden Spiegel vor, der so ausgerichtet ist, dass die Sonnenstrahlen im rechten Winkel darauf treffen.
d) Das Raumschiff befinde sich in der Entfernung von 1.5 · 108 km von der Sonne. Die Sonne emittiere eine Schwarzkörperstrahlung mit der Leistung von 3.85 · 1026 W. Wie gross ist die Intensität
der Strahlung der Sonne bei dem Raumschiff? (1 Punkt)
e) Wie gross ist die Beschleunigung des Raumschiffs aufgrund des Sonnensegels? (1 Punkt)
11