Beschreibende Statistik
Werbung

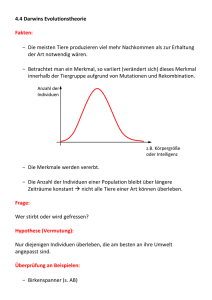
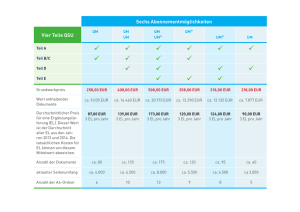
Beschreibende Statistik Daten gliedern und grafisch darstellen erhobene Daten: Urliste nominale Daten: Eigenschaften wie „Geschlecht“ oder „Wohnort“ können nicht durch eine Zahl beschrieben werden. Es gibt auch keine bestimmte Reihenfolge. Solche Daten bezeichnet man als Nominaldaten. Weitere Beispiele: Augenfarbe, Automarke, … ordinale Daten: Verschiedenen Schulabschlüsse können geordnet werden – Matura ist ein höherer Abschluss als Pflichtschule. Man kann die Rangplätze aber nicht addieren. Solche Daten heißen Ordinaldaten. Weitere Beispiele: Schulnoten, Rangplätze bei Wettbewerb, … metrische Daten: Alter und Einkommen können durch eine Zahl gemessen werden. Es ist auch sinnvoll, das Gesamteinkommen aller Mitarbeiter/innen oder die Einkommensdifferenz zweier Personen zu berechnen. Hier handelt es sich um metrische Daten. Weitere Beispiele: Größe, Gewicht, Temperatur, … Urliste der Größe nach ordnen Körpergröße Schuhgröße Wohnbezirk Geschlecht Klasseneinteilung Körpergröße Hi hi Hi hi [150; 160[ [160; 170[ [170; 180[ [180; 190[ [190; 200[ [200; 210[ Summe Schuhgröße 35 - 38 39 - 42 42 - 45 45 - 48 Summe Grafische Darstellung: Histogramm Körpergröße Schuhgröße Zentralmaße 1 1 arithmetisches Mittel (Mittelwert): ̄x = ⋅(x 1+x 2+...+xn )= ⋅∑ xi n n 1 ̄x = ⋅(x 1⋅H1 +x 2⋅H2+...)=x 1⋅h1 +x 2⋅h2 +... n nur metrische Daten, empfindlich gegenüber Ausreißern Körpergröße: Schuhgröße: Median (Zentralwert): Wert in der Mitte einer geordneten Liste sinnlos bei nominalen Daten, immun gegen Ausreißer Körpergröße: Schuhgröße: Modus (Modalwert): häufigster Wert einer Liste für nominale Daten oder wenn ein Wert sehr viel öfter auftritt Körpergröße: Schuhgröße: Wohnbezirk: Geschlecht: Streuungsmaße Standardabweichung Der Mittelwert genügt nicht, um eine statistische Verteilung zu charakterisieren. Man will auch wissen, wie stark die einzelnen Werte im Durchschnitt vom Mittelwert abweichen („wie stark sie um den Mittelwert streuen“). Auch dafür gibt es verschiedene Kennzahlen. Eine erste Idee: Man berechnet den Durchschnitt der Abweichungen vom Mittelwert, also von x i −̄x . Allerdings sind diese Werte zum Teil positiv, zum Teil negativ, und ihre Summe ergibt 0. Man berechnet daher stattdessen den Mittelwert der quadrierten Abweichungen (xi −̄x )2 , die sogenannte Varianz, und zieht daraus die Quadratwurzel. Das Ergebnis bezeichnet man als Standardabweichung σ. 1 σ= ⋅[ ( x1 −̄x )2 +(x 2−̄x )2 +...+(x n−̄ x )2 ] n √ Körpergröße: Schuhgröße: Quartile Zur Ermittlung des Medians wurde die geordnete Liste in zwei gleiche Teile geteilt. Genauso kann man sie in Viertel teilen und erhält sie sogenannten Quartile Q 1 (erstes bzw. unteres Quartil) und Q3 (drittes bzw. oberes Quartil). x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 Q1 Q2 (Median) Q3 Es gilt: Ein Viertel aller Werte ist kleiner als Q 1, drei Viertel sind größer. Drei Viertel aller Werte sind kleiner als Q3, ein Viertel ist größer. Körpergröße: Schuhgröße: Boxplot-Diagramm Körpergröße Schuhgröße