Übungen zu Experimentalphysik 2

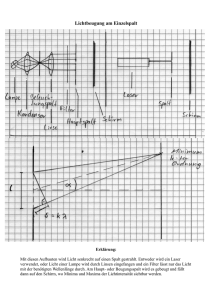
Physik Department, Technische Universität München, PD Dr. W. Schindler
Übungen zu Experimentalphysik 2
SS 13 - Lösungen zu Übungsblatt 8
1 Messung der Lichtgeschwindigkeit
(a) Zahnradmethode nach Fizeau
Licht wird durch ein Zahnrad (n Zähne, Winkelgeschwindigkeit !) auf einen Spiegel im
Abstand d geschickt und von diesem wieder zum Zahnrad zurückreflektiert. Bei genügend hohem ! hat sich das Zahnrad gerade um einen Zahn weitergedreht, das Licht
kann also zum Beobachter B gelangen. Wie kann man aus n, ! und d die Lichtgeschwindigkeit bestimmen?
Ist dieser Versuch im Hörsaal realisierbar (n = 560; d = 20 m)?
(b) Drehspiegelmethode nach Foucault
Ein Spiegel drehe sich mit der Winkelgeschwindigkeit !. Über diesen wird ein Lichtstrahl
auf einen festen Spiegel im Abstand b und von diesem wieder zurück auf den Drehspiegel
reflektiert. Da sich dieser inzwischen weitergedreht hat, wird der Strahl um s neben
die Lichtquelle reflektiert. Wie ist der Zusammenhang zwischen Lichtgeschwindigkeit c,
Winkelgeschwindigkeit !, Abstand b, dem Abstand der Messskala vom Drehspiegel a
und der Verschiebung s?
Ist dieser Versuch im Hörsaal realisierbar (a = b = 20 m; s = 1 cm)?
(a) Zahnradmethode nach Fizeau
Umlaufzeit des Zahnrades:
2⇡
!
Zeit, die die ein Zahn braucht, um die Position eines anderen Zahnes zu erreichen:
T =
t=
T
2⇡
=
n
n!
In dieser Zeit läuft der Strahl den Weg
l = 2d.
1
Die Lichtgeschwindigkeit ergibt sich zu:
2dn!
dn!
=
.
t
2⇡
⇡
Für das Experiment benötigt man damit eine Winkelgeschwindigkeit von
c=
l
=
c⇡
1
1
= 84 · 103 = 84
.
dn
s
ms
Dies ist sehr schnell für einen Hörsaalversuch.
(b) Drehspiegelmethode nach Foucault
Der Strahlweg vom rotierenden zum festen Spiegel und zurück ist
! =
l = 2b.
Die Zeit, die das Licht für diesen Weg braucht ist
l
2b
= .
c
c
In dieser Zeit dreht sich der Spiegel um den Winkel
t=
2b!
.
c
Der Strahl wird bei der Reflexion vom rotierenden Spiegel um
= t! =
4b!
c
abgelenkt. Die Ablenkung am Schirm beträgt somit
2 =
4b!
.
c
Für diesen Versuch benötigt man somit eine Winkelgeschwindigkeit von
s = a tan (2 ) ⇡ a2 = a
c s
1
1
= 1.8 · 103 = 1.8
.
4ab
s
ms
Diese ist schon eher realisierbar.
!=
2 Michelson-Interferometer
2
Bei dem abgebildeten Interferometer beobachtet man nacheinander 10 Interferenzmaxima,
wenn man einen der beiden Spiegel um eine Strecke von 2.25 µm in Strahlrichtung verschiebt.
(a) Bestimmen Sie die Wellenlänge des Lichts.
(Tipp: Betrachten Sie den Zusammenhang zwischen Gangunterschied der zwei Lichtwege und der Bedingung für Interferenzmaxima.)
(b) Zwischen einen der Spiegel und den Strahlteiler wird nun eine mit CO2 -Gas gefüllte Zelle
(Länge L = 10 cm) gestellt. Beim Abpumpen der Zelle werden 200 Interferenzmaxima
beobachtet. Welchen Brechungsindex n hat das CO2 -Gas, wenn sich der restliche Aufbau im Vakuum befindet?
(Hinweis: Bedenken Sie, dass die Lichtgeschwindigkeit im Gas um den Faktor n kleiner
ist als im Vakuum, also c = c0 /n und damit auch die Wellenberge der Lichtwelle um
den Faktor n näher zusammenrücken.)
(a) Für den Fall, dass der Spiegel um d = 2.25 µm verschoben ist, beträgt der Gangunterschied zwischen den zwei Lichtwegen:
l = 2d = 4.5 · 10
6
m.
Im allgemeinen beobachtet man ein Maximum, wenn der Gangunterschied ein ganzzahliges Vielfaches k der Wellenlänge ist:
l=k .
Beim Verfahren des Spiegels wurden 10 Interferenzmaxima beobachtet, d. h. k = 10
und somit:
=
l
k
= 450 · 10
9
m = 450 nm
(b) Es entsteht ein Gangunterschied durch das eingebrachte Medium (Länge L = 10 cm).
Dadurch, dass die elektromagnetische Welle im Gas um den Faktor n gestaucht ist,
verhält sie sich, als hätte sie einen n-mal längeren Weg im Vakuum zurückgelegt (diese
Größe heißt auch optische Weglänge):
l = nL.
Der Unterschied in der optischen Weglänge mit Gas und ohne Gas beträgt:
l = l2
l1 = 2nL
2L = 2L (n
1) .
Man beobachtet ein Maximum, wenn
l=k .
Einsetzen von
l ergibt:
2L (n
1) = k
Beim Abpumpen wurden 200 Interferenzmaxima beobachtet, d. h. k = 200. Somit ist:
n=1+
k
= 1.00045
2L
3
3 Doppelspalt
Auf einen Doppelspalt trifft Licht der Wellenlänge . Die Öffnungen sind wesentlich kleiner
als ihr Abstand d (siehe Abb.).
(a) Stellen Sie anhand der Abbildung eine
Gleichung für den Gangunterschied s
der beiden Strahlen auf.
(b) Unter welchen Winkeln führt der Gangunterschied zu Minima und unter welchen
zu Maxima?
Auf einem Schirm in 30 cm Entfernung vom Doppelspalt beobachtet man zwei benachbarte
Maxima 6.4244 cm und 8.7229 cm entfernt vom Maximum 0. Ordnung.
(c) Unter welchen Winkeln ↵A und ↵B entstehen die Beugungsmaxima?
(d) Welcher Ordnung nA und nB entspricht das?
Die Wellenlänge des eingestrahlten Lichts beträgt
(e) Wie groß ist der Spaltabstand d?
= 689 nm.
(a)
s = d sin (↵)
(b)
Maxima ergeben sich bei:
s = n , mit n = 0, 1 2, ...
(der Gangunterschied entspricht einem ganzzahligen Vielfachen der Wellenlänge
des Lichts)
Minima ergeben sich bei:
✓
◆
1
s= n+
, mit n = 0, 1 2, ...
2
(c)
✓
◆
6.4244 cm
↵A = arctan
= 12.087
30 cm
✓
◆
8.7229 cm
↵B = arctan
= 16.213
30 cm
(d)
nA
sin (↵A )
3
=
= 0.75 =
nB
sin (↵B )
4
(e)
) Maxima der 3. und 4. Ordnung
d=
nA
= 9.87 µm
sin (↵A )
4