Folien zu Logik
Werbung

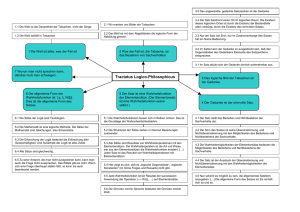
Mathematik und Logik Aussagen 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Die mathematische Logik verwendet mathematische Methoden, um das logische Denken formal zu beschreiben. I Populäre Definition: Eine Aussage ist ein Satz, der entweder falsch oder wahr ist. I Problem: Wie definiert man wahr und falsch? I Ein Beweis stellt sicher, daß eine Aussage wahr ist. I Definition: Eine Aussage ist eine Konstruktion, durch welche festgelegt wird, wie ihre Beweise zu konstruieren sind. I Eine Aussage, die wir nicht beweisen können, muß nicht unbedingt falsch sein. Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Mathematik und Logik Definition der Implikation, ⇒ 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Formation Sind P und Q Aussagen, dann bezeichnet P ⇒ Q ebenfalls eine Aussage, die Implikation von P und Q. Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Introduktion Um P ⇒ Q zu beweisen, muß man Q beweisen, wobei man einen Beweis von P voraussetzen darf. Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Elimination Hat man einen Beweis von P ⇒ Q, so reicht ein Beweis von P, um auch Q zu beweisen. Schlußregeln P Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra .. . Q P⇒Q ⇒I P⇒Q Q P ⇒E Mathematik und Logik Definition der Konjuktion, ∧ 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Formation Sind P und Q Aussagen, dann bezeichnet P ∧ Q ebenfalls eine Aussage, die Konjunktion von P und Q. Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen Introduktion Um P ∧ Q zu beweisen, muß man sowohl P als auch Q beweisen. RSA-Verschlüsselung Logik Elimination Aussagenlogik Hat man einen Beweis von P ∧ Q so auch einen Beweis von P, und auch einen Beweis von Q. Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Schlußregeln Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra P Q ∧I P ∧ Q P ∧ Q ∧E0 P P ∧ Q ∧E1 Q Mathematik und Logik Kommutativität der Konjunktion 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Satz Die logische Konjunktion ist kommutativ, d.h. die Aussage Teilbarkeit Gemeinsame Teiler A ∧ B⇒B ∧ A Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen ist allgemeingültig. RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Beweis. A ∧ B A ∧ B A ∧ B ∧E1 ∧E0 B A ∧I B ∧ A A ∧ B⇒B ∧ A ⇒I Mathematik und Logik Definition der Äquivalenz, ⇐⇒ 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Notation Die logische Äquivalenz wird mit P ⇐⇒ Q bezeichnet und ist lediglich eine Abkürzung für (P ⇒ Q) ∧ (Q ⇒ P). Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Bemerkung Zwei Aussagen sind äquivalent wenn sie vom logischen Standpunkt aus betrachtet gleichwertig sind. Mathematik und Logik Definition der Disjunktion, ∨ 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Formation Sind P und Q Aussagen, dann bezeichnet P ∨ Q ebenfalls eine Aussage, die Disjunktion von P und Q. Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Introduktion Um P ∨ Q zu beweisen, genügt es, P zu beweisen, oder Q zu beweisen. Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Elimination Folgt irgendeine Aussage R sowohl aus P als auch aus Q, dann folgt sie auch aus P ∨ Q (Beweis durch Fallunterscheidung). Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Schlußregeln P ∨I0 P ∨ Q Q ∨I1 P ∨ Q P⇒R Q⇒R ∨E P ∨ Q R Mathematik und Logik Allquantor, ∀ 2011W Was ist Logik? I Sei X ein Datentyp, und P[x] für jedes x X eine Aussage. Dann bezeichnet ∀xX P[x] eine All-Aussage. I Die All-Aussage drückt eine universelle Quantifizierung aus. I Ein Beweis von ∀xX P[x] konstruiert für jedes beliebige x X einen Beweis von P[x]. I Praktisch: Es sei ∀xX P[x] zu beweisen. Vorgangsweise: Annahme x X ; beweise P[x]. I Hängt P[x] nicht von x ab, dann liegt eine normale Implikation vor: ∀xX P ist dasselbe wie X → P. Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Mathematik und Logik Allquantor, Introduktion und Elimination 2011W Was ist Logik? I Um ∀xX P[x] zu beweisen, muß man P[x] für ein beliebiges x X beweisen. I ∀-Introduktion: Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Gemeinsame Teiler Diophantische Gleichungen xX .. . Teilerfremde Zahlen Modulare Arithmetik Primzahlen P[x] RSA-Verschlüsselung Logik ∀xX P[x] Aussagenlogik ∀I Logische Implikation, ⇒ Logische Konjunktion, ∧ I Wurde ∀xX P[x] bewiesen, und ist a X , dann hat man einen Beweis von P[a]. I ∀-Elimination: Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra ∀xX P[x] a X ∀E P[a] Mathematik und Logik Allquantor, Beispiel 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit ∀xX A[x] ∨ ∀yY B[y] Gemeinsame Teiler Diophantische Gleichungen xX Teilerfremde Zahlen Modulare Arithmetik Primzahlen yY RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ .. . A[x] ∨ B[y] ∀I ∀yY (A[x] ∨ B[y]) Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra ∀xX ∀yY (A[x] ∨ B[y]) ∀I ⇒I ∀xX A[x] ∨ ∀yY B[y] ⇒ ∀xX ∀yY (A[x] ∨ B[y]) Mathematik und Logik Allquantor: Beispiel (Fortsetzung) 2011W Was ist Logik? Elementare Zahlentheorie Annahmen: ∀xX A[x] ∨ ∀yY B[y], Zu beweisen: x X, yY Natürliche Zahlen Teilbarkeit ∀xX A[x] ∀yY B[y] .. . .. . A[x] ∨ B[y] A[x] ∨ B[y] Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Logik ∀xX A[x] ∨ ∀yY B[y] ⇒ A[x] ∨ B[y] ∨E Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Die beiden Fälle: ∀xX A[x] x X ∀E A[x] ∨I0 A[x] ∨ B[y] ∀yY B[y] y Y ∀E B[y] ∨I1 A[x] ∨ B[y] Mathematik und Logik Existenzquantor, ∃ 2011W Was ist Logik? I Sei X ein Datentyp, und P[x] für jedes x X eine Aussage. Dann bezeichnet ∃xX P[x] eine Existenz-Aussage. I Die Existenzaussage drückt eine existenzielle Quantifizierung aus. I Ein Beweis von ∃xX P[x] konstruiert ein a X und einen Beweis von P[a]. I Praktisch: Es sei ∃xX P[x] zu beweisen. Vorgangsweise: Man wählt ein passendes a X , und versucht damit P[a] zu beweisen. I Hängt P[x] nicht von x ab, dann liegt eine normale Konjunktion vor: ∃xX P ist dasselbe wie X ∧ P. Elementare Zahlentheorie Natürliche Zahlen Teilbarkeit Gemeinsame Teiler Diophantische Gleichungen Teilerfremde Zahlen Modulare Arithmetik Primzahlen RSA-Verschlüsselung Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Äquivalenz, ⇐⇒ Logische Disjunktion, ∨ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra Mathematik und Logik 2011W Was ist Logik? Elementare Zahlentheorie Natürliche Zahlen Existenzquantor: Introduktion und Elimination I Teilbarkeit Gemeinsame Teiler Diophantische Gleichungen I Teilerfremde Zahlen Modulare Arithmetik Um ∃xX P[x] zu beweisen, muß man ein a X finden und damit P[a] beweisen. a X P[a] ∃-Introduktion: ∃I ∃xX P[x] Primzahlen RSA-Verschlüsselung I Wurde ∃xX P[x] bewiesen, so kann man für’s weitere annehmen, daß es ein soches Objekt gibt. I ∃-Elimination: Logik Aussagenlogik Logische Implikation, ⇒ Logische Konjunktion, ∧ yX Logische Äquivalenz, ⇐⇒ Prädikatenlogik Allquantor, ∀ Existenzquantor, ∃ Datentypen Logische Implikation, ⇒ Logische Konjunktion, ∧ Logische Disjunktion, ∨ Curry-HowardIsomorphismus Listen Lineare Algebra P[y] .. . Logische Disjunktion, ∨ Q ∃xX P[x] Q ∃E