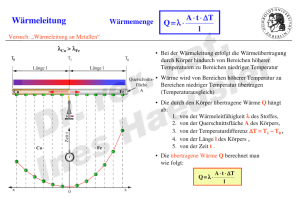
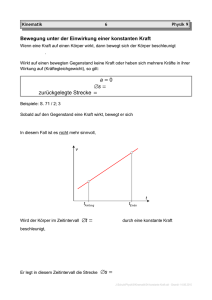
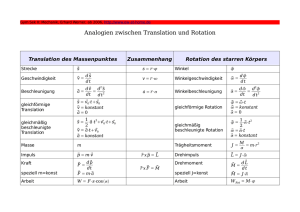
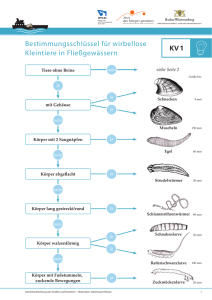
Kinematik des starren Körpers

Kinematik des starren Körpers
●
●
●
12.02.15
Ein starrer Körper ist eine Idealisierung für einen realen
Körper, dessen Verformungen so klein sind, dass sie vernachlässigt werden können.
Ein starrer Körper kann als ein System von unendlich vielen Massenpunkten aufgefasst werden, deren gegenseitige Abstände sich nicht ändern. Zwischen den Massenpunkten liegen starre Bindungen vor.
Folgende Annahme wird getroffen:
–
Bei einer beliebigen Bewegung des Körpers ändert sich der
Abstand zwischen zwei beliebig herausgegriffenen Punkten
auf dem Körper nicht.
Prof. Dr. Wandinger
3. Kinematik des starren Körpers
TM 3 3-1
12.02.15
Kinematik des starren Körpers
●
Folgerung:
–
Werden drei Punkte auf dem Körper markiert, so ändern
sich die Seitenlängen des dadurch definierten Dreiecks
nicht.
–
Daher ändern sich die Winkel zwischen den Seiten nicht.
–
Bei einer beliebigen Bewegung eines starren Körpers ändert sich der Winkel zwischen zwei beliebigen sich schneidenden Linien auf dem Körper nicht.
–
Aus der Mathematik folgt, dass sich die Bewegung des starren Körpers aus einer Translation und einer Rotation zusammensetzt.
Prof. Dr. Wandinger
3. Kinematik des starren Körpers
TM 3 3-2
12.02.15
Kinematik des starren Körpers
C
C
γ
γ
β
a
b
A
Prof. Dr. Wandinger
B
b
β
α
a
c
B
α
c
A
3. Kinematik des starren Körpers
TM 3 3-3
Kinematik des starren Körpers
12.02.15
1. Grundlagen der ebenen Kinematik
2. Momentanpol
3. Analytische Kinematik
Prof. Dr. Wandinger
3. Kinematik des starren Körpers
TM 3 3-4