Fach: Mathematik / Geometrie Planung für das 7. Schuljahr
Werbung
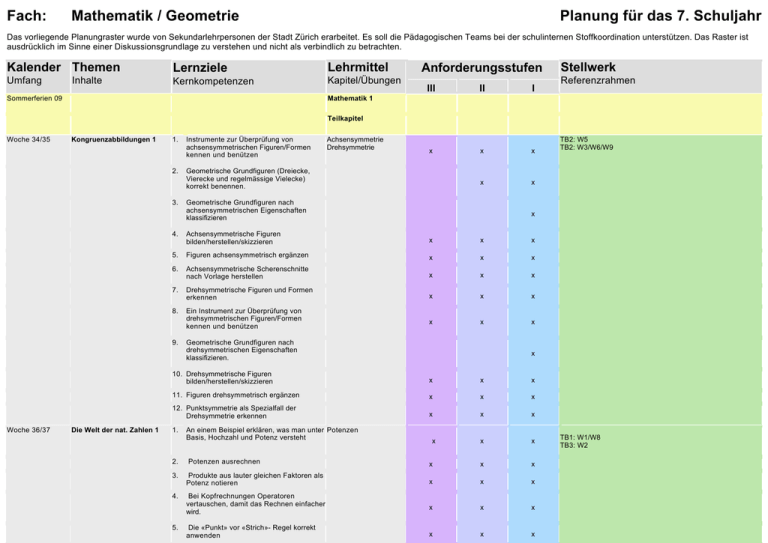
Fach: Mathematik / Geometrie Planung für das 7. Schuljahr Das vorliegende Planungraster wurde von Sekundarlehrpersonen der Stadt Zürich erarbeitet. Es soll die Pädagogischen Teams bei der schulinternen Stoffkoordination unterstützen. Das Raster ist ausdrücklich im Sinne einer Diskussionsgrundlage zu verstehen und nicht als verbindlich zu betrachten. Kalender Themen Umfang Inhalte Lernziele Kernkompetenzen Lehrmittel Kapitel/Übungen Mathematik 1 Sommerferien 09 Anforderungsstufen III II I Stellwerk Referenzrahmen Teilkapitel Woche 34/35 Kongruenzabbildungen 1 1. 2. 3. Die Welt der nat. Zahlen 1 Achsensymmetrie Drehsymmetrie x Geometrische Grundfiguren (Dreiecke, Vierecke und regelmässige Vielecke) korrekt benennen. x x x x Geometrische Grundfiguren nach achsensymmetrischen Eigenschaften klassifizieren Achsensymmetrische Figuren bilden/herstellen/skizzieren x x x 5. Figuren achsensymmetrisch ergänzen x x x 6. Achsensymmetrische Scherenschnitte nach Vorlage herstellen x x x 7. Drehsymmetrische Figuren und Formen erkennen x x x 8. Ein Instrument zur Überprüfung von drehsymmetrischen Figuren/Formen kennen und benützen x x x Geometrische Grundfiguren nach drehsymmetrischen Eigenschaften klassifizieren. x 10. Drehsymmetrische Figuren bilden/herstellen/skizzieren x x x 11. Figuren drehsymmetrisch ergänzen x x x 12. Punktsymmetrie als Spezialfall der Drehsymmetrie erkennen x x x x x 1. An einem Beispiel erklären, was man unter Potenzen Basis, Hochzahl und Potenz versteht x 2. Potenzen ausrechnen x x x 3. Produkte aus lauter gleichen Faktoren als Potenz notieren x x x 4. Bei Kopfrechnungen Operatoren vertauschen, damit das Rechnen einfacher wird. x x x x x x 5. Die «Punkt» vor «Strich»- Regel korrekt anwenden TB2: W5 TB2: W3/W6/W9 x 4. 9. Woche 36/37 Instrumente zur Überprüfung von achsensymmetrischen Figuren/Formen kennen und benützen TB1: W1/W8 TB3: W2 6. Mit Worten formulierte Rechnungen als Terme notieren 7. Einfache Terme unter Verwendung der Fachbegriffe mit Worten beschreiben 8. Bei Termumformungen angeben, welches der drei Gesetze (Assoziativ-, Kommutativoder Distributiv-Gesetz) jeweils zur Anwendung kommt 9. x x x x x x Mit Klammern angegebene Summen oder Differenzen in Termen subtrahieren x x x 10. In Termen mit geklammerten Produkten oder Quotienten dividieren x x x 11. Auf einem Zahlenstrahl Potenzen markieren x x x x x x 12. Ein Zahlengitter mit zwei additiven oder zwei multiplikativen Operatoren korrekt ausfüllen, d.h. auch die Eintragungen im Gitter selber überprüfen 13. Begründen, warum bei einem Zahlengitter additive und multiplikative Operatoren nicht gemischt auftreten können. x 14. Eine bis zu 22stellige natürliche Zahl korrekt lesen x x x x x x x x x x x x In einem Term für die Variable(n) Zahlenwert einsetzen und den Wert des Term bestimmen x x x Die Schilderung eines Lösungsvorgehens beim «100er Spiel» verstehen und nachvollziehen x x x x x x x 15. Die Anzeige im Taschenrechner einer mehr als 15stelligen natürlichen Zahl richtig herausschreiben und ohne Zehnerpotenz notieren können 1. Woche 38 2. 3. 4. 5. 6. 7. Woche 39/40 Kongruenzabbildungen 2 1. Für einen (einfachen) Sachverhalt, der in einem Text vorliegt, einen Term mit einer Variablen aufsetzen Variablen Für einen (einfachen) Sachverhalt, der in einem Text vorliegt, einen Term mit zwei Variablen aufsetzen Ein durch ein Beispiel gegebenes Lösungsvorgehen beim «100er-Spiel» an einem anderen Zahlenbeispiel vorführen Einem vorgegebenen einfachen Term einen gegebenen Sachverhalt zuordnen und umgekehrt Die mathematischen Fachausdrücke beim Beschreiben eines Terms benützen Eigenschaften der Achsenspiegelung x Achsenspiegelung TB2: W1/W4/W9 benennen. x x x Original- und Bildfigur zusammen als achsensymmetrische Gesamtfigur erkennen x x x 3. Punkt oder Figur an der Spiegelachse spiegeln. x x x 4. Grundkonstruktionen ausführen können (Mittelsenkrechte, Winkelhalbierende, Mittelparallele. x x x 5. Spiegelachse anhand von Original- und Bildfigur konstruieren. x x x 6. Bild- und/oder Originalfigur ergänzen x x 7. Basisfigur in achsensymmetrischen Figuren identifizieren 2. Herbstferien Woche 43 Woche 44/45 Kongruenzabbildungen 2 Die Welt der nat. Zahlen 2 1. Eigenschaften der Punktspiegelung benennen 2. x Punktspiegelung x x x Punkt oder Figur am Spiegelzentrum spiegeln x x x 3. Spiegelzentrum anhand von Originalund Bildfigur konstruieren x x x 4. Bild- und/oder Originalfigur ergänzen x x 5. Zusammenhang Achsenspieglung/Punktspiegelung erkennen TB2: W5/W9 x 1. Entscheiden, ob eine bestimmte Zahl Teiler ist einer anderen Zahl 2. Entscheiden, ob eine bestimmte Zahl Vielfaches ist einer anderen Zahl x x x 3. Bei einer Multiplikation wie z.B. 3x4 = 12 erklären, welche Zahl von welcher anderen Teiler, respektive Vielfaches ist x x x 4. Eine natürliche Zahl in ihre Primfaktoren zerlegen x x x 5. Die Primfaktorenzerlegung einer natürlichen Zahl auch mit Potenzen angeben x x x x Teiler, Vielfache, Primzahlen x x x 6. Beschreiben, wann eine natürliche Zahl Primzahl ist 7. Die Primzahlen zwischen 1 und 20 aufzählen x x 8. Systematisch alle Teiler einer natürlichen Zahl bestimmen x x 9. Beschreiben, welche natürlichen Zahlen eine gerade und welche eine ungerade Anzahl Teiler aufweisen x x x 10. Beschreiben, welche natürliche Zahlen genau zwei Teiler aufweisen x x x 11. Beschreiben, was man unter einer «armen», einer «vollkommenen» und einer «reichen» natürlichen Zahl versteht x x x TB1: W8 12. Herausfinden, ob eine natürliche Zahl «arm», «vollkommen» oder «reich» ist 13. Für Zahlen mit weniger als 3 Primfaktoren, mit Hilfe eines Zahlengitters alle Teiler bestimmen x x x 15. Für Zahlen mit 3 Primfaktoren, mit Hilfe eines Zahlengitters alle Teiler bestimmen x 16. Beschreiben, was man unter dem ggT und dem kgV zweier Zahlen versteht x 17. Den ggT und das kgV zweier Zahlen mit Hilfe eines Zahlengitters bestimmen x Daten und Grössen Umstufungstermin: Beginn in neuer Anforderungsstufe Woche 49 x x x 19. Mit Hilfe des Produkts zweier natürlichen Zahlen aus dem ggT deren kgV bestimmen und umgekehrt. Woche 47/48 x 14. Für Zahlen mit 3 Primfaktoren, mit Hilfe eines Zahlengitters alle Teiler bestimmen 18. Den ggT und das kgV zweier Zahlen aus deren Primfaktorenzerlegung bestimmen Woche 46 x x Daten darstellen TB1: W3/W4/W18 TB4: W1/W2/W3/W4/W7 Längen, Gewicht, Hohlmasse, Zeit TB1: W9/W10/W11/ W11/W16 1. Ich weiss, voraus Grössen bestehen (Zahlwert, Einheit). 2. Ich kenne die Einheiten für Längen-, Flächen-, Volumen-, für Hohl-, und Gewichtsmasse. 3. Ich kenne die Brücke zwischen Volumen-, für Hohl-, und Gewichtsmasse. 4. Ich kann Flächen- in Raummasse verwandeln. 5. Ich weiss, was die Basiseinheit ist. 6. Ich weiss, dass der Quadratmeter eine abgeleitete Einheit darstellt. 7. Ich kenne die Einheiten für Zeit und Winkelmessung. 8. Ich kann nichtdezimale Grössen addieren und subtrahieren. 1. Ich kann Einheitsquadrate im Quadratgitter Flächen und Volumen auszählen. 2. Ich weiss, was ein Flächeninhalt ist. 3. Ich weiss, was man unter einer Grundseite versteht. 4. Ich kann Dreiecks- Flächeninhalte berechnen: Allgemein: Dreieck als halbes Rechteck Spezialfälle: Rechtwinklig, rechtwinkliggleichschenklig TB1: W12/W13/W14/W15 5. Ich kann Formel und deren Umkehrungen einsetzen 6. Ich kenne die Begriffe: Vieleck, Parallelenviereck, Rhomboid, Rhombus, Diagonale 7. Ich kann Flächeninhalte von Vielecken (Parallelenviereck, Rhombus, n-Eck) berechnen 8. Ich kann Flächen von zusammengesetzten Figuren berechnen unter Verwendung bekannter Gesetzmässigkeiten: Symmetrieeigenschaften, Winkelbeziehungen, Thaleskreis, Formel zur Berechnung von Dreiecken, Parallelenvierecke sowie Rhomben. Volumen: Woche 50 Weihnachtsferien Körper und ihr Aufbau 1. Ich kenne den Unterschied eines Würfels und eines Quaders. 2. Ich kann das Volumen, den Rauminhalt und den Oberflächeninhalt von einem Würfel und von einem Quader berechnen. 3. Ich kann mit diesen Grössen (Volumen und Oberfläche) durch Umkehrüberlegungen operieren und kann diesen Sachzusammenhang formal darstellen. 4. Ich kann das Volumen und den Oberflächeninhalt von Körpern berechnen, die aus Quadern zusammengesetzt werden können. 1. Ich kenne und verstehe die Begriffe Netz und Oberfläche 2. Ich kann Schrägbilder in Netze und umgekehrt übertragen 3. Ich kann mir die Bewegung von Körpern im Raum vorstellen. 4. Ich kann einen Quader darstellen und kenne seine Eigenschaften. 5. Ich kenne die Begriffe Grund- und Deckfläche, Seitenfläche, Mantel und Netz eines Quaders und kann sie richtig zuordnen. 6. Ich kann ein Quadernetz konstruieren. Körper und ihre Netze keine Übereinstimmung











