Grundwissen Geometrie

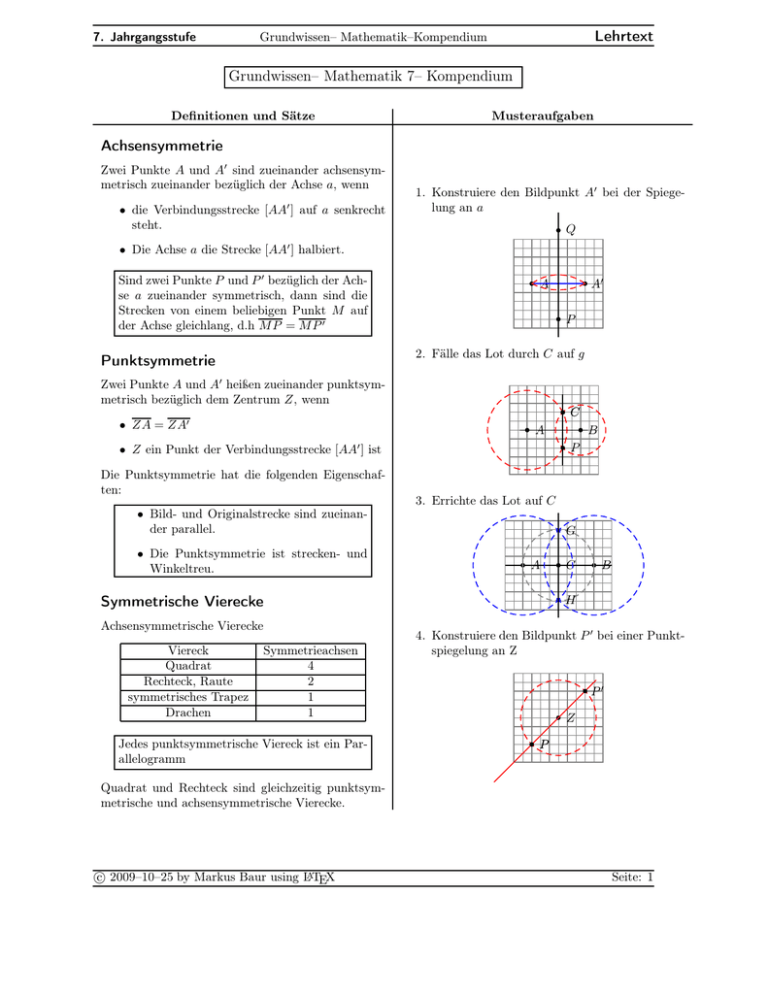
7. Jahrgangsstufe
Lehrtext
Grundwissen– Mathematik–Kompendium
Grundwissen– Mathematik 7– Kompendium
Definitionen und Sätze
Musteraufgaben
Achsensymmetrie
Zwei Punkte A und A′ sind zueinander achsensymmetrisch zueinander bezüglich der Achse a, wenn
′
• die Verbindungsstrecke [AA ] auf a senkrecht
steht.
1. Konstruiere den Bildpunkt A′ bei der Spiegelung an a
Q
b
′
• Die Achse a die Strecke [AA ] halbiert.
Sind zwei Punkte P und P ′ bezüglich der Achse a zueinander symmetrisch, dann sind die
Strecken von einem beliebigen Punkt M auf
der Achse gleichlang, d.h M P = M P ′
b
A
b
A′
P
b
2. Fälle das Lot durch C auf g
Punktsymmetrie
Zwei Punkte A und A′ heißen zueinander punktsymmetrisch bezüglich dem Zentrum Z, wenn
b
• ZA = ZA′
b
• Z ein Punkt der Verbindungsstrecke [AA ] ist
Viereck
Quadrat
Rechteck, Raute
symmetrisches Trapez
Drachen
G
b
b
A
b
Symmetrische Vierecke
b
Achsensymmetrische Vierecke
Symmetrieachsen
4
2
1
1
Jedes punktsymmetrische Viereck ist ein Parallelogramm
P
3. Errichte das Lot auf C
• Bild- und Originalstrecke sind zueinander parallel.
• Die Punktsymmetrie ist strecken- und
Winkeltreu.
B
b
′
Die Punktsymmetrie hat die folgenden Eigenschaften:
C
A
b
C
b
B
H
4. Konstruiere den Bildpunkt P ′ bei einer Punktspiegelung an Z
b
b
b
P′
Z
P
Quadrat und Rechteck sind gleichzeitig punktsymmetrische und achsensymmetrische Vierecke.
c 2009–10–25 by Markus Baur using LATEX
Seite: 1
7. Jahrgangsstufe
Grundwissen– Mathematik–Kompendium
c 2009–10–25 by Markus Baur using LATEX
Lehrtext
Seite: 2
7. Jahrgangsstufe
Lehrtext
Grundwissen– Mathematik–Kompendium
Definitionen und Sätze
Musteraufgaben
Winkelgesetze
Winkel an der Geradenkreuzung
• Scheitelwinkel, die sich gegenüberliegen: α, β
1. In der folgenden auf der linken Seite abgebildeten Doppelkreuzung gilt AB||AC. Der Winkel α = 70◦ . Berechne die Winkel β, γ und ϕ.
Begründe dabei die einzelnen Schritte mit den
Winkelgesetzen.
• Nebenwinkel α, γ
B
b
C β
α
Sγ
b
b
A
b
b
D
δ = α = 70◦ (Stufenwinkel)
Werden zwei Parallelen von einer weiteren Gerade
geschnitten, dann gelten die folgenden die Gesetzmäßigkeiten:
β = 180◦ − 70◦ = 110◦ (Nebenwinkel)
γ = β = 110◦ (Nebenbwinkel)
ϕ = 180◦ − δ = 110◦
E
b
δ
b
Cβ
α S
γ
A
b
ϕ
2. In einem Dreieck ist der erste Winkel halb so
groß wie der zweite Winkel und der dritte Winkel ist doppelt so groß wie der zweite Winkel:
Berechne die Größen der drei Innenwinkel des
Dreiecks:
B
b
b
D
b
G
b
• Stufenwinkel sind gleich groß:
α + β + γ = 180◦
α=δ
0,5 β + β + 2 β = 180◦
3,5β = 180◦
• Wechselwinkel sind gleich groß:
β = 51,4◦
β=ϕ
• Nachbarwinkel ergänzen sich zu 180◦
δ + β = 180◦
3. In einem Viereck ist jeder Winkel doppelt so
groß wie der nächste. Berechne die Größe des
ersten Winkels:
α+β +γ +δ = 360◦ (Winkelsumme im Viereck)
Innenwinkelsumme Dreieck:
C
α + 2α + 4α + 8α = 360◦
b
15α = 360◦
γ
α
b
α = 24◦
β
A
b
B
α + β + γ = 180◦
c 2009–10–25 by Markus Baur using LATEX
Seite: 3